Turunan dari Fungsi Daya dari e

Contoh Turunan dari e

Konstanta Proporsionalitas

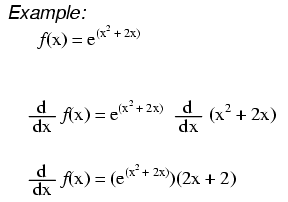
Ketika kita mengatakan bahwa suatu hubungan atau fenomena adalah "eksponensial", kita menyiratkan bahwa beberapa kuantitas—arus listrik, keuntungan, populasi—meningkat lebih cepat seiring dengan bertambahnya kuantitas. Dengan kata lain, laju perubahan terhadap variabel tertentu sebanding dengan nilai variabel itu. Ini berarti bahwa turunan dari fungsi eksponensial sama dengan fungsi eksponensial asli dikalikan dengan konstanta (k ) yang membentuk proporsionalitas.

$$\frac{\text{d}}{\text{d}x}a^x=ka^x$$

Konstanta proporsionalitas sama dengan log natural dari basis eksponen:

$$\frac{\text{d}}{\text{d}x}a^x=\ln(a)\times a^x$$

Oleh karena itu, jika log natural dari basis sama dengan satu, turunan dari fungsi tersebut akan sama dengan fungsi aslinya. Inilah yang terjadi dengan fungsi pangkat dari e:log natural dari e adalah 1, dan akibatnya, turunan dari $$e^x$$ adalah $$e^x$$.

$$\frac{\text{d}}{\text{d}x}e^x=e^x$$

Aturan "Rantai"

Ketika ekspresi eksponensial adalah sesuatu selain x, kita menerapkan aturan rantai:Pertama kita ambil turunan dari seluruh ekspresi, lalu kita kalikan dengan turunan dari ekspresi dalam eksponen.

$$\frac{\text{d}}{\text{d}x}e^{x^2+2x}=e^{x^2+2x}\times\frac{\text{d}}{ \text{d}x}(x^2+2x)=(2x+2)e^{x^2+2x}$$

Teknik ini dapat digunakan untuk mencari laju perubahan arus dioda terhadap tegangan dioda. Persamaan berikut memberikan perkiraan hubungan antara tegangan melintasi dioda ($$V_D$$) dan arus yang melalui dioda ($$I_D$$):

$$I_D=I_S\times e^\frac{V_D}{0.026}$$

(Lihat halaman dioda dan penyearah untuk informasi lebih lanjut tentang persamaan arus-tegangan dioda; juga, perhatikan bahwa $$I_S$$ adalah konstanta, bukan variabel.) Untuk menemukan laju perubahan arus terhadap tegangan, kita ambil turunannya:

$$\frac{\text{d}I_D}{\text{d}V_D}=\frac{\text{d}}{\text{d}V_D}(I_S\times e^\frac{V_D}{ 0.026})=I_S\times e^\frac{V_D}{0.026}\times\frac{1}{0.026}$$

Jadi, pada nilai tegangan dioda tertentu $$V_D$$, peningkatan tegangan akan menghasilkan peningkatan arus sebesar $$\frac{I_S}{0.026}e^\frac{V_D}{0.026}$$ .

LEMBAR KERJA TERKAIT:

• Lembar Kerja Kalkulus untuk Rangkaian Listrik