MATLAB - Kalkulus

MATLAB menyediakan berbagai cara untuk menyelesaikan masalah kalkulus diferensial dan integral, memecahkan persamaan diferensial dari berbagai derajat dan perhitungan batas. Yang terbaik dari semuanya, Anda dapat dengan mudah memplot grafik fungsi kompleks dan memeriksa maksimum, minimum, dan titik alat tulis lainnya pada grafik dengan menyelesaikan fungsi asli, serta turunannya.

Bab ini akan membahas masalah kalkulus. Dalam bab ini, kita akan membahas konsep pra-kalkulus yaitu menghitung limit fungsi dan memverifikasi sifat limit.

Di bab berikutnya Diferensial , kita akan menghitung turunan dari suatu ekspresi dan menemukan maxima dan minima lokal pada grafik. Kami juga akan membahas penyelesaian persamaan diferensial.

Akhirnya, dalam Integrasi bab, kita akan membahas kalkulus integral.

Menghitung Batas

MATLAB memberikan batas fungsi untuk menghitung limit. Dalam bentuknya yang paling dasar, batas fungsi mengambil ekspresi sebagai argumen dan menemukan batas ekspresi saat variabel independen menjadi nol.

Sebagai contoh, mari kita hitung limit suatu fungsi f(x) =(x ³ + 5)/(x ⁴ + 7), karena x cenderung nol.

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut

ans =
   5/7

Fungsi limit termasuk dalam ranah komputasi simbolik; anda perlu menggunakan syms berfungsi untuk memberi tahu MATLAB variabel simbolis mana yang Anda gunakan. Anda juga dapat menghitung limit suatu fungsi, karena variabel cenderung ke beberapa angka selain nol. Untuk menghitung lim _x->a (f(x)), kita menggunakan perintah limit dengan argumen. Yang pertama adalah ekspresi dan yang kedua adalah angka, yang x pendekatan, ini dia a .

Sebagai contoh, mari kita hitung limit suatu fungsi f(x) =(x-3)/(x-1), karena x cenderung ke 1.

limit((x - 3)/(x-1),1)

MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut

ans =
   NaN

Mari kita ambil contoh lain,

limit(x^2 + 5, 3)

MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut

ans =
   14

Menghitung Batas menggunakan Oktaf

Berikut adalah versi Oktaf dari contoh di atas menggunakan simbolik paket, coba jalankan dan bandingkan hasilnya

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Oktaf akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut

ans =
   0.7142857142857142857

Verifikasi Properti Dasar Batas

Teorema Limit Aljabar memberikan beberapa sifat dasar limit. Ini adalah sebagai berikut

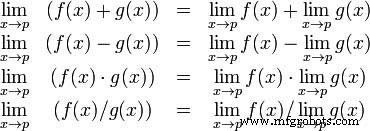
Mari kita pertimbangkan dua fungsi −

• f(x) =(3x + 5)/(x - 3)
• g(x) =x ² + 1.

Mari kita hitung limit fungsi karena x cenderung ke 5, dari kedua fungsi dan verifikasi sifat dasar limit menggunakan kedua fungsi ini dan MATLAB.

Contoh

Buat file skrip dan ketik kode berikut ke dalamnya

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Saat Anda menjalankan file, ini akan menampilkan

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Verifikasi Sifat Dasar Batas menggunakan Oktaf

Berikut adalah versi Oktaf dari contoh di atas menggunakan simbolik paket, coba jalankan dan bandingkan hasilnya

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Oktaf akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Batas Sisi Kiri dan Kanan

Ketika suatu fungsi memiliki diskontinuitas untuk beberapa nilai variabel tertentu, limitnya tidak ada pada titik itu. Dengan kata lain, limit suatu fungsi f(x) memiliki diskontinuitas di x =a, ketika nilai limit, saat x mendekati x dari sisi kiri, tidak sama dengan nilai limit saat x mendekati dari sisi kanan.

Ini mengarah pada konsep batas tangan kiri dan tangan kanan. Limit tangan kiri didefinisikan sebagai limit sebagai x -> a, dari kiri, yaitu x mendekati a, untuk nilai x a, dari kanan, yaitu x mendekati a, untuk nilai x> a. Jika limit tangan kiri dan limit tangan kanan tidak sama, maka limit tersebut tidak ada.

Mari kita pertimbangkan sebuah fungsi

f(x) =(x - 3)/|x - 3|

Kami akan menunjukkan bahwa lim_x->3 f(x) tidak ada. MATLAB membantu kita untuk menetapkan fakta ini dalam dua cara −

• Dengan memplot grafik fungsi dan menunjukkan diskontinuitasnya.
• Dengan menghitung batas dan menunjukkan bahwa keduanya berbeda.

Batas tangan kiri dan tangan kanan dihitung dengan meneruskan string karakter 'kiri' dan 'kanan' ke perintah limit sebagai argumen terakhir.

Contoh

Buat file skrip dan ketik kode berikut ke dalamnya

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Saat Anda menjalankan file, MATLAB menggambar plot berikut

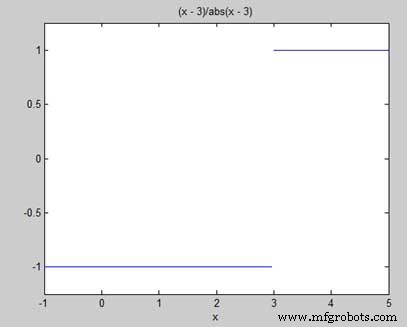
Setelah output berikut ini ditampilkan

l =
   -1
  
r =
   1