MATLAB - Diferensial

MATLAB menyediakan perbedaan perintah untuk menghitung turunan simbolik. Dalam bentuknya yang paling sederhana, Anda meneruskan fungsi yang ingin Anda bedakan ke perintah diff sebagai argumen.

Sebagai contoh, mari kita hitung turunan dari fungsi f(t) =3t ² + 2t ^-2

Contoh

Buat file skrip dan ketik kode berikut ke dalamnya

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

Ketika kode di atas dikompilasi dan dieksekusi, menghasilkan hasil sebagai berikut

ans =
6*t - 4/t^3

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

Verifikasi Aturan Dasar Diferensiasi

Mari kita nyatakan secara singkat berbagai persamaan atau aturan untuk diferensiasi fungsi dan verifikasi aturan ini. Untuk tujuan ini, kita akan menulis f'(x) untuk turunan orde pertama dan f"(x) untuk turunan orde kedua.

Berikut adalah aturan untuk diferensiasi

Aturan 1

Untuk sembarang fungsi f dan g dan sembarang bilangan real a dan b adalah turunan dari fungsi −

h(x) =af(x) + bg(x) terhadap x diberikan oleh

h'(x) =af'(x) + bg'(x)

Aturan 2

jumlah dan pengurangan Aturan menyatakan bahwa jika f dan g adalah dua fungsi, f' dan g' berturut-turut adalah turunannya, maka,

(f + g)' =f' + g'

(f - g)' =f' - g'

Aturan 3

produk Aturan menyatakan bahwa jika f dan g adalah dua fungsi, f' dan g' berturut-turut adalah turunannya, maka,

(f.g)' =f'.g + g'.f

Aturan 4

hasil bagi Aturan menyatakan bahwa jika f dan g adalah dua fungsi, f' dan g' berturut-turut adalah turunannya, maka,

(f/g)' =(f'.g - g'.f)/g ²

Aturan 5

polinomial atau aturan pangkat dasar menyatakan bahwa, jika y =f(x) =x ⁿ , maka f' =n. x ^(n-1)

Hasil langsung dari aturan ini adalah bahwa turunan dari setiap konstanta adalah nol, yaitu jika y =k , sembarang konstanta, maka

f' =0

Aturan 6

Rantai aturan menyatakan bahwa, turunan dari fungsi suatu fungsi h(x) =f(g(x)) terhadap x adalah,

h'(x)=f'(g(x)).g'(x)

Contoh

Buat file skrip dan ketik kode berikut ke dalamnya

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)

f = (x^2 + 1)^17
der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

Saat Anda menjalankan file, MATLAB menampilkan hasil berikut

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
t = sym("t");

f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 

f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 

f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 

f = (x^2 + 1)^17 
der5 = differentiate(f,x) 

f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

Turunan Fungsi Eksponensial, Logaritma, dan Trigonometri

Tabel berikut memberikan turunan dari fungsi eksponensial, logaritmik, dan trigonometri yang umum digunakan

Fungsi	Turunan
c a.x	c a.x .ln c.a (ln adalah logaritma natural)
e x	e x
ln x	1/x
lnc x	1/x.ln c
x x	x x .(1 + ln x)
sin(x)	cos(x)
cos(x)	-sin(x)
tan(x)	dtk 2 (x), atau 1/cos 2 (x), atau 1 + tan 2 (x)
dipan(x)	-csc 2 (x), atau -1/sin 2 (x), atau -(1 + cot 2 (x))
dtk(x)	dtk(x).tan(x)
csc(x)	-csc(x).cot(x)

Contoh

Buat file skrip dan ketik kode berikut ke dalamnya

syms x
y = exp(x)
diff(y)

y = x^9
diff(y)

y = sin(x)
diff(y)

y = tan(x)
diff(y)

y = cos(x)
diff(y)

y = log(x)
diff(y)

y = log10(x)
diff(y)

y = sin(x)^2
diff(y)

y = cos(3*x^2 + 2*x + 1)
diff(y)

y = exp(x)/sin(x)
diff(y)

Saat Anda menjalankan file, MATLAB menampilkan hasil berikut

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

Menghitung Derivatif Tingkat Tinggi

Untuk menghitung turunan yang lebih tinggi dari suatu fungsi f, kita menggunakan sintaks diff(f,n) .

Mari kita hitung turunan kedua dari fungsi y =f(x) =x .e ^-3x

f = x*exp(-3*x);
diff(f, 2)

MATLAB mengeksekusi kode dan mengembalikan hasil berikut

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

Contoh

Dalam contoh ini, mari kita memecahkan masalah. Diketahui suatu fungsi y =f(x) =3 sin(x) + 7 cos(5x) . Kita harus mencari tahu apakah persamaan f" + f =-5cos(2x) benar.

Buat file skrip dan ketik kode berikut ke dalamnya

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Saat Anda menjalankan file, ini akan menampilkan hasil berikut

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

Mencari Maksimal dan Minima Kurva

Jika kita mencari maxima dan minima lokal untuk sebuah graf, pada dasarnya kita mencari titik tertinggi atau terendah pada grafik fungsi di lokasi tertentu, atau untuk rentang nilai tertentu dari variabel simbolik.

Untuk fungsi y =f(x) titik-titik pada grafik yang memiliki kemiringan nol disebut titik stasioner . Dengan kata lain titik stasioner adalah dimana f'(x) =0.

Untuk menemukan titik stasioner dari suatu fungsi yang kita bedakan, kita perlu menetapkan turunannya sama dengan nol dan menyelesaikan persamaannya.

Contoh

Mari kita cari titik stasioner dari fungsi f(x) =2x ³ + 3x ² 12x + 17

Lakukan langkah-langkah berikut

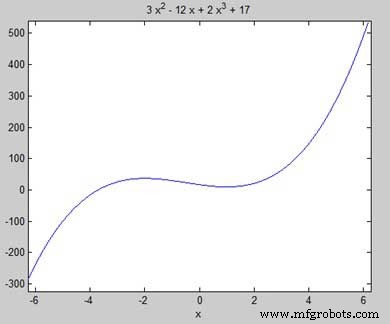
Pertama mari kita masukkan fungsi dan plot grafiknya.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

MATLAB mengeksekusi kode dan mengembalikan plot berikut

Berikut adalah kode setara Oktaf untuk contoh di atas

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

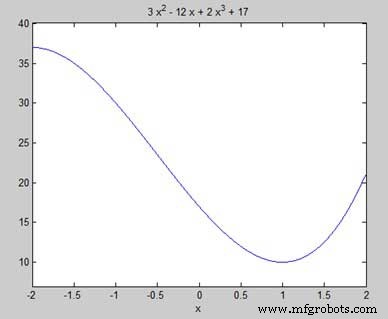
Tujuan kita adalah untuk menemukan beberapa maxima dan minima lokal pada grafik, jadi mari kita cari maxima dan minima lokal untuk interval [-2, 2] pada grafik.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

MATLAB mengeksekusi kode dan mengembalikan plot berikut

Berikut adalah kode setara Oktaf untuk contoh di atas

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Selanjutnya, mari kita hitung turunannya.

g = diff(y)

MATLAB mengeksekusi kode dan mengembalikan hasil berikut

g =
   6*x^2 + 6*x - 12

Berikut adalah Oktaf yang setara dengan perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Mari kita selesaikan fungsi turunannya, g, untuk mendapatkan nilai yang menjadi nol.

s = solve(g)

MATLAB mengeksekusi kode dan mengembalikan hasil berikut

s =
   1
   -2

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

Ini sesuai dengan plot kita. Jadi mari kita evaluasi fungsi f pada titik kritis x =1, -2. Kita dapat mengganti nilai dalam fungsi simbolik dengan menggunakan subs perintah.

subs(y, 1), subs(y, -2)

MATLAB mengeksekusi kode dan mengembalikan hasil berikut

ans =
   10
ans =
   37

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

Oleh karena itu, Nilai minimum dan maksimum pada fungsi f(x) =2x ³ + 3x ² 12x + 17, pada interval [-2,2] adalah 10 dan 37.

Menyelesaikan Persamaan Diferensial

MATLAB menyediakan dsolve perintah untuk menyelesaikan persamaan diferensial secara simbolis.

Bentuk paling dasar dari dsolve perintah untuk mencari solusi persamaan tunggal adalah

dsolve('eqn') 

dimana eqn adalah string teks yang digunakan untuk memasukkan persamaan.

Ini mengembalikan solusi simbolis dengan satu set konstanta arbitrer yang diberi label MATLAB C1, C2, dan seterusnya.

Anda juga dapat menentukan kondisi awal dan batas untuk masalah, sebagai daftar yang dibatasi koma mengikuti persamaan sebagai −

dsolve('eqn','cond1', 'cond2',…)  

Untuk tujuan penggunaan perintah dsolve, turunan dilambangkan dengan D . Misalnya, persamaan seperti f'(t) =-2*f + biaya(t) dimasukkan sebagai −

'Df =-2*f + cos(t)'

Derivatif yang lebih tinggi ditunjukkan dengan mengikuti D menurut urutan turunannya.

Misalnya persamaan f"(x) + 2f'(x) =5sin3x harus dimasukkan sebagai −

'D2y + 2Dy =5*sin(3*x)'

Mari kita ambil contoh sederhana dari persamaan diferensial orde pertama:y' =5y.

s = dsolve('Dy = 5*y')

MATLAB mengeksekusi kode dan mengembalikan hasil berikut

s =
   C2*exp(5*t)

Mari kita ambil contoh lain dari persamaan diferensial orde kedua sebagai:y" - y =0, y(0) =-1, y'(0) =2.

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB mengeksekusi kode dan mengembalikan hasil berikut

ans =
   exp(t)/2 - (3*exp(-t))/2