Apakah Transformasi Fourier itu?
Artikel ini memberi Anda informasi penting tentang teknik matematika yang memainkan peran yang sangat mendasar dalam desain sistem dan pemrosesan sinyal.
Dinamakan setelah ahli matematika Prancis Joseph Fourier, transformasi Fourier adalah prosedur matematika yang memungkinkan kita untuk menentukan konten frekuensi dari sebuah fungsi. Untuk insinyur listrik, transformasi Fourier biasanya diterapkan pada fungsi waktu yang kita sebut sinyal .
Dekomposisi Sinusoidal
Plot tegangan atau arus vs waktu, seperti yang akan kita lihat pada tampilan osiloskop, adalah representasi intuitif dari perilaku sinyal. Namun, ini bukan satu-satunya representasi yang berguna.
Dalam banyak kasus—misalnya, dalam desain sistem RF—kami terutama tertarik pada perilaku periodik sinyal. Lebih khusus, kami tertarik untuk memahami sinyal sehubungan dengan sinusoidal periodisitas, karena sinusoidal adalah ekspresi matematika unik dari frekuensi "murni".
Transformasi Fourier mengungkapkan periodisitas unsur sinyal dengan mengurai sinyal ke dalam frekuensi sinusoidal penyusunnya dan mengidentifikasi besaran dan fase dari frekuensi penyusun ini.
Kata "mengurai" sangat penting di sini. Transformasi Fourier mengajarkan kita untuk berpikir tentang sinyal domain waktu sebagai bentuk gelombang yang terdiri dari bentuk gelombang sinusoidal yang mendasarinya dengan berbagai besaran dan fase.
Gelombang persegi, misalnya, dapat didekomposisi menjadi rangkaian sinusoida tak terhingga dengan amplitudo yang terus menurun dan frekuensi yang terus meningkat. Deret yang tepat, untuk gelombang persegi berpasangan AC periode T dan amplitudo A, dapat ditulis sebagai berikut:
\[f_{persegi}(t)=\frac{4A}{\pi}\sum_{k\in{\{1,3,5,...\ }}}\frac{1}{k}\sin\left(\frac{2\pi kt}{T}\right)\]
Kita dapat mengubahnya menjadi bentuk berikut, yang sedikit lebih intuitif:
\[f_{persegi}(t)=\frac{4A}{\pi}\left(\sin(2\pi ft)+\frac{1}{3 }\sin(6\pi kaki)+\frac{1}{5}\sin(10\pi kaki)+\ ...\kanan)\]
di mana f adalah frekuensi, dalam hertz, gelombang persegi.
Plot berikut menunjukkan gelombang persegi asli, dengan warna biru, dan delapan sinusoid pertama dalam deret tak hingga.
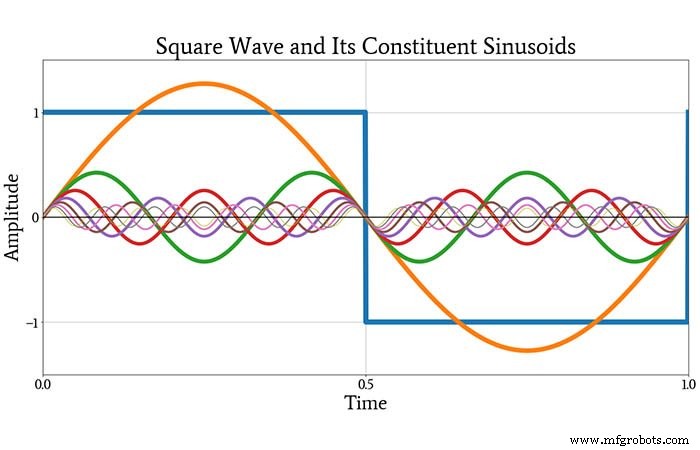
Setelah melihat plot ini, Anda mungkin masih sedikit skeptis bahwa sinusoidal ini dapat digabungkan menjadi gelombang persegi. Plot berikutnya akan meyakinkan Anda. Ini menunjukkan gelombang persegi asli dan bentuk gelombang yang dihasilkan oleh menambahkan semua sinusoid konstituen yang ditunjukkan di atas.
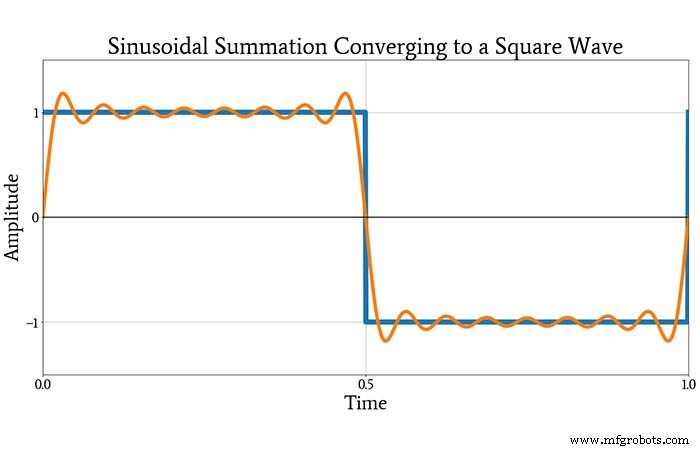
Fungsi Waktu dan Frekuensi
Ketika kita menghitung transformasi Fourier, kita mulai dengan fungsi waktu, f(t), dan melalui dekomposisi matematis, kita menghasilkan fungsi frekuensi, F(ω). (Kami biasanya menggunakan frekuensi sudut dalam diskusi teoretis tentang transformasi Fourier.)
Mengevaluasi F(ω) pada beberapa frekuensi sudut tertentu, katakanlah 100 rad/s, memberi kita besar dan fase dari komponen sinusoidal f(t) yang memiliki frekuensi 100 rad/s. Jika f(t) tidak memiliki komponen sinusoidal pada 100 rad/s, besarnya akan menjadi nol.
Anda mungkin bertanya-tanya bagaimana satu fungsi, F(ω), dapat melaporkan besaran dan fase. Transformasi Fourier menghasilkan nilai kompleks fungsi, artinya transformasi itu sendiri bukanlah besaran komponen frekuensi dalam f(t) maupun fase dari komponen-komponen tersebut. Seperti halnya bilangan kompleks, kita harus melakukan perhitungan tambahan untuk mengekstrak magnitudo atau fase.
Konsep transformasi bernilai kompleks agak lebih intuitif saat kita bekerja dengan diskrit Transformasi Fourier, bukan transformasi "standar" di mana kita mulai dengan fungsi simbolis waktu dan diakhiri dengan fungsi simbolis frekuensi.
Transformasi Fourier diskrit beroperasi pada urutan nilai numerik, dan menghasilkan urutan koefisien Fourier . Koefisien ini adalah bilangan kompleks yang khas (yaitu, mereka memiliki bentuk a + jb), dan kami biasanya menggunakan besaran bilangan kompleks ini, dihitung sebagai (a
2
+b
2
), saat menganalisis konten frekuensi sinyal.
Merencanakan Transformasi Fourier
Plot konten frekuensi sangat umum di lembar data, laporan pengujian, buku teks, dan sebagainya. Kita sering menyebut plot magnitudo vs frekuensi sebagai spektrum—misalnya, “mari kita lihat spektrum sinyal” berarti “mari kita lihat semacam representasi visual dari informasi magnitudo dalam transformasi Fourier .”
Plot berikut menunjukkan spektrum gelombang persegi berpasangan AC dengan amplitudo 1 dan frekuensi 1 Hz.
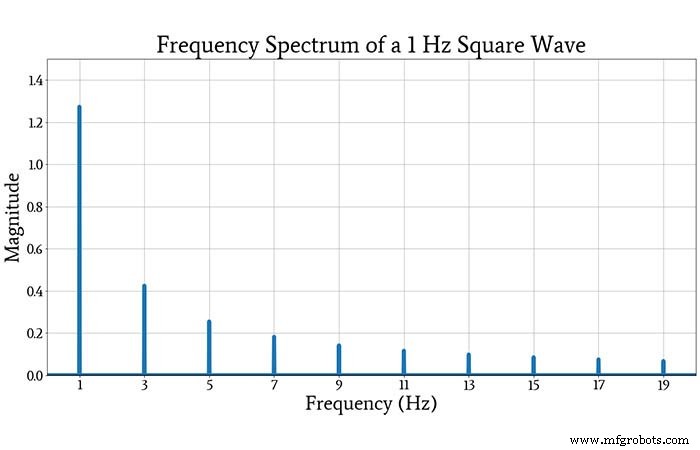
Jika Anda membandingkan amplitudo yang diplot dari "lonjakan" frekuensi dengan amplitudo komponen sinusoidal yang sesuai dalam deret tak hingga yang dibahas di atas, Anda akan melihat bahwa mereka konsisten.
Menghitung Transformasi Fourier
Kami hampir sampai di akhir artikel ini, dan saya masih belum memberi tahu Anda bagaimana kami sebenarnya menghasilkan transformasi Fourier dari sinyal yang ditentukan secara matematis.
Sejujurnya, saya tidak melihat kebutuhan untuk mengeksplorasi detail matematika secara menyeluruh dalam artikel pengantar:analisis domain frekuensi saat ini didominasi oleh teknik berbasis perangkat lunak yang ramah pengguna, dan insinyur tidak menghabiskan banyak waktu untuk mengubah waktu simbolis- ekspresi domain menjadi ekspresi domain frekuensi simbolik.
Namun demikian, dengan sesuatu yang sama pentingnya dengan transformasi Fourier, ada baiknya untuk setidaknya menyadari matematika yang mendasarinya. Jadi, tanpa basa-basi lagi, beginilah cara kita mengubah f(t) menjadi F(ω):
\[F(\omega ) =\int\limits_{ - \infty }^{ + \infty } {f(t){e^{ - j\omega t} }dt}\]
Kesimpulan
Saya harap artikel ini memberikan penjelasan yang jelas dan intuitif tentang apa itu transformasi Fourier dan bagaimana hal itu memberi kita wawasan tambahan tentang sifat sinyal.
Transformasi Fourier hanyalah awal dari rangkaian topik terkait yang luas; jika Anda ingin mempelajari lebih lanjut, lihat artikel yang tercantum di bawah ini.
Bacaan Lebih Lanjut
- Pengantar Transformasi Fourier Diskrit
- Pengantar Transformasi Fourier Cepat
- Cara Melakukan Analisis Domain-Frekuensi dengan Scilab
- Belajar Hidup di Domain Frekuensi
- Pemfilteran Linier Berdasarkan Transformasi Fourier Diskrit






