Metode Tegangan Node

Metode analisis tegangan simpul memecahkan tegangan yang tidak diketahui pada simpul rangkaian dalam hal sistem persamaan KCL. Analisis ini terlihat aneh karena melibatkan penggantian sumber tegangan dengan sumber arus yang setara. Juga, nilai resistor dalam ohm diganti dengan konduktansi ekivalen dalam siemens, G =1/R. Siemens (S) adalah satuan konduktansi, menggantikan satuan mho. Sebarang kejadian S =-1. Dan S =mho (usang).

Metode Perhitungan Tegangan Node

Kita mulai dengan rangkaian yang memiliki sumber tegangan konvensional. Node umum E₀ dipilih sebagai titik acuan. Tegangan simpul E₁ dan E₂ dihitung sehubungan dengan titik ini.

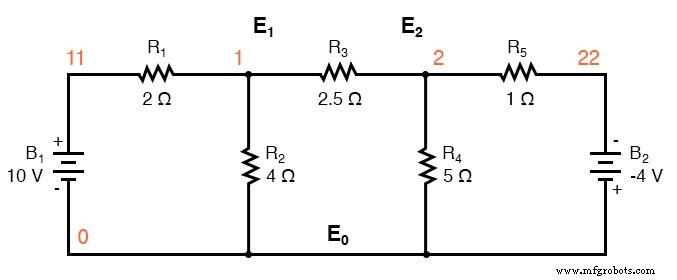
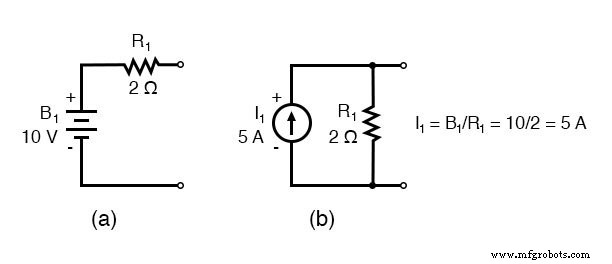
Mengganti sumber tegangan dan resistor seri terkait dengan sumber arus ekivalen dan resistor paralel menghasilkan rangkaian yang dimodifikasi. Ganti konduktansi resistor dalam siemens untuk resistansi dalam ohm.

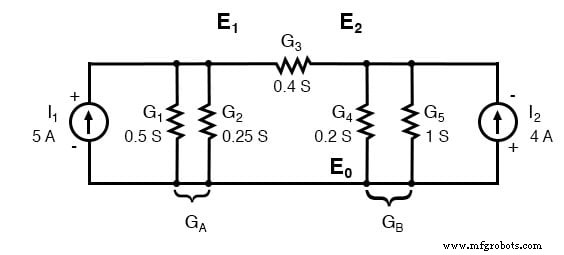
I1 =E1/R1 =10/2 =5 A I2 =E2/R5 =4/1 =4 A G1 =1/R1 =1/2 =0,5 S G2 =1/R2 =1/4 =0,25 S G3 =1/R3 =1/2,5 =0,4 S G4 =1/R4 =1/5 =0,2 S G5 =1/R5 =1/1 =1,0 S

Konduktansi paralel (resistor) dapat digabungkan dengan penambahan konduktansi. Padahal, kami tidak akan menggambar ulang sirkuit. Sirkuit siap untuk penerapan metode tegangan simpul.

GA =G1 + G2 =0,5 S + 0,25 S =0,75 S GB =G4 + G5 =0,2 S + 1 S =1,2 S

Menurunkan metode tegangan simpul umum, kami menulis sepasang persamaan KCL dalam hal tegangan simpul yang tidak diketahui V₁ dan V₂ satu kali ini. Kami melakukan ini untuk mengilustrasikan pola penulisan persamaan dengan inspeksi.

GAE1 + G3(E1 - E2) =I1 (1) GBE2 - G3(E1 - E2) =I2 (2) (GA + G3 )E1 -G3E2 =I1 (1) -G3E1 + (GB + G3)E2 =I2 (2)

Koefisien dari pasangan terakhir persamaan di atas telah disusun ulang untuk menunjukkan suatu pola. Jumlah konduktansi yang terhubung ke simpul pertama adalah koefisien positif dari tegangan pertama dalam persamaan (1). Jumlah konduktansi yang terhubung ke simpul kedua adalah koefisien positif dari tegangan kedua dalam persamaan (2). Koefisien lainnya negatif, mewakili konduktansi antara node. Untuk kedua persamaan, ruas kanan sama dengan masing-masing sumber arus yang terhubung ke simpul. Pola ini memungkinkan kita untuk dengan cepat menulis persamaan dengan inspeksi. Ini mengarah pada seperangkat aturan untuk metode analisis tegangan simpul.

Aturan Tegangan Node:

Mengubah sumber tegangan seri dengan resistor menjadi sumber arus ekuivalen dengan resistor secara paralel.
Ubah nilai resistor menjadi konduktansi.
Pilih simpul referensi(E₀ )
Tetapkan voltase yang tidak diketahui (E₁ )(E₂ ) ... (E_N )ke node yang tersisa.
Tuliskan persamaan KCL untuk setiap simpul 1,2, ... N. Koefisien positif dari tegangan pertama pada persamaan pertama adalah jumlah konduktansi yang terhubung ke simpul. Koefisien untuk tegangan kedua dalam persamaan kedua adalah jumlah konduktansi yang terhubung ke simpul itu. Ulangi untuk koefisien tegangan ketiga, persamaan ketiga, dan persamaan lainnya. Koefisien ini jatuh pada diagonal.
Semua koefisien lainnya untuk semua persamaan adalah negatif, menunjukkan konduktansi antar node. Persamaan pertama, koefisien kedua adalah konduktansi dari node 1 ke node 2, koefisien ketiga adalah konduktansi dari node 1 ke node 3. Isikan koefisien negatif untuk persamaan lainnya.
Sebelah kanan persamaan adalah sumber arus yang terhubung ke masing-masing node.
Pecahkan sistem persamaan untuk tegangan simpul yang tidak diketahui.

Contoh Metode Tegangan Node

Contoh: Siapkan persamaan dan selesaikan tegangan simpul menggunakan nilai numerik pada gambar di atas.

Solusi:

(0,5+0,25+0,4)E1 -(0,4)E2=5 -(0.4)E1 +(0.4+0.2+1.0)E2 =-4 (1.15)E1 -(0.4)E2=5 -(0.4)E1 +(1.6)E2 =-4 E1 =3,8095 E2 =-1,5476

Penyelesaian dua persamaan dapat dilakukan dengan kalkulator, atau dengan oktaf (tidak ditampilkan). Solusinya diverifikasi dengan SPICE berdasarkan diagram skema asli dengan sumber tegangan. Padahal, sirkuit dengan sumber arus dapat disimulasikan.

V1 11 0 DC 10 V2 22 0 DC -4 r1 11 1 2 r2 1 0 4 r3 1 2 2.5 r4 2 0 5 r5 2 22 1 .DC V1 10 10 1 V2 -4 -4 1 .cetak DC V(1) V(2) .akhir v(1) v(2) 3.809524e+00 -1.547619e+00

Satu lagi contoh. Yang ini memiliki tiga node. Kami tidak mencantumkan konduktansi pada diagram skematik. Namun, G₁ =1/R₁ , dll.

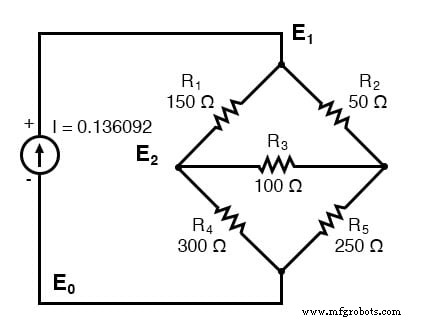
Ada tiga node untuk menulis persamaan dengan inspeksi. Perhatikan bahwa koefisien positif untuk persamaan (1) E₁ , persamaan (2) E₂ , dan persamaan (3) E₃ . Ini adalah jumlah dari semua konduktansi yang terhubung ke node. Semua koefisien lainnya negatif, mewakili konduktansi antara node. Sisi kanan persamaan adalah sumber arus terkait, 0,136092 A untuk satu-satunya sumber arus di simpul 1. Persamaan lainnya adalah nol di sisi kanan karena kekurangan sumber arus. Kami terlalu malas untuk menghitung konduktansi untuk resistor pada diagram. Jadi, G yang disubskrip adalah koefisien.

 (G1 + G2)E1 -G1E2 -G2E3 =0,136092 -G1E1 +(G1 + G3 + G4)E2 -G3E3 =0 -G2E1 -G3E2 +(G2 + G3 + G5)E3 =0

Kami sangat malas sehingga kami memasukkan resistansi timbal balik dan jumlah resistansi timbal balik ke dalam matriks oktaf "A", membiarkan oktaf menghitung matriks konduktansi setelah "A =". Baris entri awal begitu panjang sehingga dibagi menjadi tiga baris. Ini berbeda dengan contoh sebelumnya. Matriks “A” yang dimasukkan digambarkan dengan tanda kurung siku awal dan akhir. Elemen kolom dipisahkan oleh spasi. Baris adalah "baris baru" yang dipisahkan. Koma dan titik koma tidak diperlukan sebagai pemisah. Padahal, vektor arus di “b” dipisahkan dengan titik koma untuk menghasilkan vektor kolom arus.

oktaf:12> A =[1/150+1/50 -1/150 -1/50> -1/150 1/150+1/100+1/300 -1/100> -1/50 -1/100 1/50+1/100+1/250] A =0,0266667 -0,0066667 -0,02000000 -0.0066667 0.02000000 -0.0100000 -0.0200000 -0.0100000 0.0340000 oktaf:13> b =[0.136092;0;0] b =0.13609 0,00000 0,00000 oktaf:14> x=A\b x =24.000 17.655 19.310

Perhatikan bahwa koefisien diagonal matriks “A” adalah positif, Bahwa semua koefisien lainnya adalah negatif.

Solusi sebagai vektor tegangan berada di "x". E₁ =24.000 V, E₂ =17,655 V, E₃ =19,310 V. Ketiga tegangan ini dibandingkan dengan arus mesh sebelumnya dan solusi SPICE untuk masalah jembatan yang tidak seimbang. Ini bukan kebetulan, karena sumber arus 0,13609 A sengaja dipilih untuk menghasilkan 24 V yang digunakan sebagai sumber tegangan dalam masalah itu.

Ringkasan

Mengingat jaringan konduktansi dan sumber arus, metode analisis rangkaian tegangan simpul memecahkan tegangan simpul yang tidak diketahui dari persamaan KCL.
Lihat aturan di atas untuk mengetahui detail penulisan persamaan dengan inspeksi.
Satuan konduktansi G adalah siemens S. Konduktansi adalah kebalikan dari resistansi:G =1/R

LEMBAR KERJA TERKAIT:

Lembar Kerja Sirkuit Dioda Presisi
Lembar Kerja Hukum Kirchhoff

Metode dan Analisis Mesh Saat Ini Pengantar Teorema Jaringan

Teknologi Industri

Proses manufaktur

pencetakan 3D

Sistem Kontrol Otomatisasi

Teknologi Industri