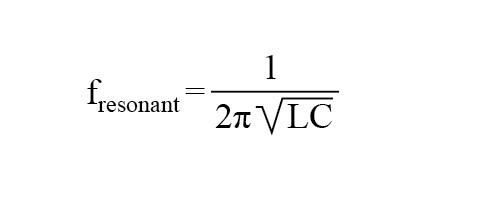Sejauh ini, desain filter yang menjadi fokus kami telah menggunakan baik kapasitor atau induktor, tetapi tidak pernah keduanya secara bersamaan. Kita harus tahu sekarang bahwa kombinasi L dan C akan cenderung beresonansi, dan properti ini dapat dimanfaatkan dalam merancang sirkuit filter band-pass dan band-stop.
Rangkaian LC seri memberikan impedansi minimum pada resonansi, sedangkan rangkaian LC paralel (“tangki”) memberikan impedansi maksimum pada frekuensi resonansinya. Mengetahui hal ini, kami memiliki dua strategi dasar untuk merancang filter band-pass atau band-stop.
Untuk filter band-pass, dua strategi resonansi dasar adalah sebagai berikut:LC seri untuk melewatkan sinyal, atau LC paralel untuk menyingkat sinyal. Kedua skema akan dikontraskan dan disimulasikan di sini:
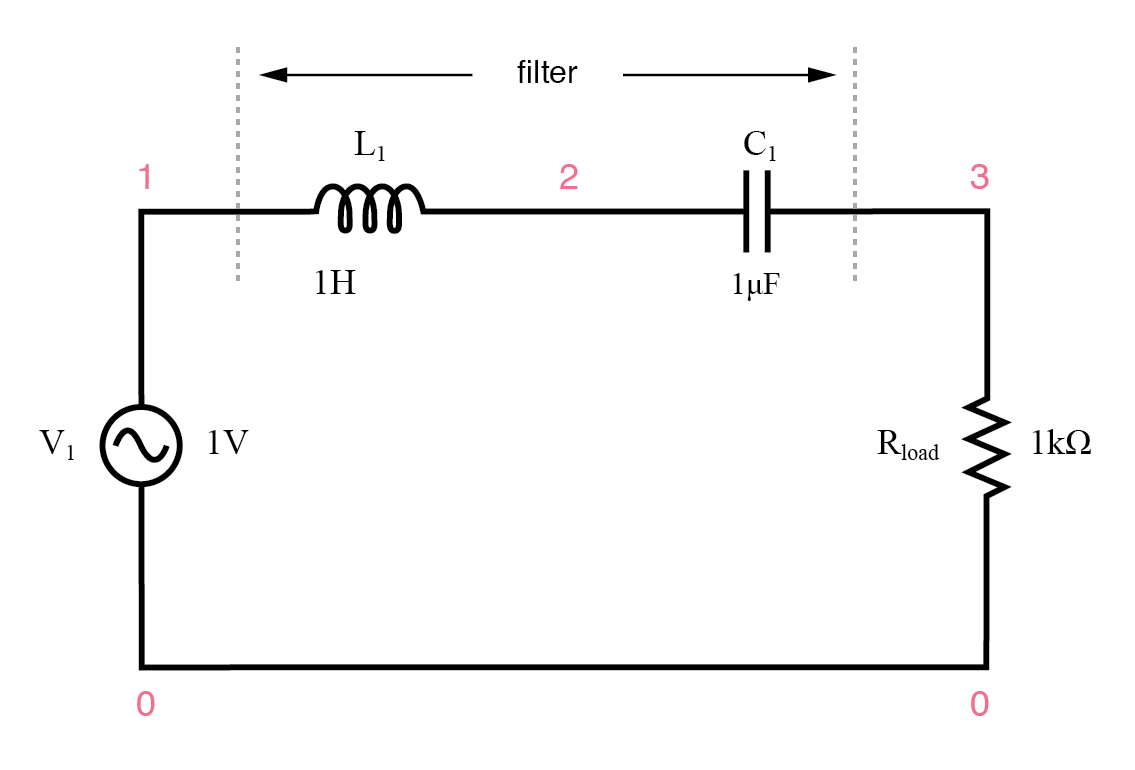
Filter band-pass LC resonansi seri.
Komponen LC seri meneruskan sinyal pada resonansi, dan memblokir sinyal frekuensi lain agar tidak sampai ke beban.
filter bandpass resonansi seri v1 1 0 ac 1 dosa l1 1 2 1 c1 2 3 1u rload 3 0 1k .ac lin 20 50 250 .plot ac v(3) .akhir
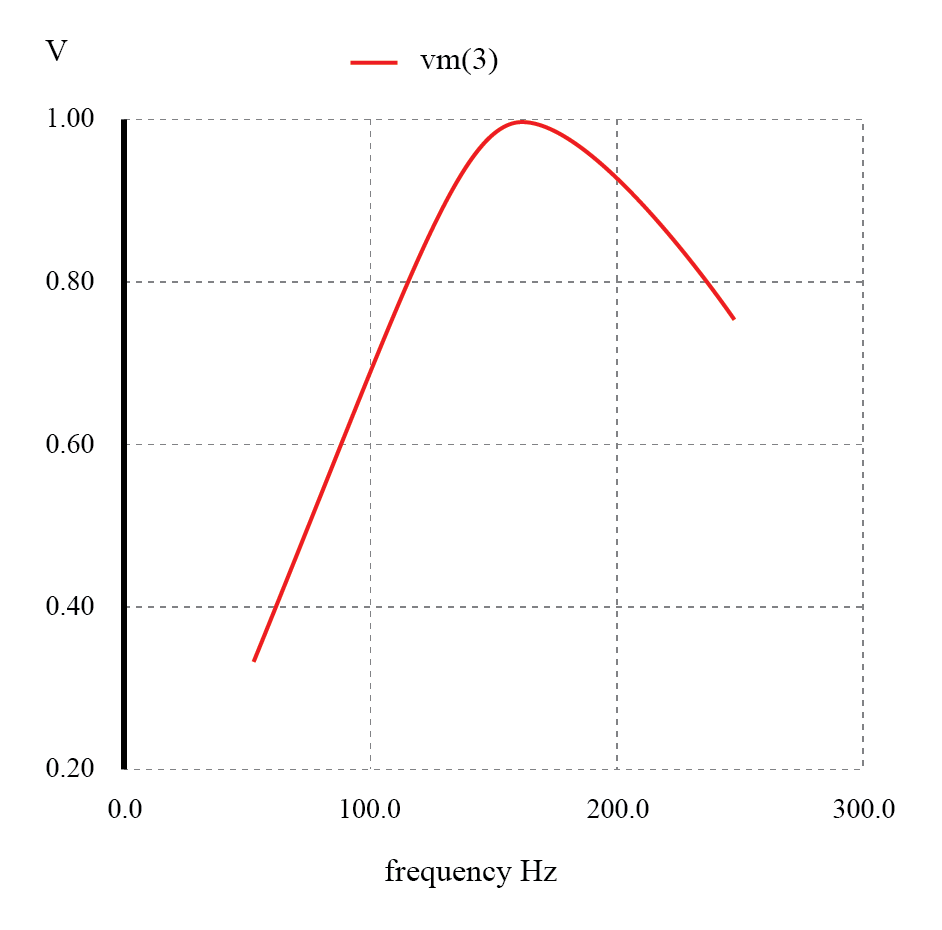
Filter band-pass resonansi seri:tegangan puncak pada frekuensi resonansi 159,15 Hz.
Beberapa hal yang perlu diperhatikan:lihat bagaimana hampir tidak ada redaman sinyal dalam “pita lulus” (rentang frekuensi di dekat puncak tegangan beban), tidak seperti filter lolos-pita yang dibuat dari kapasitor atau induktor saja.
Juga, karena filter ini bekerja berdasarkan prinsip resonansi LC seri, frekuensi resonansi yang tidak terpengaruh oleh resistansi rangkaian, nilai resistor beban tidak akan mengubah frekuensi puncak. Namun, nilai yang berbeda untuk resistor beban akan ubah "kecuraman" plot Bode ("selektivitas" filter).
Gaya dasar lain dari filter band-pass resonansi menggunakan sirkuit tangki (kombinasi LC paralel) untuk menyingkat sinyal yang terlalu tinggi atau terlalu rendah frekuensinya untuk sampai ke beban:
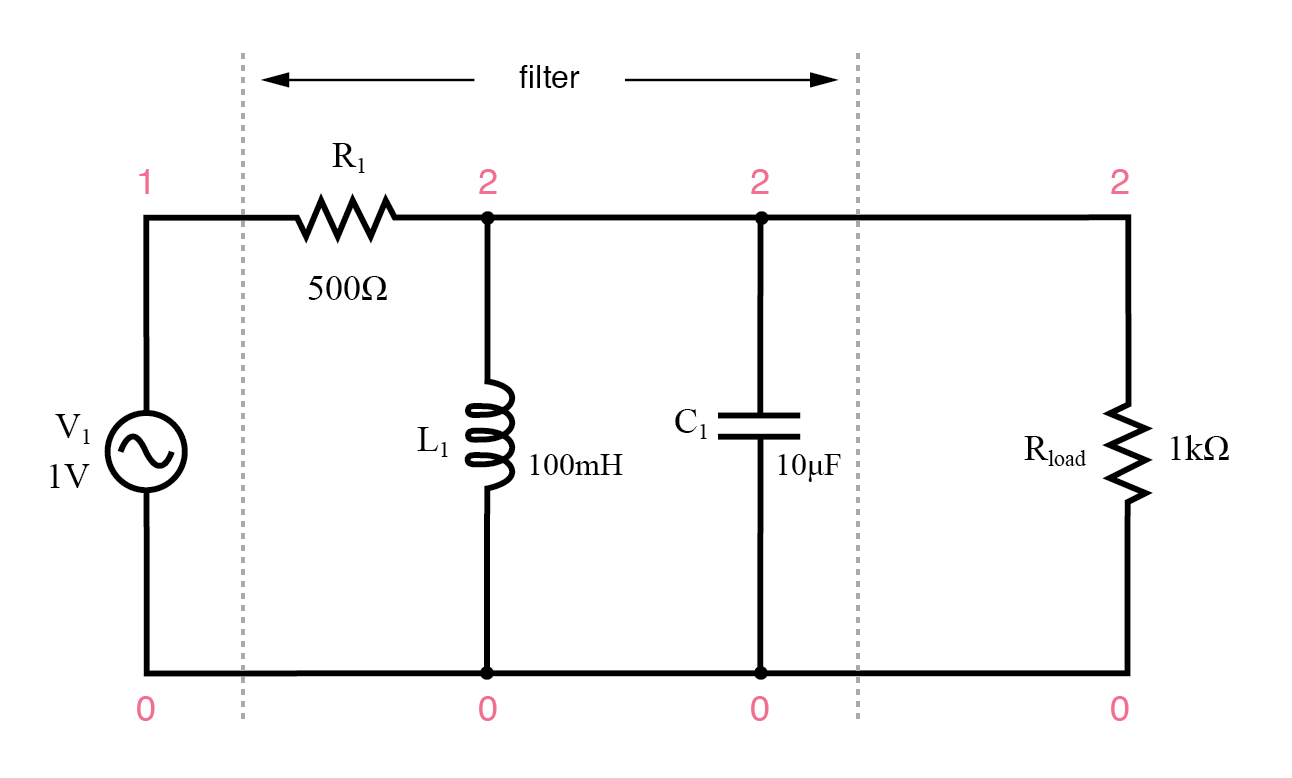
Filter band-pass resonansi paralel.
Sirkuit tangki akan memiliki banyak impedansi pada resonansi, memungkinkan sinyal untuk sampai ke beban dengan redaman minimal. Akan tetapi, di bawah atau di atas frekuensi resonansi, rangkaian tangki akan memiliki impedansi rendah, menyebabkan korsleting sinyal dan menjatuhkan sebagian besar melintasi resistor seri R1 .
filter bandpass resonansi paralel v1 1 0 ac 1 dosa r1 1 2 500 l1 2 0 100m c1 2 0 10u rload 2 0 1k .ac lin 20 50 250 .plot ac v(2) .akhir
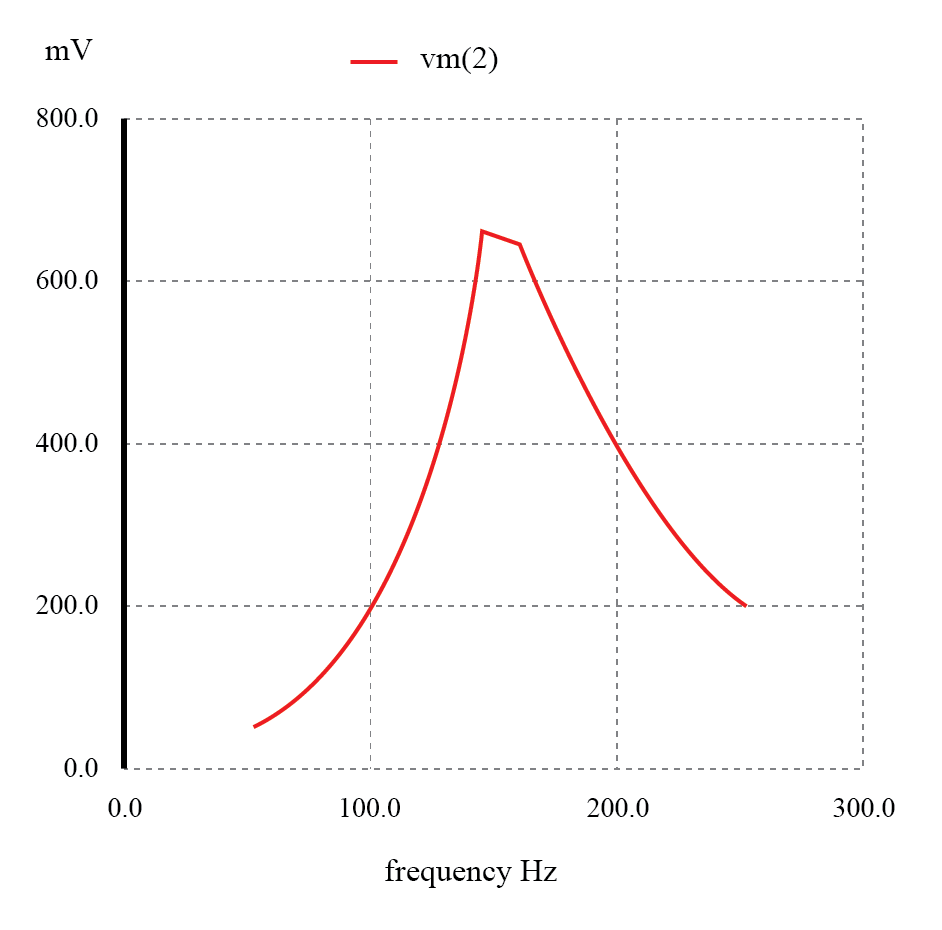
Filter resonansi paralel:tegangan memuncak pada frekuensi resonansi 159,15 Hz.
Sama seperti desain filter lolos rendah dan tinggi yang mengandalkan resistansi seri dan komponen “korsleting” paralel untuk meredam frekuensi yang tidak diinginkan, rangkaian resonansi ini tidak akan pernah dapat memberikan tegangan input (sumber) penuh ke beban.
Resistansi seri itu akan selalu menurunkan sejumlah tegangan selama ada resistansi beban yang terhubung ke output filter. Perlu dicatat bahwa bentuk rangkaian filter band-pass ini sangat populer di rangkaian penyetelan radio analog, untuk memilih frekuensi radio tertentu dari banyak frekuensi yang tersedia dari antena.
Di sebagian besar rangkaian tuner radio analog, tombol putar untuk pemilihan stasiun menggerakkan kapasitor variabel dalam rangkaian tangki.
Variabel menyetel sirkuit tangki penerima radio untuk memilih satu dari banyak stasiun siaran.
Kapasitor variabel dan induktor inti udara yang ditunjukkan pada Gambar di atas foto radio sederhana terdiri dari elemen utama dalam filter rangkaian tangki yang digunakan untuk membedakan sinyal satu stasiun radio dari yang lain.
Sama seperti kita dapat menggunakan rangkaian resonansi LC seri dan paralel untuk melewatkan hanya frekuensi-frekuensi tersebut dalam rentang tertentu, kita juga dapat menggunakannya untuk memblokir frekuensi dalam rentang tertentu, membuat filter penghenti pita. Sekali lagi, kami memiliki dua strategi utama untuk diikuti dalam melakukan ini, untuk menggunakan resonansi seri atau paralel. Pertama, kita akan melihat variasi serinya:
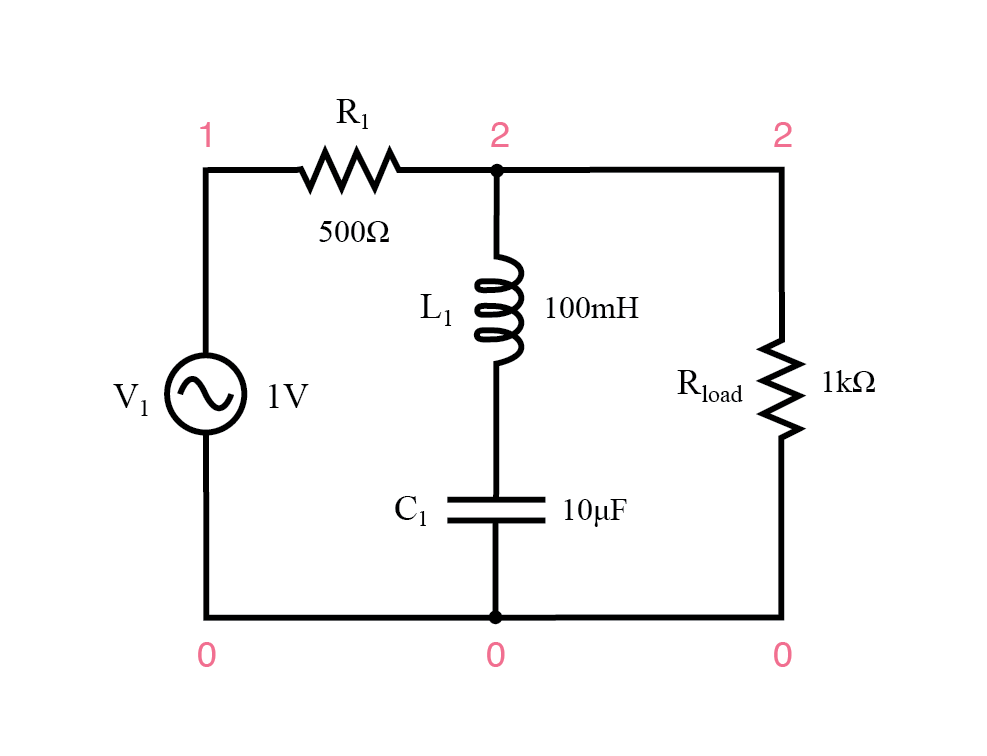
Filter penghentian pita resonansi seri.
Ketika kombinasi seri LC mencapai resonansi, impedansinya yang sangat rendah membuat sinyal menjadi pendek, menjatuhkannya ke resistor R1 dan mencegah perjalanannya ke beban.
filter bandstop resonansi seri v1 1 0 ac 1 dosa r1 1 2 500 l1 2 3 100m c1 3 0 10u rload 2 0 1k .ac lin 20 70 230 .plot ac v(2) .akhir
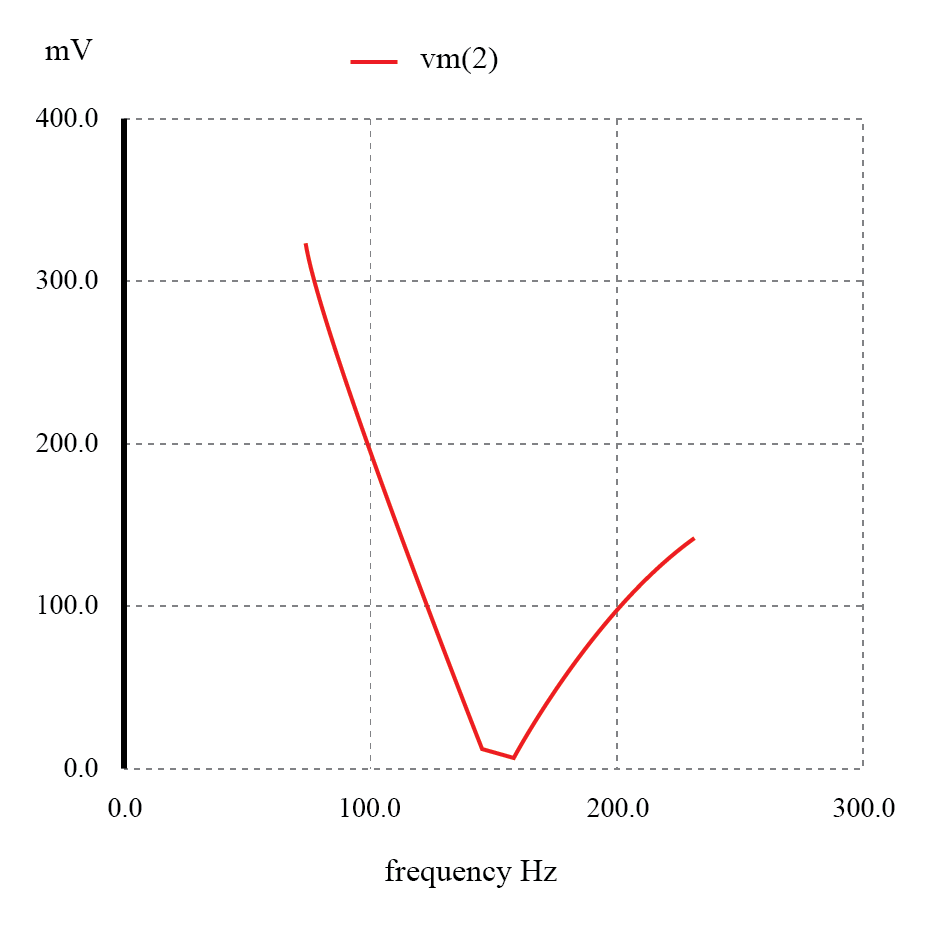
Filter penghentian pita resonansi seri:Frekuensi takik =frekuensi resonansi LC (159,15 Hz).
Selanjutnya, kita akan memeriksa filter band-stop resonansi paralel:
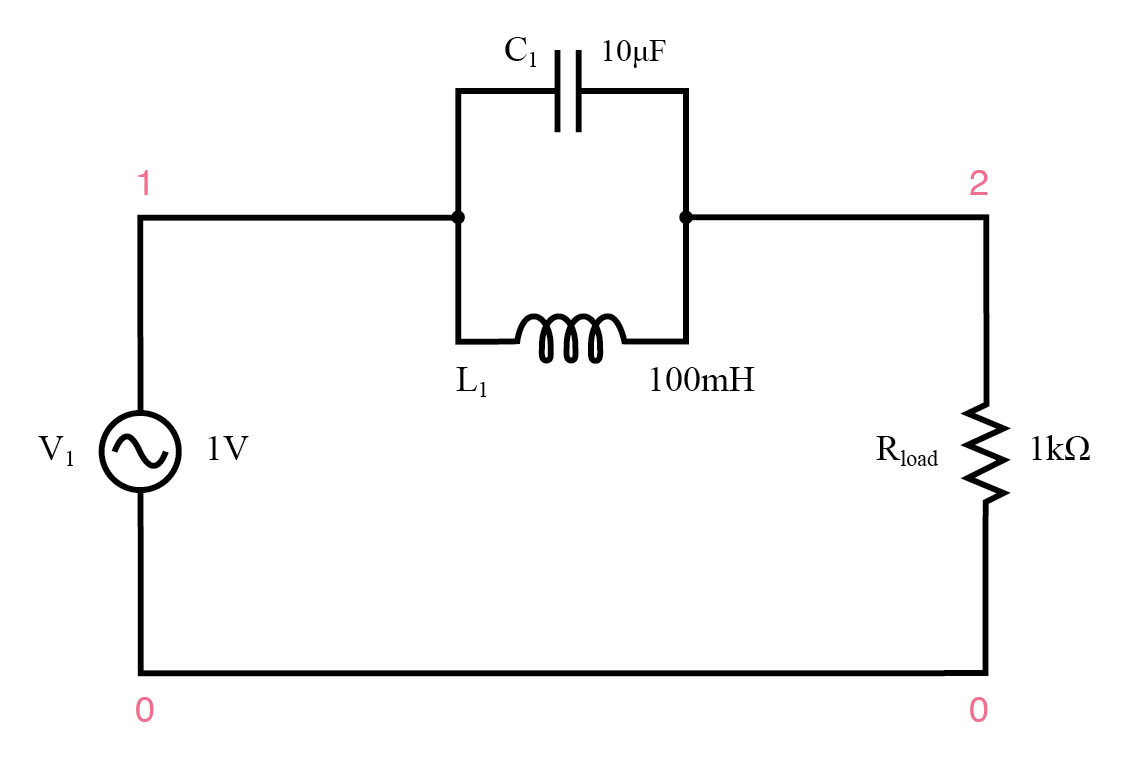
Filter penghentian pita resonansi paralel.
Komponen LC paralel menghadirkan impedansi tinggi pada frekuensi resonansi, sehingga menghalangi sinyal dari beban pada frekuensi itu. Sebaliknya, ia meneruskan sinyal ke beban pada frekuensi lain mana pun.
filter bandstop resonansi paralel v1 1 0 ac 1 dosa l1 1 2 100m c1 1 2 10u rload 2 0 1k .ac lin 20 100 200 .plot ac v(2) .akhir
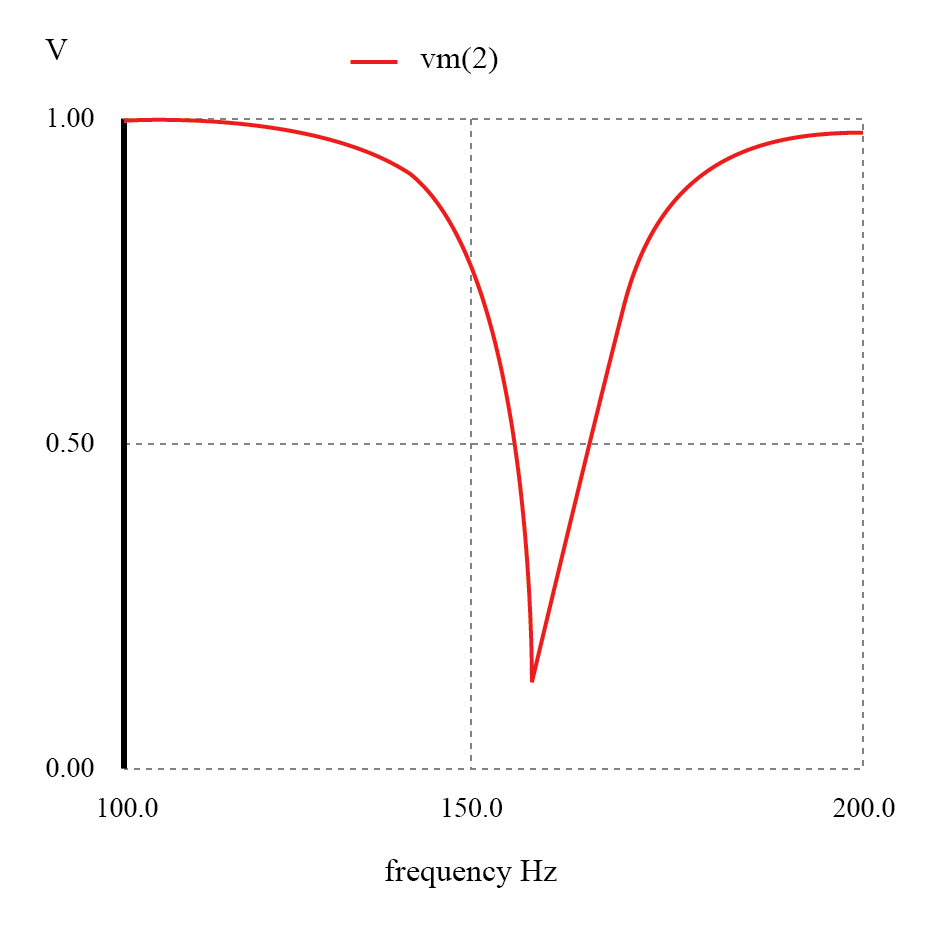
Filter penghentian pita resonansi paralel:Frekuensi takik =frekuensi resonansi LC (159,15 Hz).
Sekali lagi, perhatikan bagaimana tidak adanya resistor seri membuat redaman minimum untuk semua sinyal (lulus) yang diinginkan. Amplitudo pada frekuensi takik, di sisi lain, sangat rendah. Dengan kata lain, ini adalah filter yang sangat “selektif”.
Dalam semua desain filter resonansi ini, selektivitas sangat bergantung pada "kemurnian" induktansi dan kapasitansi yang digunakan. Jika ada hambatan yang menyimpang (terutama kemungkinan di induktor), ini akan mengurangi kemampuan filter untuk membedakan frekuensi secara halus, serta menimbulkan efek antiresonansi yang akan mengubah frekuensi puncak/takik.
Sebuah kata peringatan bagi mereka yang merancang filter lolos rendah dan lolos tinggi ada dalam urutan pada saat ini. Setelah menilai desain filter low-pass dan high-pass RC dan LR standar, mungkin terpikir oleh seorang siswa bahwa desain filter low-pass atau high-pass yang lebih baik dan lebih efektif dapat diwujudkan dengan menggabungkan elemen kapasitif dan induktif bersama-sama seperti Gambar di bawah ini.
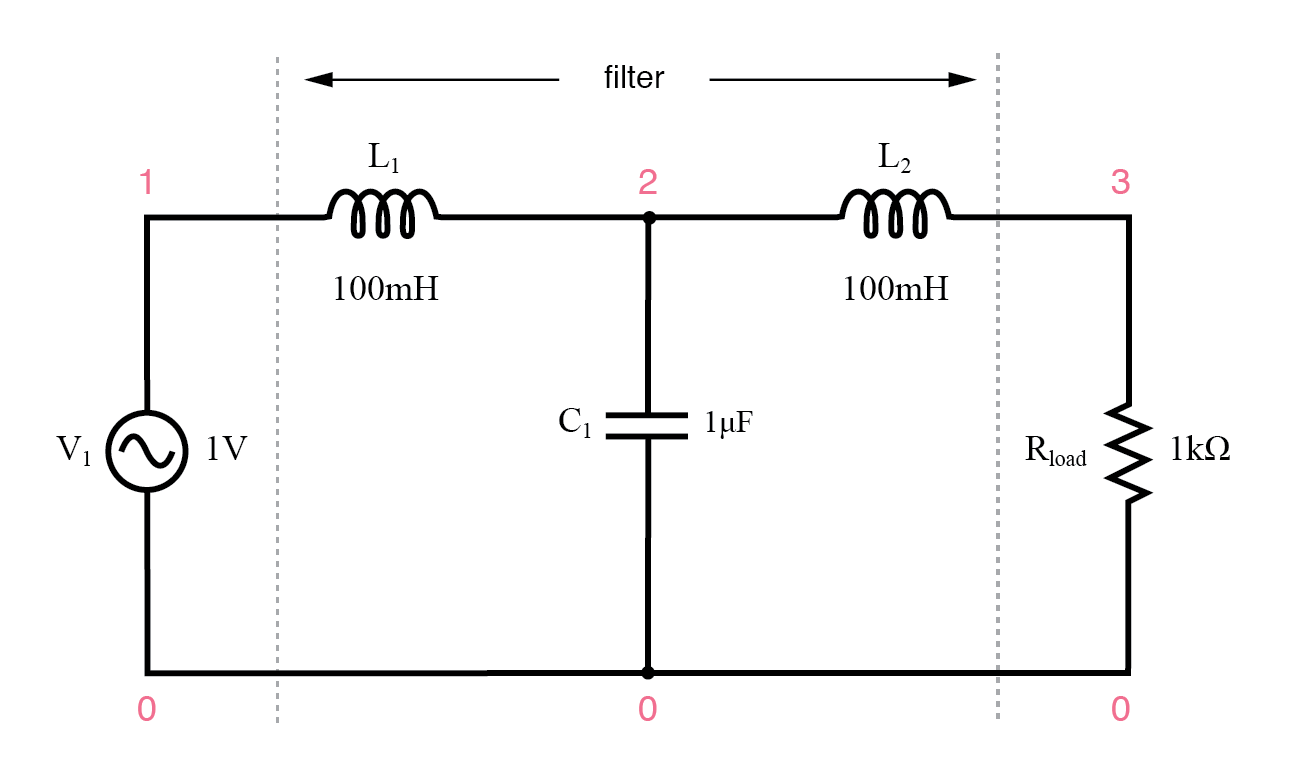
Filter low-pass induktif kapasitif.
Induktor harus memblokir frekuensi tinggi apa pun, sementara kapasitor juga harus menghubung singkat semua frekuensi tinggi, keduanya bekerja bersama untuk memungkinkan hanya sinyal frekuensi rendah yang mencapai beban.
Pada awalnya, ini tampaknya menjadi strategi yang baik, dan menghilangkan kebutuhan akan perlawanan seri. Namun, siswa yang lebih berwawasan luas akan mengenali bahwa kombinasi apa pun dari kapasitor dan induktor bersama-sama dalam suatu rangkaian kemungkinan besar akan menyebabkan efek resonansi yang terjadi pada frekuensi tertentu.
Resonansi, seperti yang telah kita lihat sebelumnya, dapat menyebabkan hal-hal aneh terjadi. Mari kita buat analisis SPICE dan lihat apa yang terjadi pada rentang frekuensi yang luas:
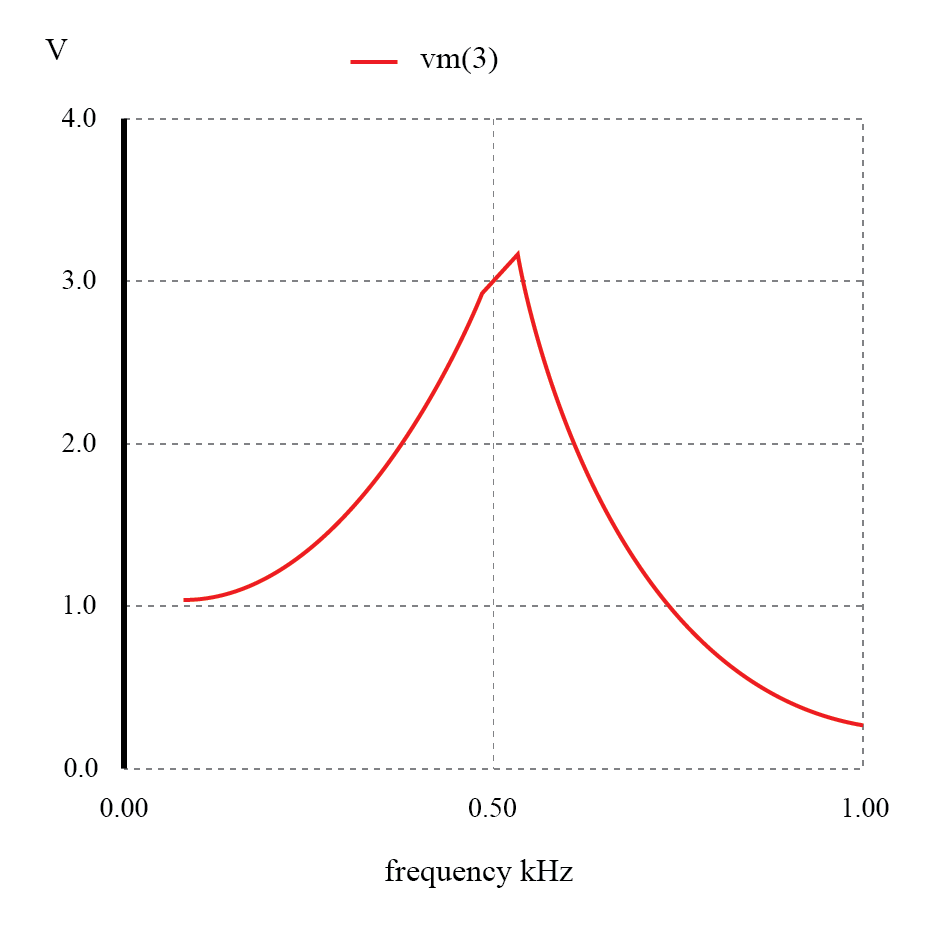
Respons tak terduga dari filter lolos rendah L-C.
Apa yang seharusnya menjadi filter low-pass ternyata menjadi filter band-pass dengan puncak sekitar 526 Hz! Kapasitansi dan induktansi dalam rangkaian filter ini mencapai resonansi pada titik tersebut, menciptakan penurunan tegangan yang besar di sekitar C1 , yang terlihat saat memuat, terlepas dari L2 pengaruh pelemahan.
Tegangan keluaran ke beban pada titik ini sebenarnya melebihi tegangan masukan (sumber)! Sedikit refleksi lagi mengungkapkan bahwa jika L1 dan C2 berada pada resonansi, mereka akan memberikan beban yang sangat berat (impedansi sangat rendah) pada sumber AC, yang mungkin juga tidak baik.
Kami akan menjalankan analisis yang sama lagi, hanya kali ini merencanakan C1 tegangan, vm(2) pada Gambar di bawah, dan arus sumber, I(v1), bersama dengan tegangan beban, vm(3):
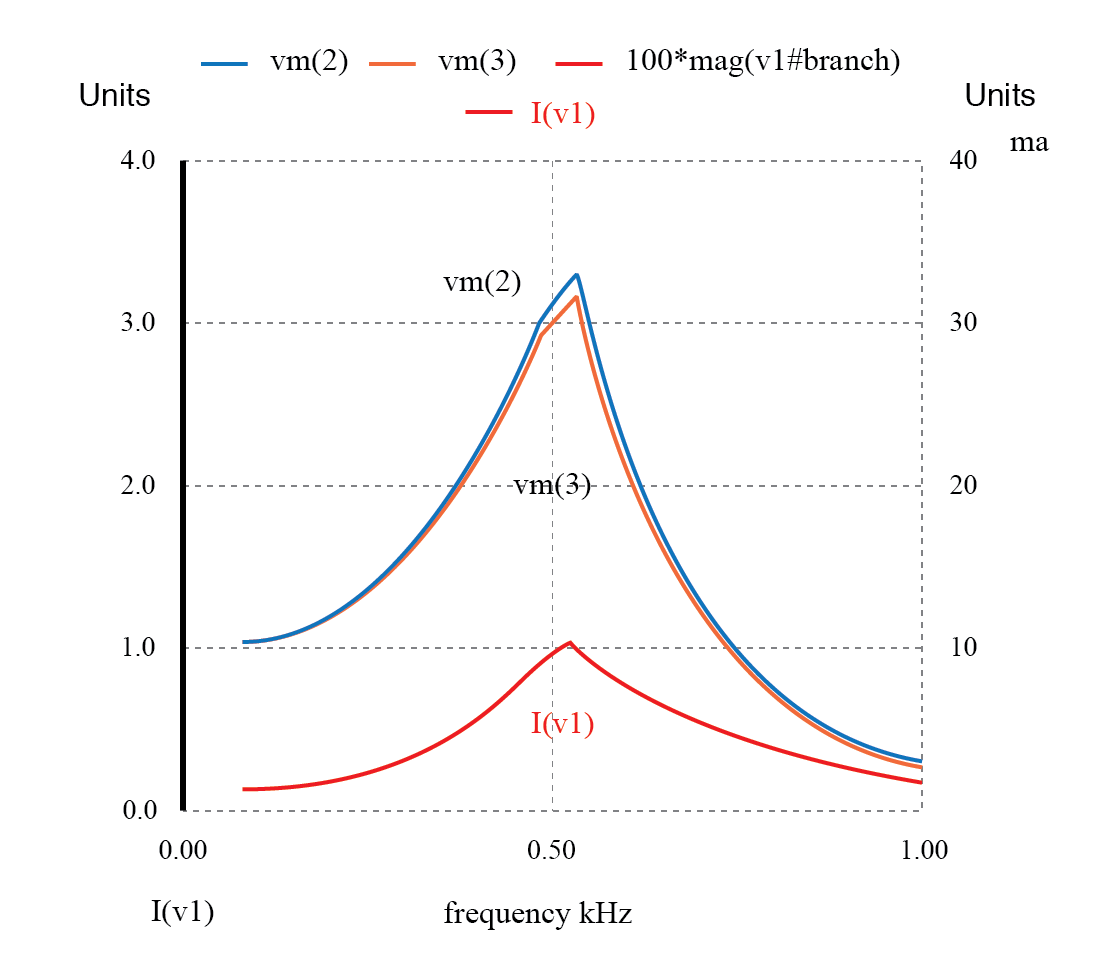
Arus meningkat pada resonansi yang tidak diinginkan dari filter lolos-rendah L-C.
Benar saja, kita melihat tegangan di C1 dan arus sumber melonjak ke titik tinggi pada frekuensi yang sama di mana tegangan beban maksimum. Jika kami mengharapkan filter ini menyediakan fungsi low-pass sederhana, kami mungkin akan kecewa dengan hasilnya.
Masalahnya adalah bahwa filter L-C memiliki impedansi input dan impedansi output yang harus dicocokkan. Impedansi sumber tegangan harus sesuai dengan impedansi input filter, dan impedansi output filter harus sesuai dengan “rbeban ” untuk tanggapan datar.
Impedansi input dan output diberikan oleh akar kuadrat dari (L/C).
Z =(L/C) 1/2
Mengambil nilai komponen dari, kita dapat menemukan impedansi filter, dan yang diperlukan , Rg dan Rmuat untuk mencocokkannya.
Untuk L=100 mH, C=1µF Z =(L/C) 1/2 =((100 mH)/(1 F)) 1/2 =316
Pada Gambar di bawah ini kami telah menambahkan Rg =316 ke generator, dan mengubah beban Rbeban dari 1000 menjadi 316 . Perhatikan bahwa jika kita perlu menggerakkan beban 1000 , rasio L/C dapat disesuaikan agar sesuai dengan hambatan tersebut.
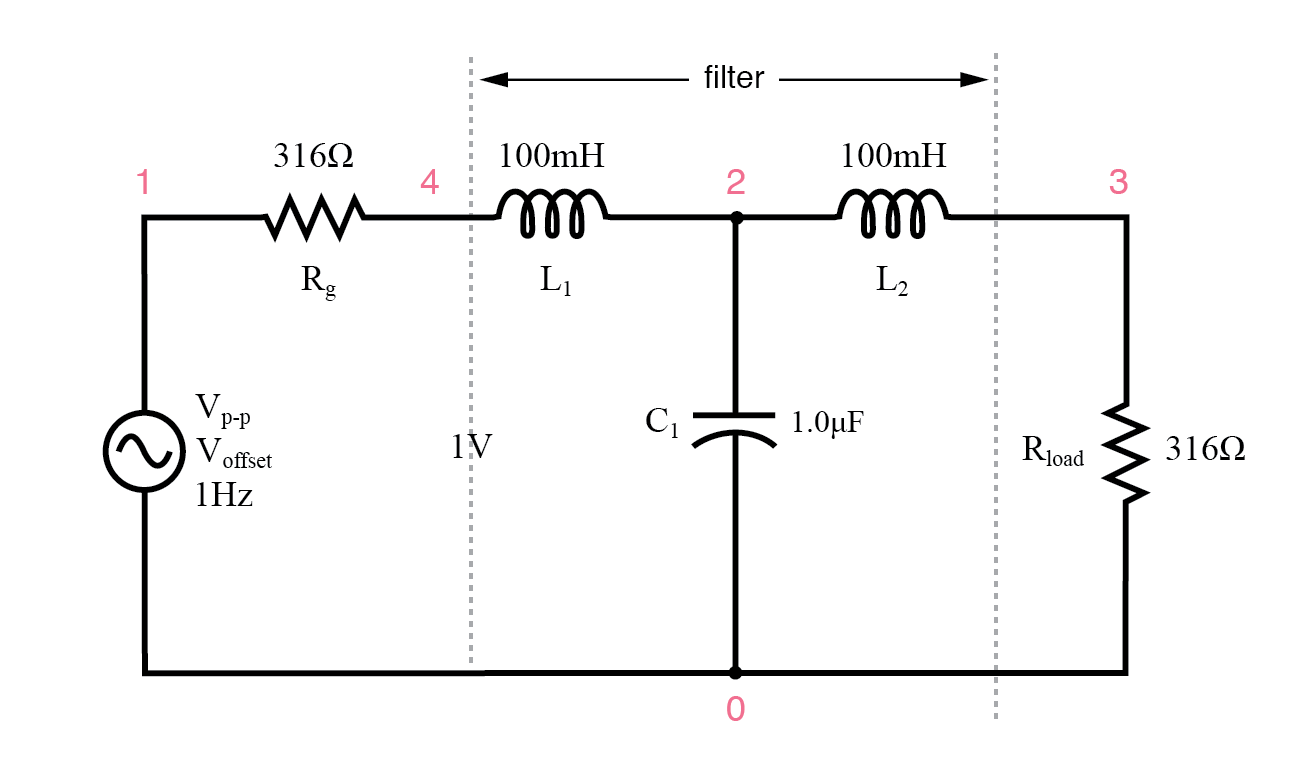
Sirkuit sumber dan filter low-pass L-C yang cocok dengan beban.
Filter lowpass yang cocok dengan LC V1 1 0 ac 1 SIN Rg 1 4 316 L1 4 2 100m C1 2 0 1.0u L2 2 3 100m Rload 3 0 316 .ac lin 20 100 1k .plot ac v(3) .akhir
Gambar di bawah menunjukkan respons “datar” dari filter lolos rendah L-C ketika impedansi sumber dan beban cocok dengan impedansi masukan dan keluaran filter.
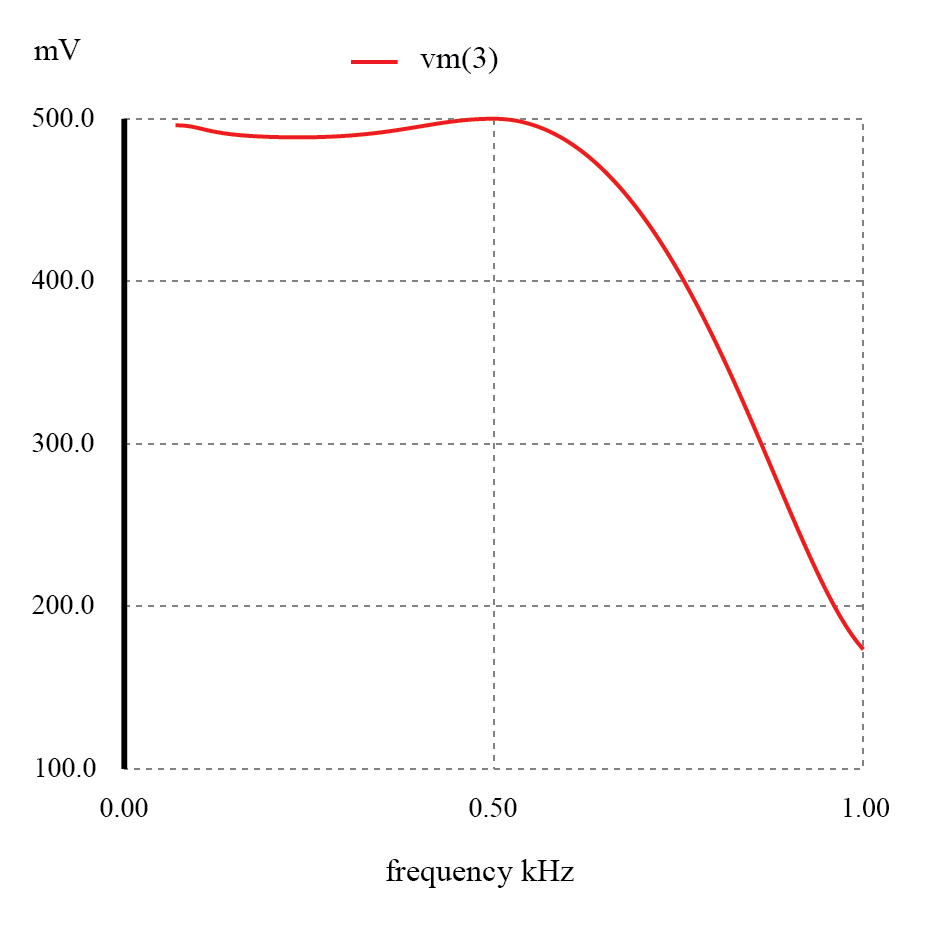
Respons dari filter low-pass L-C yang cocok dengan impedansi hampir mendatar hingga frekuensi cut-off.
Hal yang perlu diperhatikan dalam membandingkan respons filter yang tidak cocok dengan filter yang cocok adalah bahwa beban variabel pada filter menghasilkan perubahan tegangan yang cukup besar. Properti ini secara langsung berlaku untuk catu daya yang difilter L-C– regulasi miskin. Tegangan catu daya berubah dengan perubahan beban. Ini tidak diinginkan.
Pengaturan beban yang buruk ini dapat dikurangi dengan swinging choke . Ini adalah tersedak , induktor, dirancang untuk menjenuhkan ketika arus DC yang besar melewatinya.
Dengan jenuh, yang kami maksud adalah bahwa arus DC menciptakan tingkat fluks yang "terlalu" di inti magnet, sehingga komponen arus AC tidak dapat memvariasikan fluks. Karena induksi sebanding dengan dΦ/dt, induktansi berkurang oleh arus DC yang besar.
Penurunan induktansi menurunkan reaktansi XL . Menurunkan reaktansi, mengurangi jatuh tegangan pada induktor; dengan demikian, meningkatkan tegangan pada output filter. Hal ini meningkatkan regulasi tegangan sehubungan dengan beban variabel.
Terlepas dari resonansi yang tidak diinginkan, filter low-pass yang terdiri dari kapasitor dan induktor sering digunakan sebagai tahap akhir dalam catu daya AC/DC untuk menyaring tegangan “riak” AC yang tidak diinginkan dari DC yang dikonversi dari AC.
Mengapa demikian, jika desain filter khusus ini memiliki titik resonansi yang berpotensi merepotkan?
Jawabannya terletak pada pemilihan ukuran komponen filter dan frekuensi yang ditemui dari konverter AC/DC (rectifier). Apa yang kami coba lakukan dalam filter catu daya AC/DC adalah memisahkan tegangan DC dari sejumlah kecil tegangan AC frekuensi relatif tinggi.
Induktor dan kapasitor filter umumnya cukup besar (biasanya beberapa Henry untuk induktor dan ribuan F untuk kapasitor), membuat frekuensi resonansi filter sangat, sangat rendah. DC tentu saja memiliki “frekuensi” nol, jadi tidak mungkin sirkuit LC dapat beresonansi.
Tegangan riak, di sisi lain, adalah tegangan AC non-sinusoidal yang terdiri dari frekuensi dasar setidaknya dua kali frekuensi tegangan AC yang dikonversi, dengan harmonik berkali-kali lipat.
Untuk catu daya plug-in-the-wall yang berjalan pada daya 60 Hz AC (60 Hz Amerika Serikat; 50 Hz di Eropa), frekuensi terendah yang pernah dilihat filter adalah 120 Hz (100 Hz di Eropa), yang jauh di atas titik resonansinya. Oleh karena itu, titik resonansi yang berpotensi menyusahkan dalam filter semacam itu benar-benar dihindari.
Analisis SPICE berikut menghitung output tegangan (AC dan DC) untuk filter tersebut, dengan sumber tegangan seri DC dan AC (120 Hz) memberikan perkiraan kasar dari output frekuensi campuran dari konverter AC/DC.
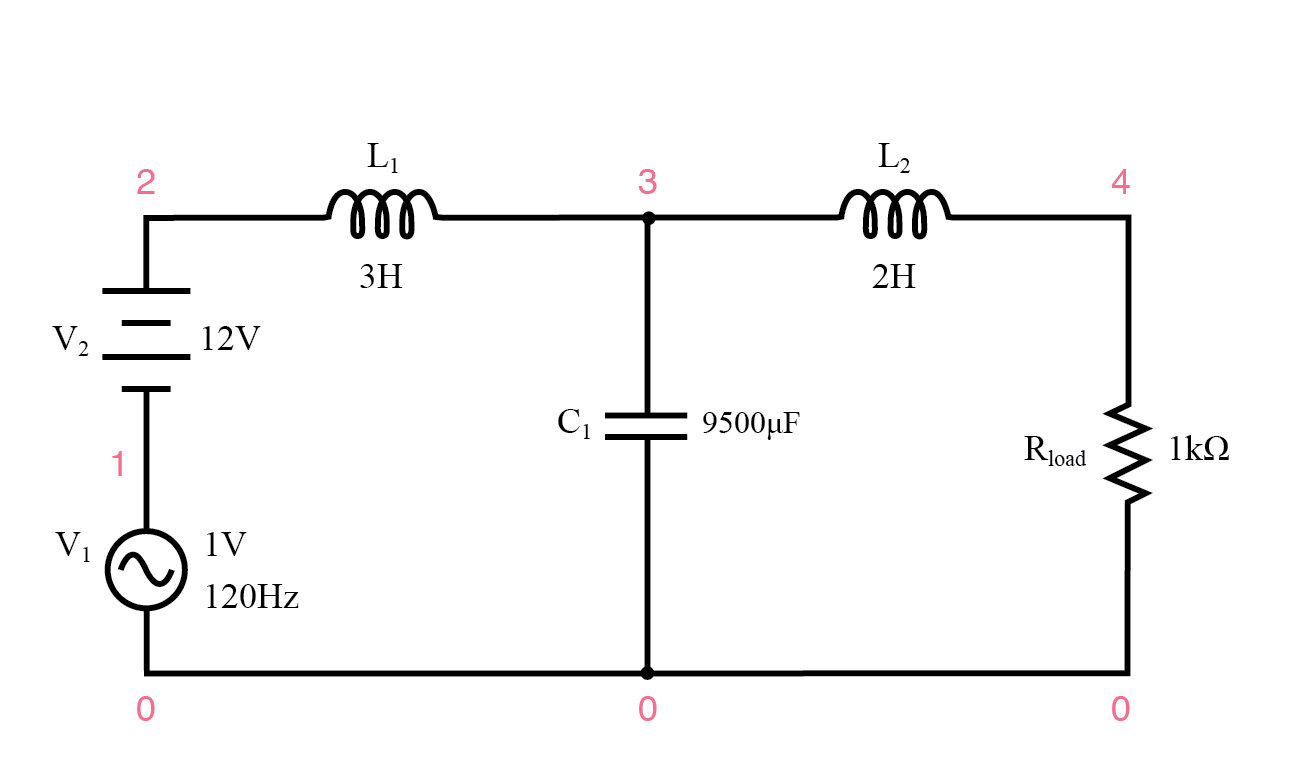
Filter catu daya AC/DC memberikan daya DC "bebas riak".
Filter catu daya AC/DC memberikan daya DC "bebas riak" filter catu daya ac/dc v1 1 0 ac 1 dosa v2 2 1 dc l1 2 3 3 c1 3 0 9500u l2 3 4 2 rload 4 0 1k .dc v2 12 12 1 .ac lin 1 120 120 .cetak dc v(4) .cetak ac v(4) .akhir v2 v(4) 1.200E+01 1.200E+01 Tegangan DC pada beban =12 volt frekuensi v(4) 1.200E+02 3.412E-05 Tegangan AC pada beban =34.12 mikrovolt
Dengan tegangan DC 12 volt penuh pada beban dan hanya tersisa 34,12 V AC dari sumber AC 1 volt yang dikenakan di seluruh beban, desain rangkaian ini membuktikan dirinya sebagai filter catu daya yang sangat efektif.
Pelajaran yang dipelajari di sini tentang efek resonansi juga berlaku untuk desain filter lolos tinggi menggunakan kapasitor dan induktor. Selama frekuensi yang diinginkan dan tidak diinginkan berada di kedua sisi titik resonansi, filter akan bekerja dengan baik.
Tetapi jika ada sinyal dengan magnitudo signifikan yang mendekati frekuensi resonansi diterapkan pada input filter, hal-hal aneh akan terjadi!
TINJAUAN:
LEMBAR KERJA TERKAIT:
Teknologi Industri
Umumnya, filter adalah proses atau perangkat yang menghilangkan fitur/komponen yang tidak perlu dari sinyal frekuensi selama pemrosesan sinyal. Mereka umum dalam grafik komputer, pemrosesan gambar, sistem kontrol, radar, telekomunikasi, dll. Terlebih lagi, ada berbagai jenis filter yang akan kita pe
Para ahli sepakat bahwa penyebab nomor satu kegagalan sistem hidraulik adalah kontaminasi. Filter hidraulik membantu menjebak kontaminasi sebelum dapat menuju ke hilir dalam sistem, tetapi filter yang diabaikan bisa lebih buruk daripada tidak memiliki filter sama sekali. Filter yang tersumbat tidak
Filtrasi vakum adalah metode pemisahan yang digunakan untuk menghilangkan padatan dari cairan. Umumnya padatan dilarutkan dalam larutan. Solusinya bisa tak jenuh, jenuh, atau lewat jenuh — perbedaannya adalah konsentrasi padatan dalam cairan. Filter digunakan untuk memisahkan padatan dari cairan, da
Bilik semprot adalah lingkungan tertutup yang dibangun untuk tujuan khusus mengaplikasikan cat semprot, biasanya untuk kendaraan bermotor. Bilik semprotan disegel untuk mencegah debu dan partikel lain mencemari udara di dalamnya. Partikel-partikel ini akan mempengaruhi hasil akhir cat. Udara bersih
