Pengukuran Frekuensi dan Fase

Besaran listrik penting yang tidak setara dalam rangkaian DC adalah frekuensi .

Pengukuran frekuensi sangat penting dalam banyak aplikasi arus bolak-balik, terutama pada sistem daya AC yang dirancang untuk bekerja secara efisien pada satu frekuensi dan satu frekuensi saja.

Jika AC dihasilkan oleh alternator elektromekanis, frekuensi akan berbanding lurus dengan kecepatan poros mesin, dan frekuensi dapat diukur hanya dengan mengukur kecepatan poros.

Namun, jika frekuensi perlu diukur pada jarak tertentu dari alternator, cara pengukuran lain akan diperlukan.

Metode Pengukuran Frekuensi

Menggunakan Prinsip Resonansi Mekanik

Salah satu metode pengukuran frekuensi yang sederhana namun kasar dalam sistem tenaga menggunakan prinsip resonansi mekanis. Setiap objek fisik yang memiliki sifat elastisitas (kekenyalan) memiliki frekuensi inheren di mana ia akan lebih suka bergetar.

Garpu tala adalah contoh yang bagus untuk hal ini:pukul satu kali dan garpu tala akan terus bergetar dengan nada yang sesuai dengan panjangnya. Garpu tala yang lebih panjang memiliki frekuensi resonansi yang lebih rendah:nadanya akan lebih rendah pada skala musik daripada garpu tala yang lebih pendek.

Bayangkan deretan garpu tala berukuran progresif yang disusun berdampingan. Semuanya dipasang pada alas yang sama, dan alas tersebut digetarkan pada frekuensi tegangan (atau arus) AC yang diukur melalui elektromagnet.

Garpu tala mana yang paling dekat frekuensi resonansinya dengan frekuensi getaran itu akan cenderung bergetar paling besar (atau paling keras). Jika garpunya cukup tipis, kita bisa melihat gerakan relatif masing-masing dengan panjang keburaman yang akan kita lihat saat kita memeriksa masing-masing dari perspektif tampilan akhir.

Nah, buat koleksi "garpu tala" dari potongan lembaran logam yang dipotong dengan pola yang mirip dengan penggaruk, dan Anda memiliki buluh bergetar pengukur frekuensi:

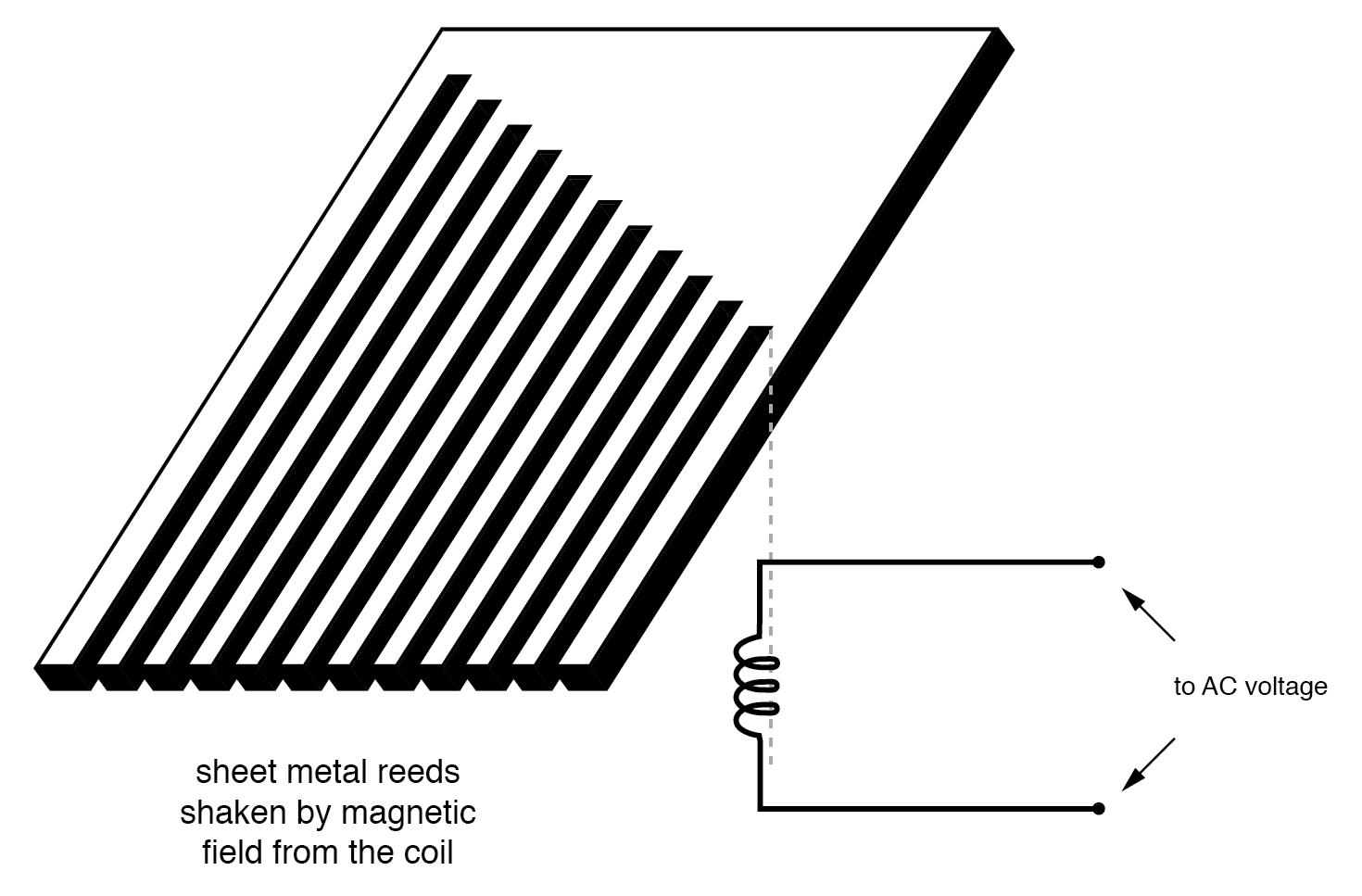
Diagram pengukur frekuensi buluh bergetar.

Pengguna meteran ini melihat ujung semua buluh yang tidak sama panjangnya saat mereka secara kolektif diguncang pada frekuensi tegangan AC yang diberikan ke koil. Yang paling dekat frekuensi resonansinya dengan AC yang digunakan akan paling bergetar, terlihat seperti:

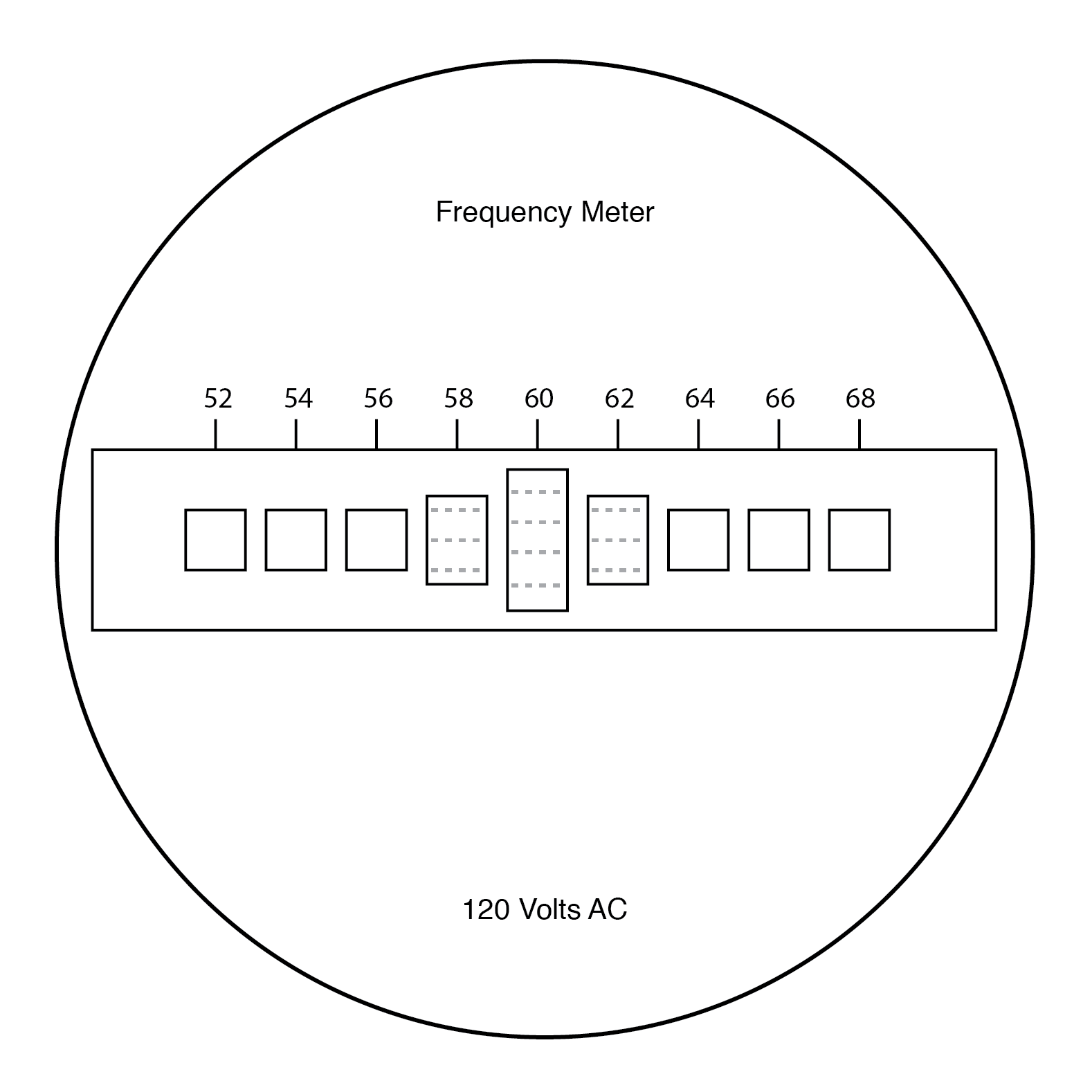
Panel depan pengukur frekuensi buluh bergetar.

Pengukur buluh getar, tentu saja, bukanlah instrumen presisi, tetapi sangat sederhana dan oleh karena itu mudah dibuat agar kokoh. Mereka sering ditemukan pada genset kecil yang digerakkan mesin untuk tujuan mengatur kecepatan mesin sehingga frekuensinya mendekati 60 (50 di Eropa) Hertz.

Menggunakan bentuk Tangki Sirkuit

Sementara meter jenis buluh tidak tepat, prinsip operasionalnya tidak. Sebagai pengganti resonansi mekanis, kita dapat mengganti resonansi listrik dan merancang pengukur frekuensi menggunakan induktor dan kapasitor dalam bentuk rangkaian tangki (induktor paralel dan kapasitor). Lihat Gambar di bawah.

Satu atau kedua komponen dibuat dapat disesuaikan, dan meteran ditempatkan di sirkuit untuk menunjukkan amplitudo maksimum tegangan di kedua komponen.

Kenop penyesuaian dikalibrasi untuk menunjukkan frekuensi resonansi untuk pengaturan tertentu, dan frekuensi dibaca darinya setelah perangkat disetel untuk indikasi maksimum pada meteran.

Pada dasarnya, ini adalah rangkaian filter yang dapat disetel yang disesuaikan dan kemudian dibaca dengan cara yang mirip dengan rangkaian jembatan (yang harus diseimbangkan untuk kondisi "null" dan kemudian dibaca).

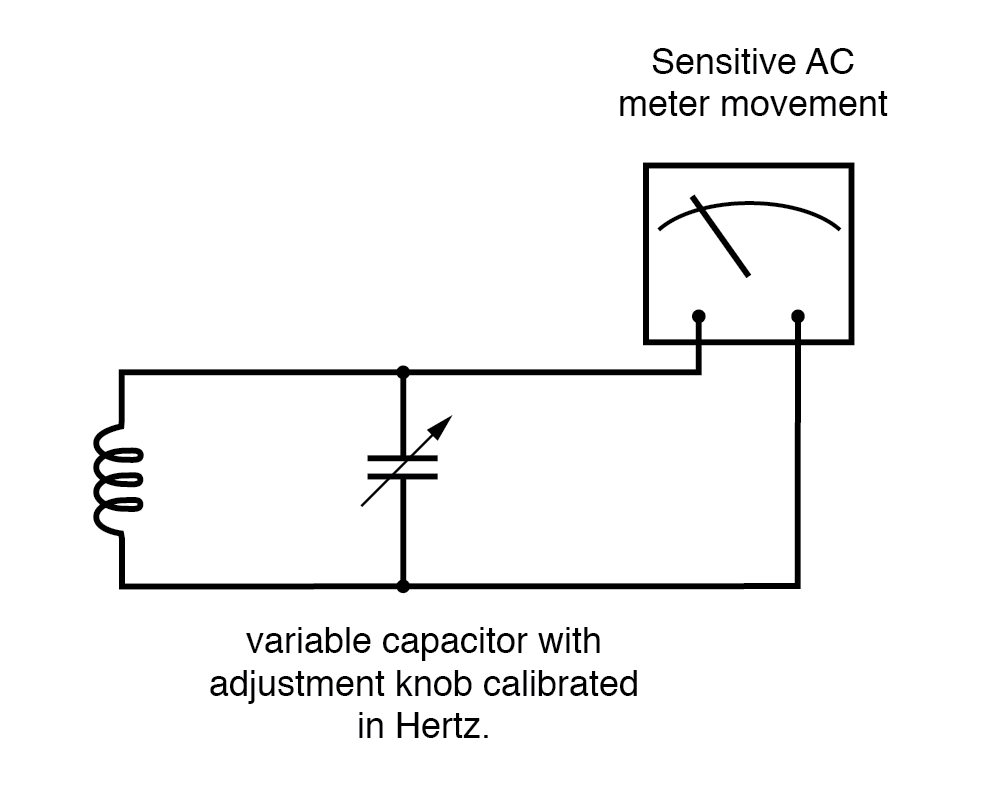
Pengukur frekuensi resonansi "memuncak" saat frekuensi resonansi L-C disetel untuk menguji frekuensi.

Teknik ini populer untuk operator radio amatir (atau setidaknya sebelum munculnya instrumen frekuensi digital murah yang disebut penghitung ), terutama karena tidak memerlukan koneksi langsung ke sirkuit.

Selama induktor dan/atau kapasitor dapat mencegat cukup medan nyasar (magnetik atau listrik, masing-masing) dari rangkaian yang diuji untuk menyebabkan meteran menunjukkan, itu akan berfungsi.

Dalam frekuensi seperti pada jenis pengukuran listrik lainnya, cara pengukuran yang paling akurat biasanya adalah pengukuran di mana kuantitas yang tidak diketahui dibandingkan dengan standar yang diketahui. , instrumen dasar tidak melakukan apa-apa selain menunjukkan ketika dua kuantitas sama satu sama lain.

Ini adalah prinsip dasar di balik rangkaian jembatan DC (Wheatstone) dan merupakan prinsip metrologi suara yang diterapkan di seluruh sains. Jika kita memiliki akses ke standar frekuensi yang akurat (sumber tegangan AC yang memegang sangat tepat pada frekuensi tunggal), pengukuran frekuensi yang tidak diketahui, sebagai perbandingan, seharusnya relatif mudah.

Menggunakan Kristal Kuarsa

Untuk standar frekuensi tersebut, kita kembalikan perhatian kita pada garpu tala, atau setidaknya variasi yang lebih modern yang disebut kristal kuarsa .

Kuarsa adalah mineral alami yang memiliki sifat yang sangat menarik yang disebut piezoelektrik . Bahan piezoelektrik menghasilkan tegangan sepanjang panjangnya saat ditekan secara fisik, dan akan berubah bentuk secara fisik ketika tegangan eksternal diterapkan pada panjangnya.

Deformasi ini sangat, sangat sedikit dalam banyak kasus, tetapi memang ada.

Batu kuarsa bersifat elastis (kenyal) dalam rentang kecil pembengkokan yang akan dihasilkan oleh tegangan eksternal, yang berarti bahwa ia akan memiliki frekuensi resonansi mekanisnya sendiri yang mampu dimanifestasikan sebagai sinyal tegangan listrik.

Dengan kata lain, jika sebuah chip kuarsa dipukul, ia akan "berdering" dengan frekuensi uniknya sendiri yang ditentukan oleh panjang chip, dan osilasi resonansi itu akan menghasilkan tegangan yang setara di beberapa titik chip kuarsa yang dapat disadap. ke dalam dengan kabel yang dipasang pada permukaan chip.

Secara timbal balik, chip kuarsa akan cenderung paling bergetar saat “dirangsang” oleh tegangan AC yang diterapkan pada frekuensi yang tepat, seperti buluh pada pengukur frekuensi buluh getar.

Serpihan batu kuarsa dapat dipotong dengan tepat untuk frekuensi resonansi yang diinginkan, dan keping itu dipasang dengan aman di dalam cangkang pelindung dengan kabel yang diperpanjang untuk koneksi ke sirkuit listrik eksternal.

Saat dikemas seperti itu, perangkat yang dihasilkan hanya disebut kristal (atau terkadang “xtal ”). Simbol skema ditunjukkan pada gambar di bawah ini.

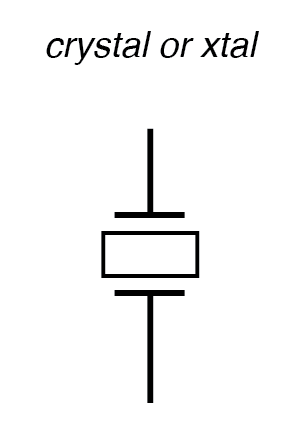
Simbol skema kristal (elemen penentu frekuensi).

Secara elektrik, chip kuarsa itu setara dengan rangkaian resonansi LC seri. (Gambar di bawah) Sifat dielektrik kuarsa menyumbang elemen kapasitif tambahan ke rangkaian ekivalen.

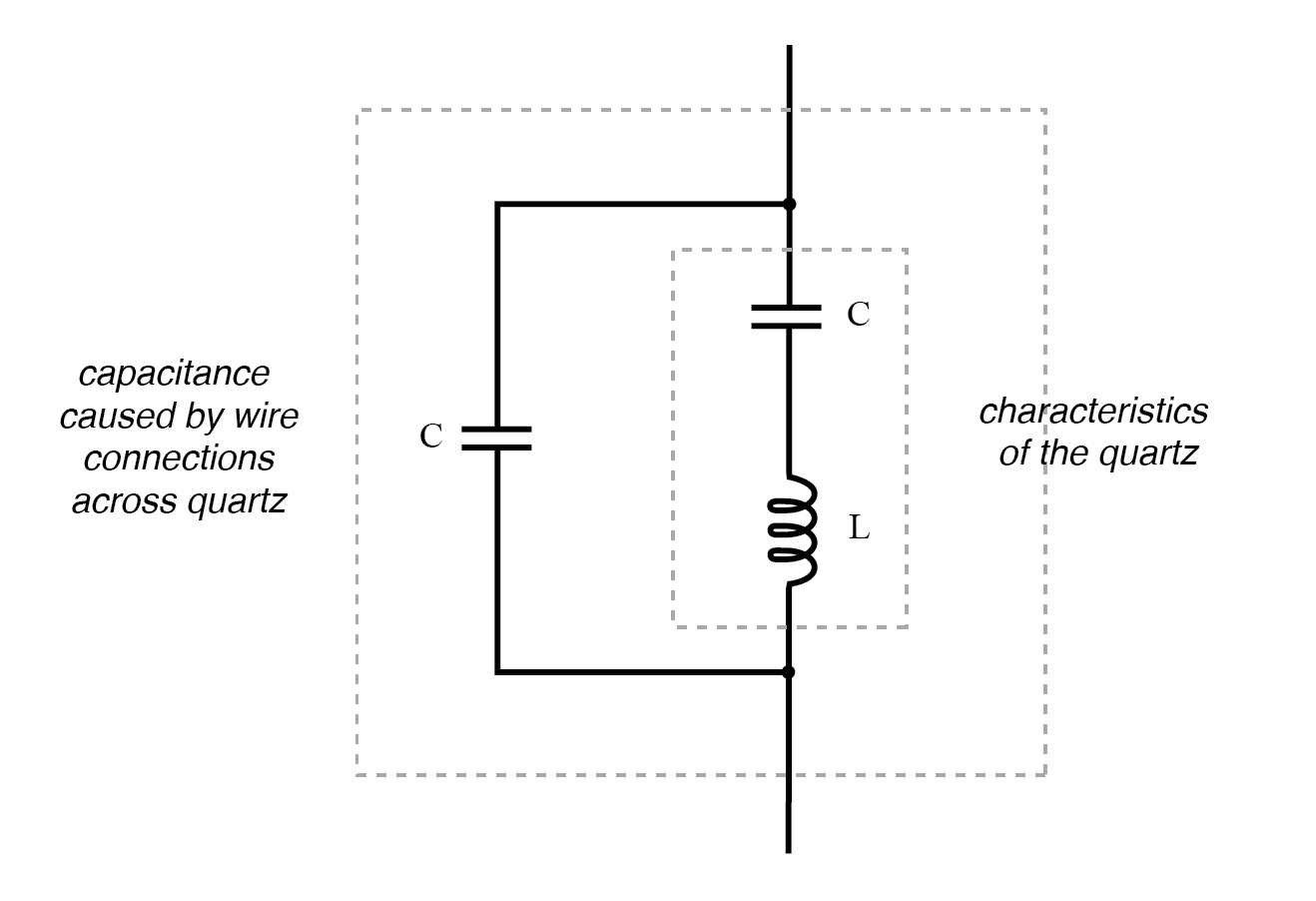
Sirkuit setara kristal kuarsa.

"Kapasitas" dan "induktansi" yang ditunjukkan secara seri hanyalah ekivalen listrik dari sifat resonansi mekanik kuarsa:mereka tidak ada sebagai komponen diskrit di dalam kristal. Kapasitansi yang ditunjukkan secara paralel karena sambungan kabel melintasi badan kuarsa dielektrik (penyekat) adalah nyata, dan ini memiliki efek pada respons resonansi seluruh sistem.

Diskusi lengkap tentang dinamika kristal tidak diperlukan di sini, tetapi yang perlu dipahami tentang kristal adalah kesetaraan rangkaian resonansi ini dan bagaimana hal itu dapat dimanfaatkan dalam rangkaian osilator untuk mencapai tegangan keluaran dengan frekuensi yang stabil dan diketahui.

Kristal, sebagai elemen resonansi, biasanya memiliki “Q” (kualitas yang jauh lebih tinggi ) nilai dari rangkaian tangki yang dibangun dari induktor dan kapasitor, terutama karena relatif tidak adanya resistansi nyasar, membuat frekuensi resonansinya sangat pasti dan presisi.

Karena frekuensi resonansi hanya bergantung pada sifat fisik kuarsa (zat yang sangat stabil, secara mekanis), variasi frekuensi resonansi dari waktu ke waktu dengan kristal kuarsa sangat, sangat rendah. Beginilah cara gerakan kuarsa jam tangan memperoleh akurasi tinggi:melalui osilator elektronik yang distabilkan oleh aksi resonansi kristal kuarsa.

Namun, untuk aplikasi laboratorium, stabilitas frekuensi yang lebih besar mungkin diinginkan. Untuk mencapai hal ini, kristal tersebut dapat ditempatkan di lingkungan yang stabil suhunya (biasanya oven), sehingga menghilangkan kesalahan frekuensi karena ekspansi termal dan kontraksi kuarsa.

Namun, untuk standar frekuensi tertinggi, tidak ada yang ditemukan sejauh ini yang melampaui akurasi atom tunggal yang beresonansi. Ini adalah prinsip yang disebut jam atom , yang menggunakan atom merkuri (atau cesium) yang tersuspensi dalam ruang hampa, tereksitasi oleh energi luar untuk beresonansi pada frekuensi uniknya sendiri.

Frekuensi yang dihasilkan dideteksi sebagai sinyal gelombang radio dan yang membentuk dasar untuk jam paling akurat yang dikenal umat manusia. Laboratorium standar nasional di seluruh dunia memelihara beberapa jam yang sangat akurat ini, dan menyiarkan sinyal frekuensi berdasarkan getaran atom tersebut agar para ilmuwan dan teknisi dapat menyetel dan menggunakannya untuk tujuan kalibrasi frekuensi.

Bagian Praktis

Sekarang kita masuk ke bagian praktis:setelah kita memiliki sumber frekuensi yang akurat, bagaimana kita membandingkannya dengan frekuensi yang tidak diketahui untuk mendapatkan pengukuran?

Salah satu caranya adalah dengan menggunakan CRT sebagai alat pembanding frekuensi. Tabung Sinar Katoda biasanya memiliki sarana untuk membelokkan berkas elektron pada sumbu horizontal maupun vertikal.

Jika pelat logam digunakan untuk membelokkan elektron secara elektrostatis, maka akan ada sepasang pelat di sebelah kiri dan kanan berkas serta sepasang pelat di atas dan di bawah berkas seperti pada gambar di bawah.

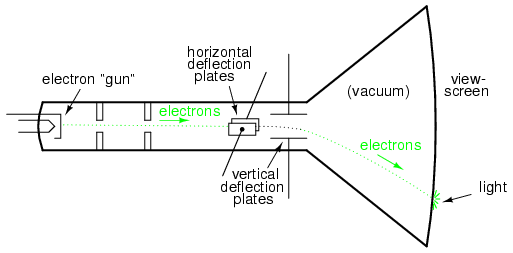
Tabung sinar katoda (CRT) dengan pelat defleksi vertikal dan horizontal.

Jika kita mengizinkan satu sinyal AC untuk membelokkan sinar ke atas dan ke bawah (menghubungkan sumber tegangan AC ke pelat defleksi "vertikal") dan sinyal AC lain untuk membelokkan sinar ke kiri dan ke kanan (menggunakan pasangan pelat defleksi lainnya), pola akan diproduksi di layar CRT yang menunjukkan rasio dari dua frekuensi AC ini.

Pola-pola ini disebut figur Lissajous dan merupakan cara umum pengukuran frekuensi komparatif dalam elektronik.

Jika kedua frekuensi tersebut sama, kita akan memperoleh gambar sederhana pada layar CRT, bentuk gambar tersebut bergantung pada pergeseran fasa antara dua sinyal AC. Berikut adalah contoh gambar Lissajous untuk dua sinyal gelombang sinus dengan frekuensi yang sama, ditunjukkan seperti yang akan muncul di muka osiloskop (alat pengukur tegangan AC yang menggunakan CRT sebagai “gerakannya”).

Gambar pertama adalah sosok Lissajous yang dibentuk oleh dua tegangan AC yang sefasa sempurna satu sama lain:

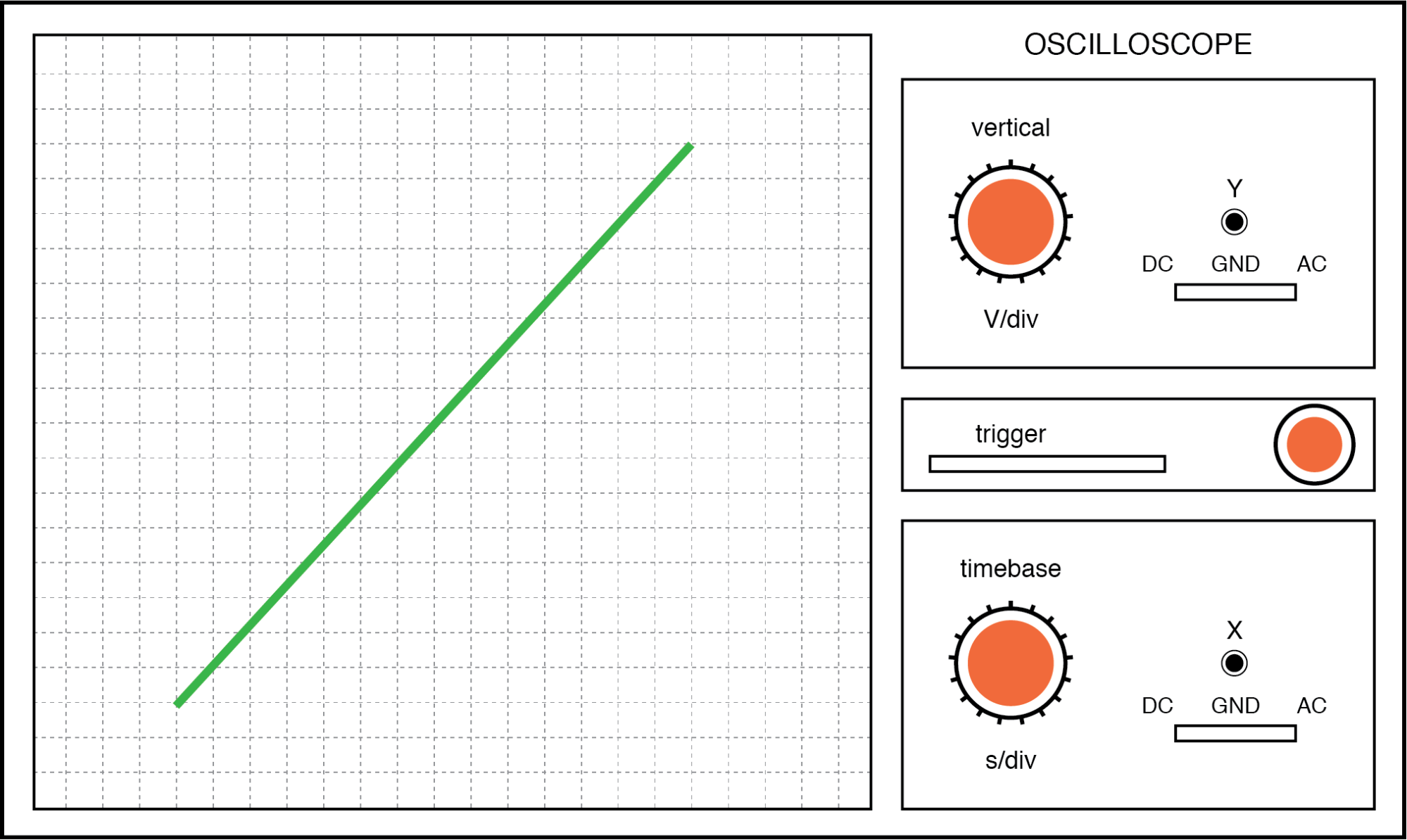
Angka Lissajous:frekuensi yang sama, pergeseran fase nol derajat.

Jika kedua tegangan AC tidak sefase, tidak akan terbentuk garis lurus. Sebaliknya, sosok Lissajous akan tampak seperti oval, menjadi lingkaran sempurna jika pergeseran fasa tepat 90° antara dua sinyal, dan jika amplitudonya sama:

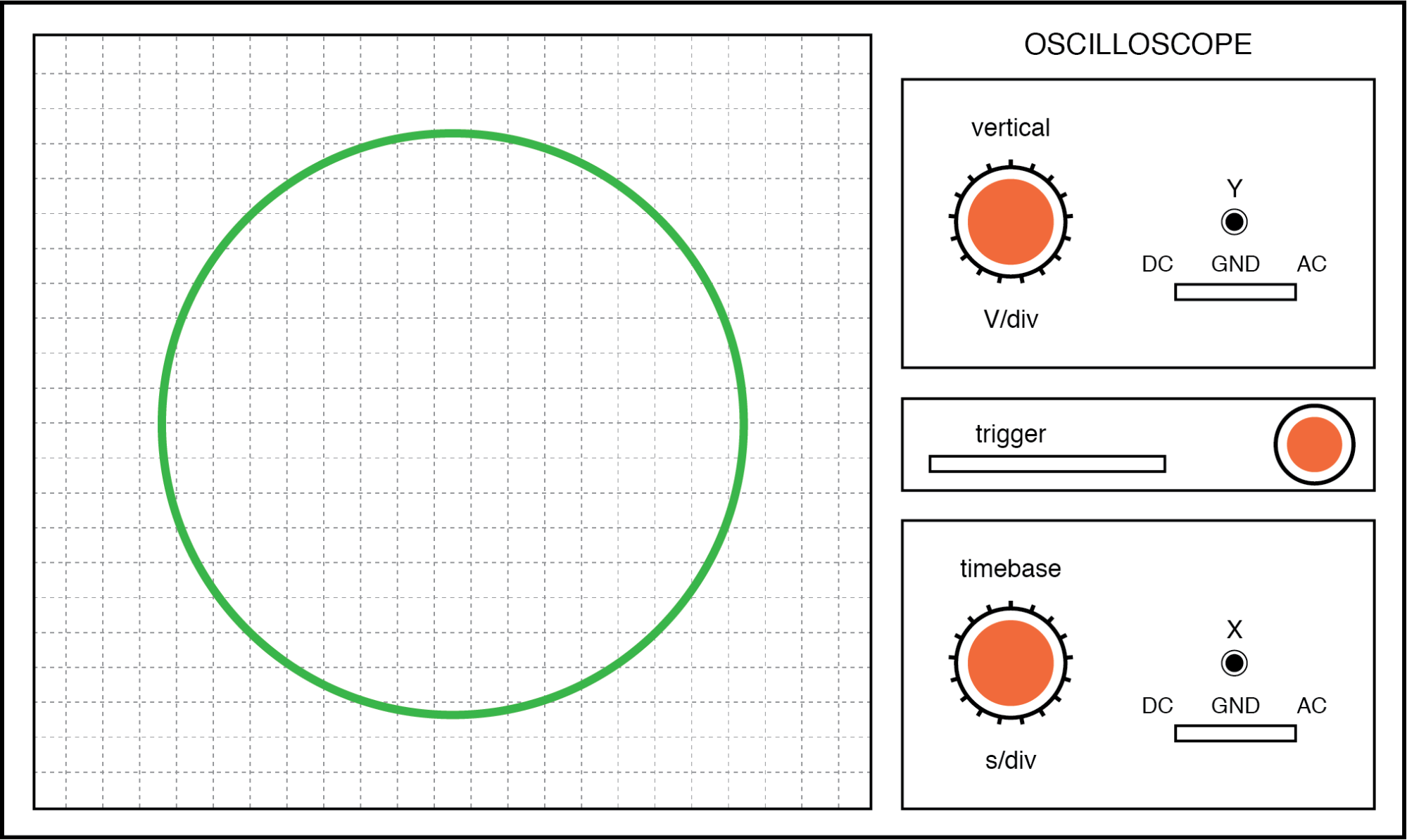
Angka Lissajous:frekuensi yang sama, pergeseran fase 90 atau 270 derajat.

Akhirnya, jika dua sinyal AC secara langsung berlawanan satu sama lain dalam fase (pergeseran 180 °), kita akan berakhir dengan garis lagi, hanya saja kali ini akan berorientasi pada arah yang berlawanan:

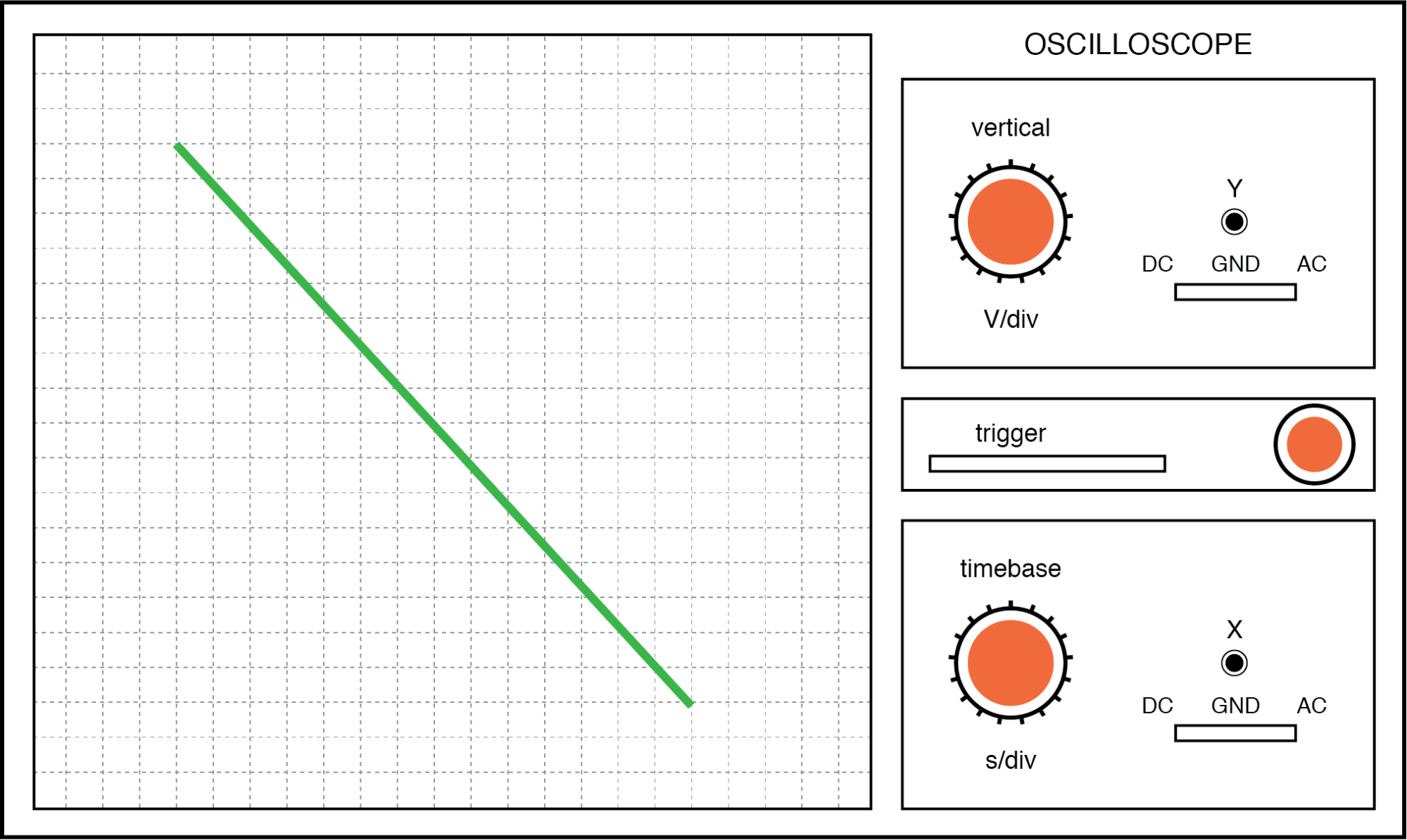
Angka Lissajous:frekuensi yang sama, pergeseran fasa 180 derajat.

Ketika kita dihadapkan dengan frekuensi sinyal yang tidak sama, angka Lissajous menjadi sedikit lebih kompleks. Perhatikan contoh berikut dan diberikan rasio frekuensi vertikal/horizontal:

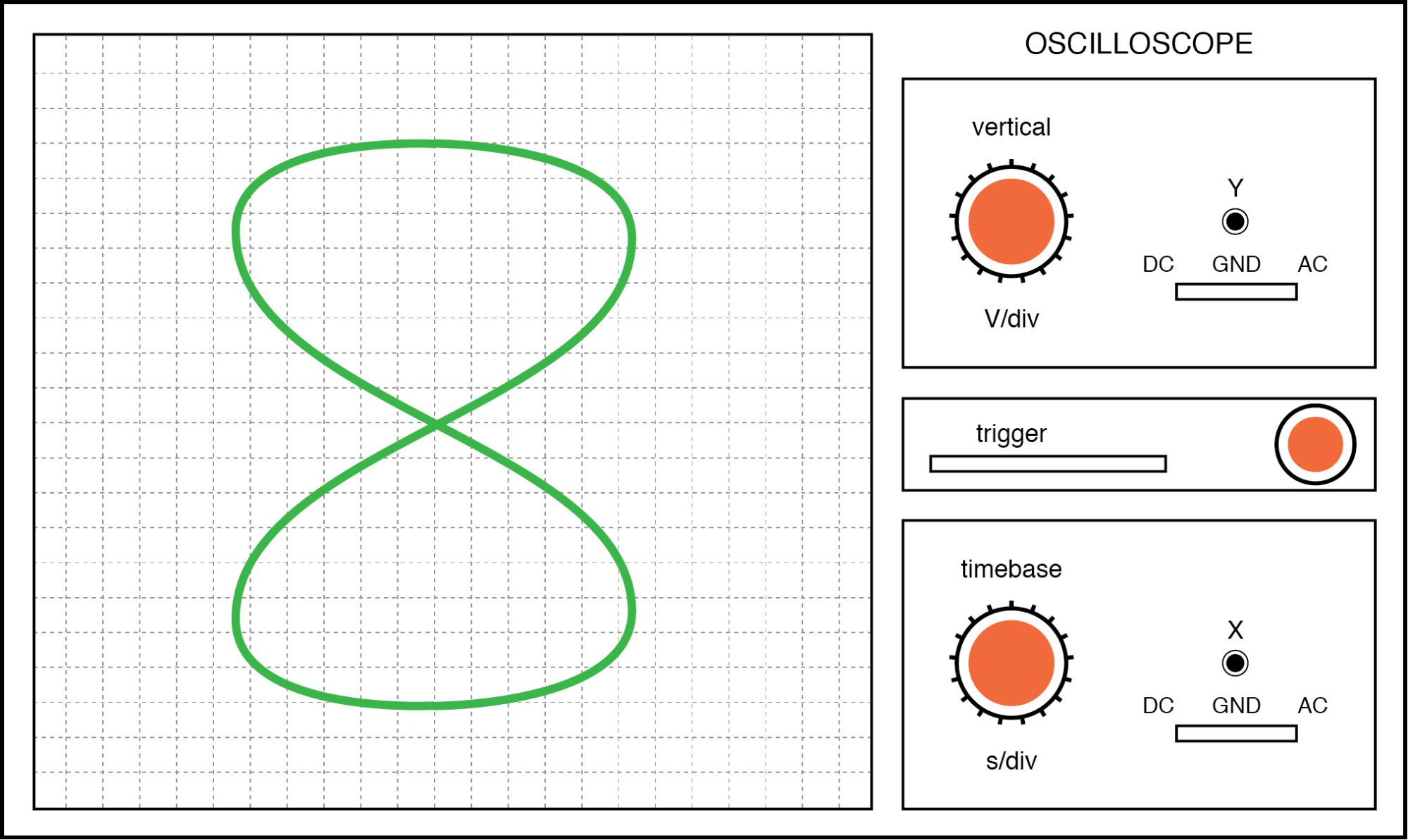
Angka Lissajous:Frekuensi horizontal dua kali frekuensi vertikal.

Semakin kompleks rasio antara frekuensi horizontal dan vertikal, semakin kompleks sosok Lissajous. Perhatikan ilustrasi rasio frekuensi 3:1 antara horizontal dan vertikal berikut ini:

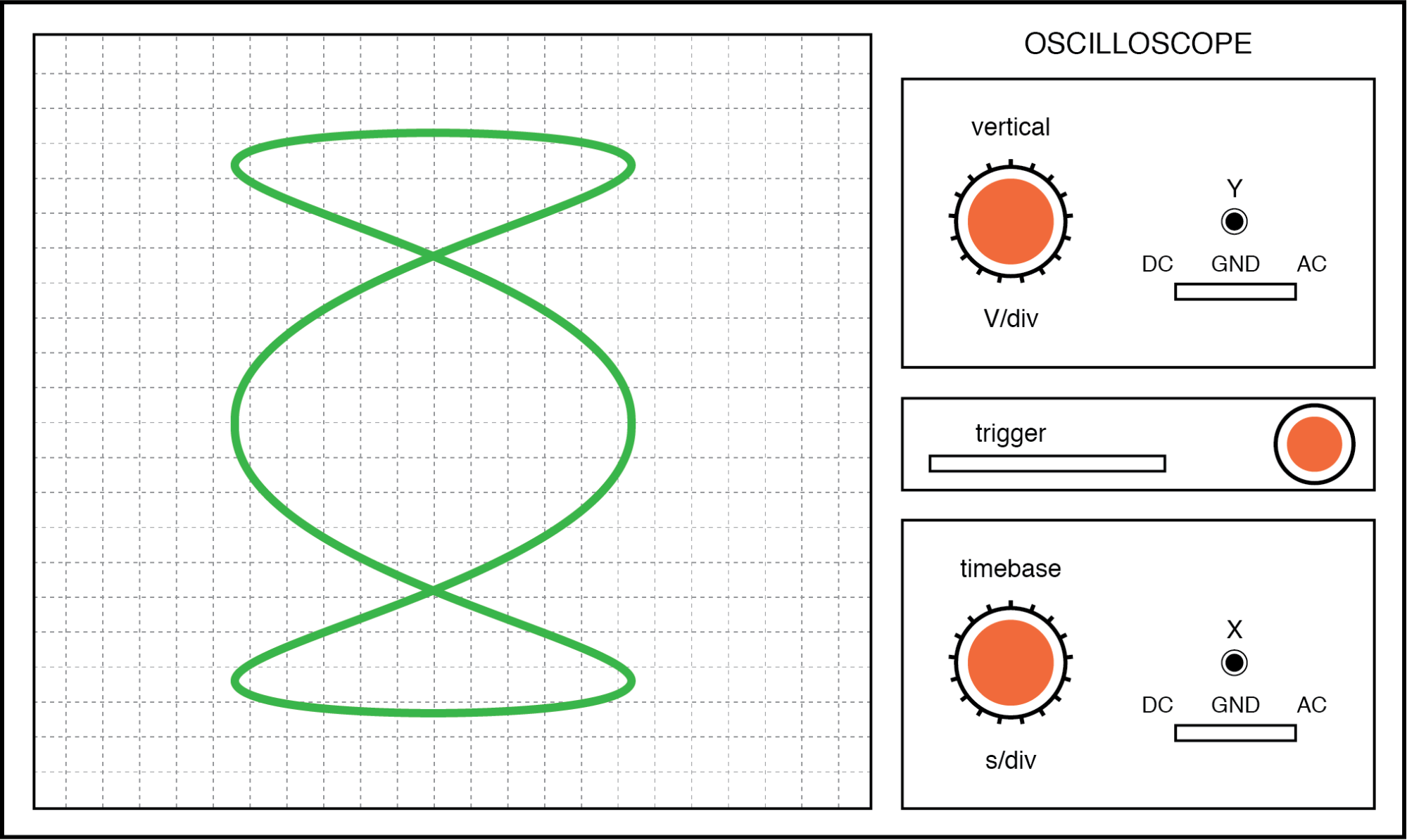
Angka Lissajous:Frekuensi horizontal tiga kali lipat frekuensi vertikal.

. . . dan rasio frekuensi 3:2 (horizontal =3, vertikal =2) pada gambar di bawah.

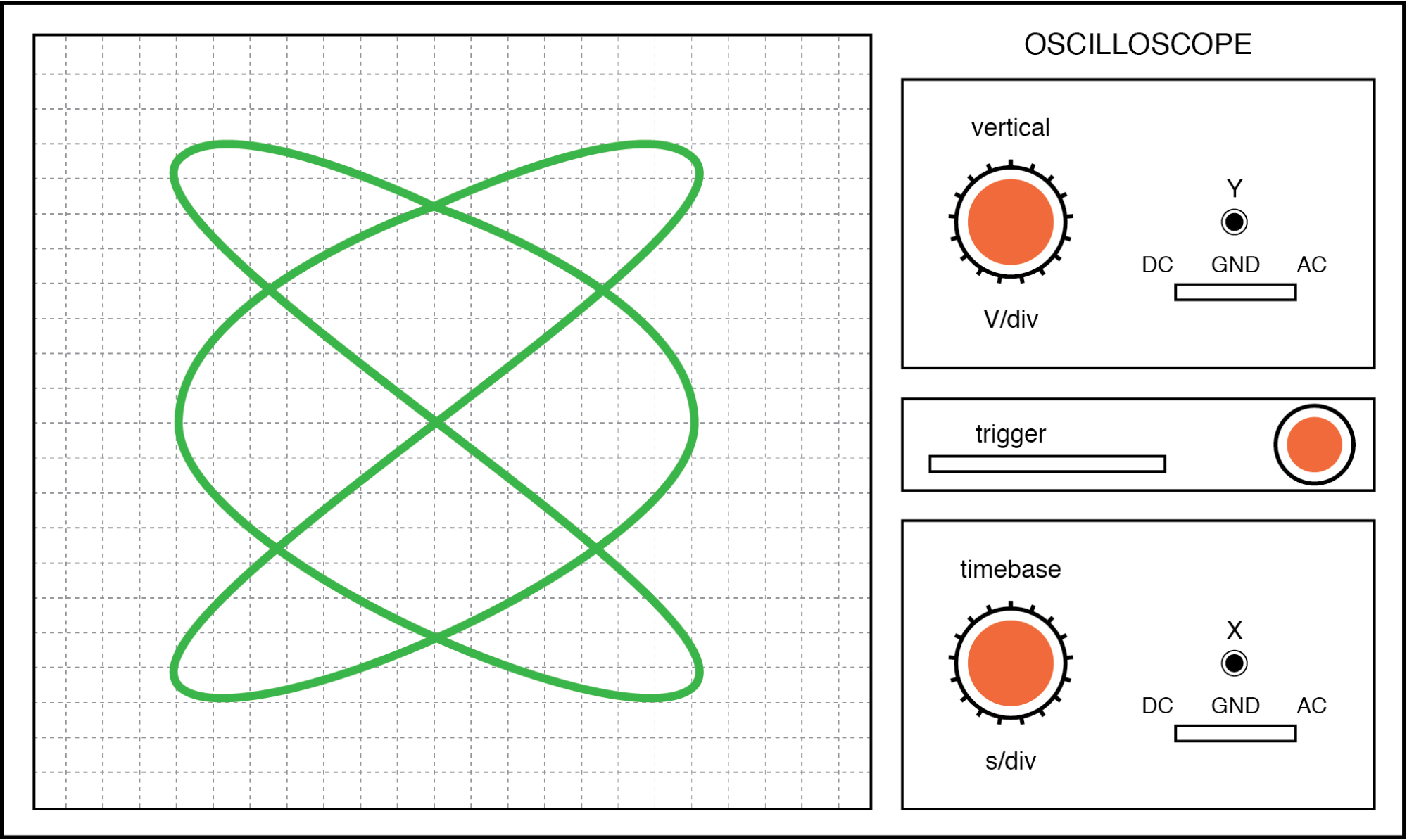
Angka Lissajous:Rasio frekuensi horizontal/vertikal adalah 3:2.

Dalam kasus di mana frekuensi dari dua sinyal AC tidak persis rasio sederhana satu sama lain (tapi dekat), sosok Lissajous akan tampak "bergerak," perlahan mengubah orientasi sebagai sudut fase antara dua bentuk gelombang berguling antara 0 ° dan 180°.

Jika dua frekuensi terkunci dalam rasio bilangan bulat yang tepat antara satu sama lain, sosok Lissajous akan stabil di layar tampilan CRT.

Fisika angka Lissajous membatasi kegunaannya sebagai teknik perbandingan frekuensi untuk kasus di mana rasio frekuensi adalah nilai bilangan bulat sederhana (1:1, 1:2, 1:3, 2:3, 3:4, dll.).

Terlepas dari keterbatasan ini, angka Lissajous adalah alat perbandingan frekuensi yang populer di mana pun ada standar frekuensi yang dapat diakses (generator sinyal).

TINJAUAN:

• Beberapa pengukur frekuensi bekerja berdasarkan prinsip resonansi mekanis, yang menunjukkan frekuensi melalui osilasi relatif di antara serangkaian "buluh" yang disetel secara unik yang diguncang pada frekuensi yang diukur.
• Pengukur frekuensi lainnya menggunakan sirkuit resonansi listrik (biasanya sirkuit tangki LC) untuk menunjukkan frekuensi. Satu atau kedua komponen dibuat agar dapat disetel, dengan kenop penyesuaian yang dikalibrasi secara akurat, dan pengukur sensitif dibaca untuk mengetahui tegangan atau arus maksimum pada titik resonansi.
• Frekuensi dapat diukur dengan cara komparatif, seperti halnya saat menggunakan CRT untuk menghasilkan angka Lissajous. Sinyal frekuensi referensi dapat dibuat dengan tingkat akurasi yang tinggi oleh rangkaian osilator menggunakan kristal kuarsa sebagai perangkat resonansi. Untuk presisi ultra, standar sinyal jam atom (berdasarkan frekuensi resonansi atom individu) dapat digunakan.