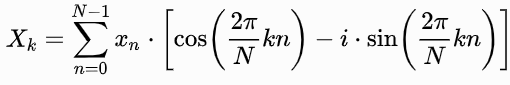Menghitung Transformasi Fourier Cepat pada LPC55S69 MCU

Artikel ini menyelidiki Transform Engine, bagian lain dari PowerQuad, yang memungkinkan MCU LPC55S69 menghitung Fast Fourier Transform (FFT).

Mikrokontroler LPC55S69 NXP berisi banyak fitur yang membuatnya cocok untuk berbagai aplikasi. MCU LPC55S69 dan unit PowerQuad-nya menyertakan komponen unik — Biquad dan Transform Engines — yang digunakan untuk menyelesaikan berbagai tugas, membiarkan inti CPU utama bebas untuk hal lain.

Artikel sebelumnya, Memahami Penyaringan Digital dengan Mikrokontroler Tertanam, mengeksplorasi berbagai metode yang banyak digunakan untuk menyaring dan memproses sampel data dalam domain waktu. Untuk itu, digunakan mesin Biquad dari unit PowerQuad LPC55S69.

Artikel ini menyelidiki Transform Engine, bagian lain dari PowerQuad, yang memungkinkan MCU LPC55S69 menghitung Fast Fourier Transform (FFT).

Memahami Transformasi Fourier Diskrit

Ketika berhadapan dengan pengukuran sehari-hari seperti panjang dan suhu, ada seperangkat alat untuk menentukan ukuran dan suhu benda tertentu yang diukur. Untuk sinyal domain waktu, pilihan alat ukur mungkin tidak begitu jelas. Perhatikan contoh sinyal berikut yang diberikan pada Gambar 1.

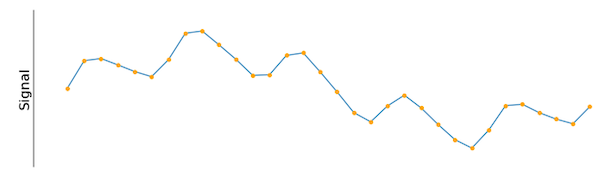
Gambar 1. Sinyal input disampel pada interval konstan.

Bagaimana sinyal ini dapat diukur, dipahami, dan dijelaskan? Pilihan yang mungkin bisa berupa amplitudo, frekuensi, atau beberapa nilai yang dihitung dengan metode dari statistik. Salah satu cara untuk memulai adalah dengan mengukur sinyal yang diinginkan terhadap gelombang kosinus yang diketahui, ditunjukkan pada Gambar 2.

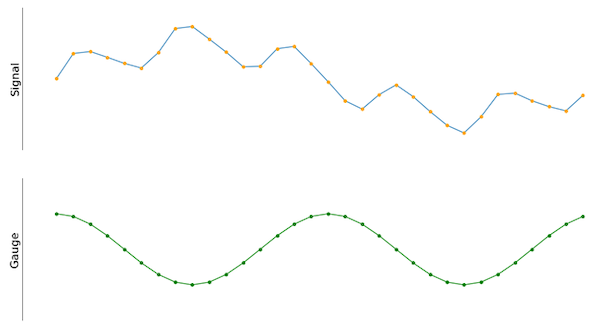
Gambar 2. Sinyal input di sebelah sinyal pengukur kosinus. Keduanya memiliki jumlah sampel yang sama.

Karena amplitudo dan frekuensi gelombang kosinus dapat dengan mudah diperbaiki dan oleh karena itu diidentifikasi, dimungkinkan untuk membandingkan gelombang kosinus dengan sinyal input. Jika dilakukan dengan benar, nilai hasil perkalian titik antara sinyal input dan gelombang kosinus mengkuantifikasi seberapa besar korelasi sinyal input dengan pengukur. Untuk itu, masuk akal untuk menganggap sinyal input dan gauge sebagai array input diskrit dengan panjang yang sama, dan menjadi mudah untuk menghitung produk titik.

Hasilnya adalah skalar, dan besarnya sebanding dengan seberapa baik sinyal input berkorelasi dengan sinyal pengukur kosinus. Operasi produk titik bermuara pada banyak operasi perkalian dan penambahan — operasi yang sama dibahas dalam Memahami Penyaringan Digital dengan Mikrokontroler Tertanam.

Metode ini dengan cepat memberikan hasil yang baik. Namun, ada kasus tertentu yang tidak berhasil saat menerapkan metode ini. Jika sinyal input adalah gelombang kosinus dengan frekuensi yang sama dengan pengukur, tetapi fasenya bergeser 90 derajat terhadap pengukur, keluaran dari metode yang disebutkan di atas akan menjadi nol. Dengan inspeksi visual, tampaknya masih ada korelasi antara pengukur dan sinyal input tetapi ada detail yang perlu kami perhitungkan.

Gambar 3. Sinyal pengukur yang baru mengalami pergeseran fase sebesar 90 derajat dibandingkan dengan yang lama.

Perilaku ini dapat dibandingkan dengan mengukur "panjang" secarik kertas tipis. Saat menggunakan penggaris untuk menentukan panjang satu sisi potongan kertas, panjang kertas mungkin 10 inci dan lebar satu inci. Kedua angka itu benar, tetapi penggaris harus diputar 90 derajat untuk mendapatkan kedua pengukuran. Kedua angka tersebut secara teknis benar dan kita dapat menggunakannya bersama-sama untuk mendapatkan “ukuran” (panjang dan lebar) kertas kita yang sebenarnya. Untuk mengatasi masalah ini dalam hal sinyal input kami, pengukur kedua dapat digunakan, seperti yang terlihat pada Gambar 4.

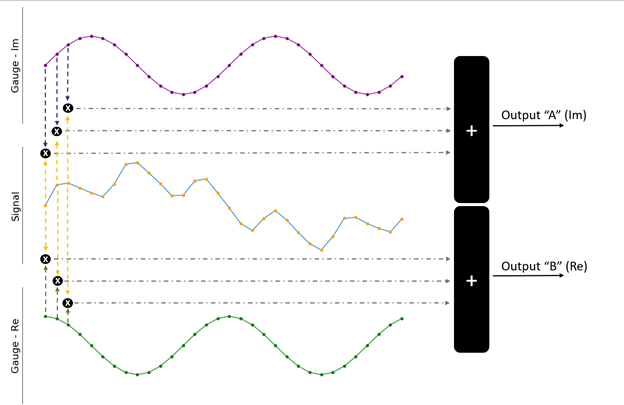
Gambar 4. Kedua sinyal pengukur dapat digunakan untuk mengukur sinyal input dengan lebih baik.

Satu-satunya perbedaan antara kedua pengukur (ditunjukkan dalam warna ungu dan hijau) adalah pergeseran fase 90 derajat. Dalam analogi sebelumnya, ini setara dengan memutar penggaris. Produk titik dihitung antara sinyal input dan masing-masing pengukur untuk mendapatkan output akhir. Hasil ini menghasilkan dua nilai A dan B, masing-masing berisi seberapa baik input berkorelasi dengan salah satu pengukur. Biasanya, mereka dianggap sebagai bilangan kompleks tunggal:

keluaran =B + i * A

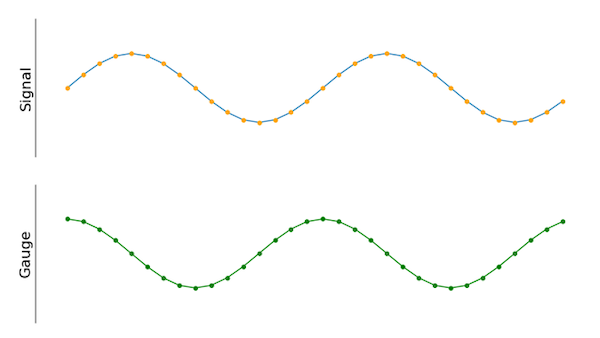
Langkah selanjutnya adalah membandingkan sinyal input dengan rentang pengukur dengan frekuensi yang berbeda (Gambar 5).

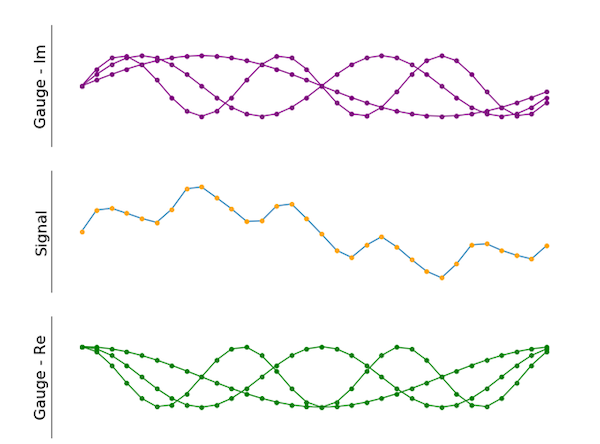
Gambar 5. Beberapa pengukur dapat diterapkan juga. Yang hijau bergeser 90 derajat dibandingkan dengan yang ungu.

Seperti yang ditunjukkan gambar, hasil akhir menggabungkan beberapa pengukur yang berbeda. Bagian imajiner (ditunjukkan dalam warna ungu) adalah fase yang digeser 90 derajat dibandingkan dengan sinyal hijau (bagian nyata), seperti pada contoh dua pengukur yang ditunjukkan di atas. Tidak ada batasan jumlah pengukur yang berbeda.

Menggunakan teknik ini — disebut Discrete Fourier Transform (DFT) — menghasilkan pembangkitan spektrum keluaran pada semua frekuensi yang diinginkan untuk suatu masalah. Dimungkinkan untuk menyatakan teknik secara matematis sebagai berikut:

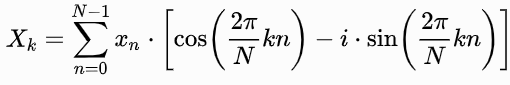
Persamaan 1. Deskripsi matematis DFT.

Dimana N adalah jumlah sampel dalam sinyal input dan k adalah frekuensi pengukur referensi (co)sinus.

Keterbatasan Transformasi Fourier Cepat (FFT)

FFT adalah cara penghitungan DFT yang efisien secara numerik yang membutuhkan lebih sedikit operasi perkalian dan penambahan dibandingkan dengan metode yang dibahas di atas. Namun, ada beberapa batasan pada input:

1. Panjang input harus pangkat dua.
2. Panjang input yang berubah-ubah dan jarak frekuensi dalam output tidak diperbolehkan. Tempat keluaran diberi jarak dengan laju sampel sinyal masukan dibagi dengan jumlah sampel dalam masukan. Jika inputnya, misalnya, sinyal 256 titik yang diambil sampelnya pada 48 kHz, larik output sesuai dengan frekuensi yang ditempatkan pada 187 Hz (48.000 dibagi 256).
3. Bila input terdiri dari bilangan real (misalnya, sampel yang diperoleh dari ADC), outputnya simetris. Jika input, misalnya, terdiri dari 64 sampel, hasil FFT juga akan terdiri dari 64 bilangan kompleks. Namun, paruh kedua larik keluaran berisi konjugat kompleks dari paruh pertama.

Menggunakan Mesin FFT PowerQuad

Perhitungan di balik operasi DFT/FFT dapat dilakukan dengan operasi perkalian dan penambahan sederhana, yang ideal untuk mengalihdayakan operasi matematika ke koprosesor khusus, seperti PowerQuad pada LPC55S69 MCU. Karena itu, inti CPU utama bebas untuk mengerjakan tugas lain.

Memanfaatkan mesin FFT PowerQuad adalah proses yang sederhana, dan SDK resmi dilengkapi dengan contoh proyek yang menunjukkan fitur coprocessing. Salah satu contoh khususnya, yang disebut powerquad_transform, menunjukkan proses perhitungan FFT.

File powerquad_transform.c berisi beberapa fungsi yang menguji mode mesin FFT yang berbeda. Salah satunya adalah fungsi PQ_RFFTFixed16Example. Contoh ini menginisialisasi PowerQuad untuk menerima data integer 16-bit. Data titik-mengambang harus dikonversi ke nilai titik-tetap terlebih dahulu, karena mesin transformasi PowerQuad hanya mendukung bilangan bulat.

FILTER_INPUT_LEN mendefinisikan jumlah sampel input. Larik keluaran dua kali panjangnya karena perlu menyimpan bagian real dan imajiner dari nilai yang dihasilkan.

Gambar 6. Bagian kode ini mendefinisikan data uji dan hasil yang diharapkan.

Array terakhir berisi data uji untuk memverifikasi hasil. Perhatikan bagaimana paruh kedua larik berisi konjugat kompleks seperti yang dinyatakan di atas. Selanjutnya, konjugatnya tidak sama (misalnya pasangan 76,-50, dan 77,49). Bagaimanapun, setelah data diinisialisasi, struktur data berikut digunakan untuk mengonfigurasi PowerQuad:

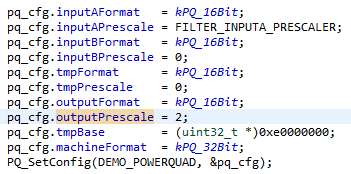
Gambar 7. Bagian dari contoh program ini mengonfigurasi dan menginisialisasi unit PowerQuad.

Penting untuk menurunkan skala input untuk mencegah algoritme meluap. Proses ini terjadi pada baris kedua pada gambar di atas. FILTER_INPUTA_PRESCALER disetel ke lima karena ada 32 (dua pangkat lima) sampel. Pra-penskalaan adalah fitur perangkat keras lain dari PowerQuad, dan kemungkinan alasan ketidaktepatan yang diamati dalam hasil pengujian yang diharapkan.

Setelah semuanya diatur, lokasi area input dan output diteruskan ke unit PowerQuad, yang terjadi dalam fungsi PQ_transformRFFT. Metode ini menetapkan beberapa register konfigurasi dan memulai PowerQuad dengan menulis ke register kontrol. Dalam contoh ini, CPU menunggu PowerQuad selesai. Menunggu tidak selalu diperlukan, dan PowerQuad dapat melakukan penghitungan secara asinkron saat CPU melakukan tugas lain.

Gunakan PowerQuad untuk Operasi Matematika

PowerQuad adalah koprosesor untuk operasi matematika kompleks yang tersedia di berbagai perangkat seri LPC5500 MCU. Ini termasuk mesin khusus untuk menghitung FFT secara efisien, yang dapat dilakukan secara independen dari inti CPU utama. SDK untuk LPC55S69 MCU berisi contoh cara menyiapkan dan menggunakan PowerQuad.

Halaman Komunitas NXP berisi informasi ekstensif, diskusi, dan artikel yang berpusat di sekitar MCU LPC55S69.

Artikel Industri adalah bentuk konten yang memungkinkan mitra industri untuk berbagi berita, pesan, dan teknologi yang bermanfaat dengan pembaca All About Circuits dengan cara yang tidak sesuai dengan konten editorial. Semua Artikel Industri tunduk pada pedoman editorial yang ketat dengan tujuan menawarkan kepada pembaca berita, keahlian teknis, atau cerita yang bermanfaat. Sudut pandang dan pendapat yang diungkapkan dalam Artikel Industri adalah milik mitra dan belum tentu milik All About Circuits atau penulisnya.