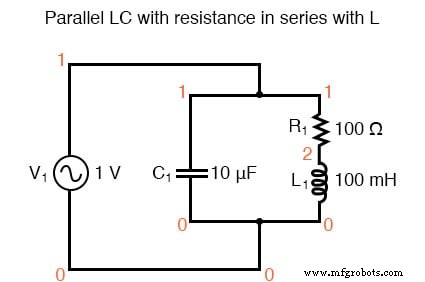
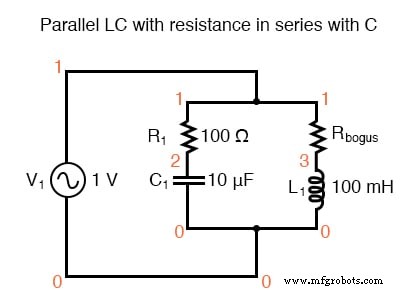
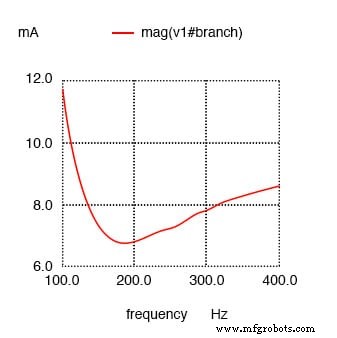
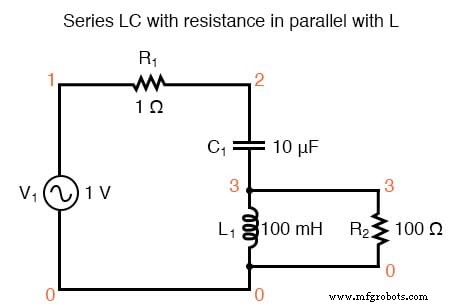
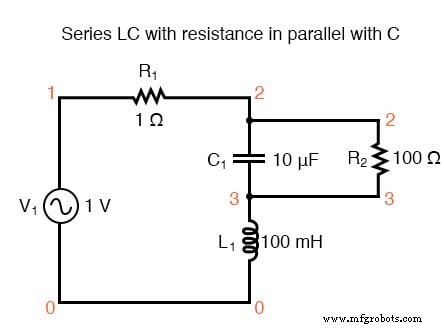
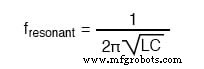Dan akhirnya, rangkaian LC seri dengan hambatan yang signifikan secara paralel dengan kapasitor Resonansi yang digeser ditunjukkan di bawah ini.
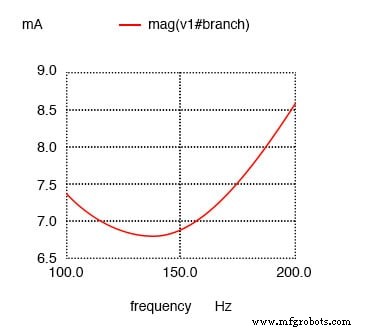
sirkuit resonansi v1 1 0 ac 1 dosa r1 1 2 1 c1 2 3 10u r2 2 3 100 l1 3 0 100m .ac lin 20 100 200 .plot ac i(v1) .akhir Arus maksimum pada 136,8 Hz, bukan 159,2 Hz!
Hasil:
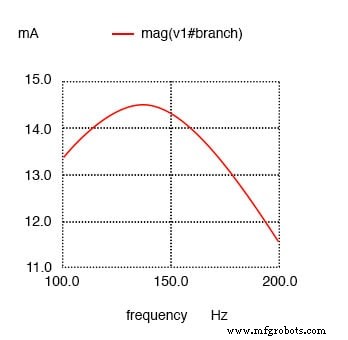
Resistansi paralel dengan C dalam rangkaian resonansi seri menggeser arus maksimum dari 159,2 Hz yang dihitung menjadi sekitar 136,8 Hz.
Antiresonansi di Sirkuit LC
Kecenderungan resistensi tambahan untuk membelokkan titik di mana impedansi mencapai maksimum atau minimum dalam rangkaian LC disebut antiresonansi . Pengamat yang cerdik akan melihat pola antara empat contoh SPICE yang diberikan di atas, dalam hal bagaimana hambatan mempengaruhi puncak resonansi suatu rangkaian:
Sirkuit LC paralel (“tangki”):
- R seri dengan L:frekuensi resonansi bergeser turun
- R seri dengan C:frekuensi resonansi bergeser naik
Sirkuit LC seri:
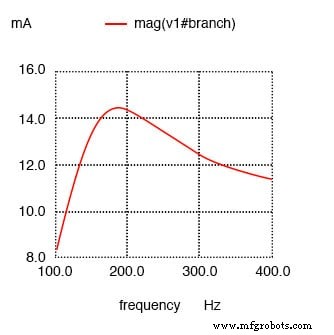
- R paralel dengan L:frekuensi resonansi bergeser naik
- R paralel dengan C:frekuensi resonansi bergeser turun
Sekali lagi, ini menggambarkan sifat komplementer dari kapasitor dan induktor:bagaimana resistansi secara seri dengan yang satu menciptakan efek antiresonansi yang setara dengan resistansi secara paralel dengan yang lain. Jika Anda melihat lebih dekat ke empat contoh SPICE yang diberikan, Anda akan melihat bahwa frekuensi digeser oleh jumlah yang sama , dan bahwa bentuk grafik komplementer adalah bayangan cermin satu sama lain!
Antiresonansi adalah efek yang harus diperhatikan oleh perancang sirkuit resonansi. Persamaan untuk menentukan "pergeseran" antiresonansi rumit, dan tidak akan dibahas dalam pelajaran singkat ini. Siswa awal elektronika harus cukup memahami bahwa efek itu ada, dan apa kecenderungan umumnya.
Efek Kulit
Perlawanan tambahan di sirkuit LC bukanlah masalah akademis. Meskipun dimungkinkan untuk memproduksi kapasitor dengan resistansi yang tidak diinginkan yang dapat diabaikan, induktor biasanya diganggu dengan sejumlah besar resistansi karena panjang kabel yang digunakan dalam konstruksinya.
Terlebih lagi, resistansi kawat cenderung meningkat seiring dengan meningkatnya frekuensi, karena fenomena aneh yang dikenal sebagai efek kulit di mana arus AC cenderung dikecualikan dari perjalanan melalui pusat kabel, sehingga mengurangi luas penampang efektif kabel.
Jadi, induktor tidak hanya memiliki resistansi, tetapi juga berubah, bergantung pada frekuensi perlawanan pada saat itu.
Menambahkan Resistansi di Sirkuit
Seolah-olah resistansi kawat induktor tidak cukup untuk menyebabkan masalah, kita juga harus menghadapi "kerugian inti" dari induktor inti besi, yang memanifestasikan dirinya sebagai resistansi tambahan di sirkuit.
Karena besi adalah penghantar listrik serta penghantar fluks magnet, perubahan fluks yang dihasilkan oleh arus bolak-balik melalui kumparan akan cenderung menginduksi arus listrik di dalam inti itu sendiri (arus eddy ).
Efek ini dapat dianggap seolah-olah inti besi transformator adalah semacam kumparan transformator sekunder yang memberi daya pada beban resistif:konduktivitas logam besi yang kurang sempurna. Efek ini dapat diminimalkan dengan inti yang dilaminasi, desain inti yang baik dengan bahan bermutu tinggi, tetapi tidak pernah sepenuhnya dihilangkan.
Sirkuit RLC
Satu pengecualian penting untuk aturan resistansi rangkaian yang menyebabkan pergeseran frekuensi resonansi adalah kasus rangkaian resistor-induktor-kapasitor (“RLC”) seri. Selama semua komponen dihubungkan secara seri satu sama lain, frekuensi resonansi rangkaian tidak akan terpengaruh oleh resistansi. Plot yang dihasilkan ditunjukkan di bawah ini.
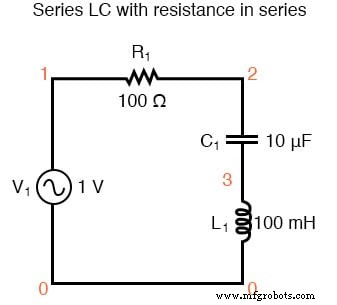
Seri LC dengan resistansi seri.
sirkuit rlc seri v1 1 0 ac 1 dosa r1 1 2 100 c1 2 3 10u l1 3 0 100m .ac lin 20 100 200 .plot ac i(v1) .akhir Arus maksimum pada 159,2 Hz sekali lagi!
Hasil:
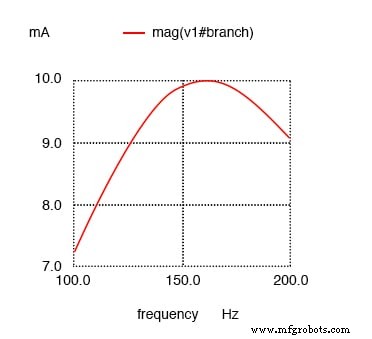
Resistensi dalam rangkaian resonansi seri meninggalkan arus maksimum pada 159,2 Hz yang dihitung, memperluas kurva.
Perhatikan bahwa puncak grafik saat ini tidak berubah dari rangkaian LC seri sebelumnya (yang memiliki resistansi token 1 di dalamnya), meskipun resistansi sekarang 100 kali lebih besar. Satu-satunya hal yang berubah adalah "ketajaman" kurva.
Jelas, rangkaian ini tidak beresonansi sekuat rangkaian dengan resistansi seri yang lebih kecil (disebut "kurang selektif"), tetapi setidaknya ia memiliki frekuensi alami yang sama!
Efek Peredam Antiresonansi
Perlu dicatat bahwa antiresonansi memiliki efek meredam osilasi sirkuit LC yang berjalan bebas seperti sirkuit tangki. Di awal bab ini kita melihat bagaimana kapasitor dan induktor yang terhubung langsung akan bertindak seperti bandul, menukar puncak tegangan dan arus seperti bandul yang menukar energi kinetik dan potensial.
Dalam rangkaian tangki yang sempurna (tanpa hambatan), osilasi ini akan berlanjut selamanya, sama seperti bandul tanpa gesekan akan terus berayun pada frekuensi resonansinya selamanya. Tetapi mesin tanpa gesekan sulit ditemukan di dunia nyata, begitu juga dengan sirkuit tangki tanpa kehilangan.
Energi yang hilang melalui resistansi (atau kerugian inti induktor atau gelombang elektromagnetik yang terpancar atau ...) dalam rangkaian tangki akan menyebabkan osilasi berkurang dalam amplitudo sampai tidak ada lagi. Jika ada kehilangan energi yang cukup di sirkuit tangki, itu akan gagal beresonansi sama sekali.
Efek peredam antiresonansi lebih dari sekadar rasa ingin tahu:ini dapat digunakan dengan cukup efektif untuk menghilangkan yang tidak diinginkan osilasi di sirkuit yang mengandung induktansi dan / atau kapasitansi nyasar, seperti yang dilakukan hampir semua sirkuit. Perhatikan rangkaian waktu tunda L/R berikut:(Gambar di bawah)
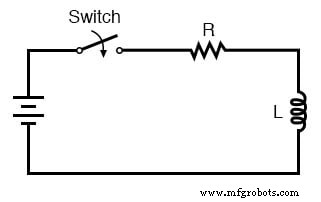
Sirkuit tunda waktu L/R
Ide rangkaian ini sederhana:untuk "mengisi" induktor saat sakelar ditutup. Laju pengisian induktor akan diatur oleh rasio L/R, yang merupakan konstanta waktu rangkaian dalam detik.
Namun, jika Anda membuat sirkuit seperti itu, Anda mungkin menemukan osilasi (AC) tegangan tak terduga di induktor saat sakelar ditutup. (Gambar di bawah) Mengapa demikian? Tidak ada kapasitor di sirkuit, jadi bagaimana kita bisa memiliki osilasi resonansi hanya dengan induktor, resistor, dan baterai?
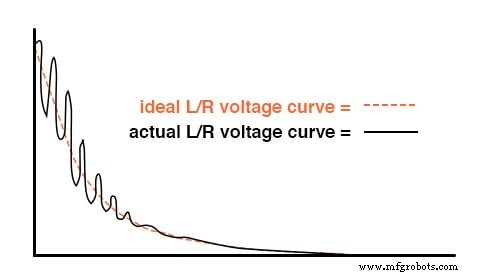
Induktor berdering karena resonansi dengan kapasitansi nyasar.
Semua induktor mengandung sejumlah kapasitansi nyasar karena celah isolasi belokan ke belokan dan belok ke inti. Juga, penempatan konduktor sirkuit dapat membuat kapasitansi menyimpang. Meskipun tata letak sirkuit yang bersih penting dalam menghilangkan sebagian besar kapasitansi yang menyimpang ini, akan selalu ada beberapa yang tidak dapat Anda hilangkan.
Jika ini menyebabkan masalah resonansi (osilasi AC yang tidak diinginkan), resistensi tambahan mungkin merupakan cara untuk memeranginya. Jika resistor R cukup besar, itu akan menyebabkan kondisi antiresonansi, membuang energi yang cukup untuk mencegah induktansi dan kapasitansi menyimpang dari mempertahankan osilasi untuk waktu yang lama.
Yang cukup menarik, prinsip menggunakan resistensi untuk menghilangkan resonansi yang tidak diinginkan adalah salah satu yang sering digunakan dalam desain sistem mekanis, di mana setiap objek bergerak dengan massa merupakan resonator potensial.
Aplikasi yang sangat umum dari ini adalah penggunaan peredam kejut di mobil. Tanpa peredam kejut, mobil akan memantul liar pada frekuensi resonansinya setelah menabrak gundukan apa pun di jalan. Tugas peredam kejut adalah memberikan efek antiresonansi yang kuat dengan membuang energi secara hidraulik (dengan cara yang sama seperti resistor membuang energi secara elektrik).
TINJAUAN:
- Resistensi tambahan ke sirkuit LC dapat menyebabkan kondisi yang dikenal sebagai antiresonansi , di mana efek impedansi puncak terjadi pada frekuensi selain frekuensi yang memberikan reaktansi kapasitif dan induktif yang sama.
- Resistensi yang melekat pada induktor dunia nyata dapat berkontribusi besar pada kondisi antiresonansi. Salah satu sumber resistensi tersebut adalah efek kulit , disebabkan oleh pengecualian arus AC dari pusat konduktor. Sumber lain adalah kerugian inti dalam induktor inti besi.
- Dalam rangkaian LC seri sederhana yang mengandung resistansi (sirkuit "RLC"), resistansi tidak menghasilkan antiresonansi. Resonansi masih terjadi ketika reaktansi kapasitif dan induktif sama.
LEMBAR KERJA TERKAIT: