MATLAB - Integrasi

Integrasi menangani dua jenis masalah yang pada dasarnya berbeda.

• Pada tipe pertama, turunan dari suatu fungsi diberikan dan kita ingin mencari fungsinya. Oleh karena itu, pada dasarnya kami membalikkan proses diferensiasi. Proses kebalikan ini dikenal sebagai anti-diferensiasi, atau menemukan fungsi primitif, atau menemukan integral tak tentu .

• Jenis masalah kedua melibatkan menjumlahkan jumlah yang sangat besar dari jumlah yang sangat kecil dan kemudian mengambil batas karena ukuran besaran mendekati nol, sedangkan jumlah suku cenderung tak terhingga. Proses ini mengarah pada definisi integral tak tentu .

Integral tertentu digunakan untuk mencari luas, volume, pusat gravitasi, momen inersia, kerja yang dilakukan oleh gaya, dan dalam berbagai aplikasi lainnya.

Menemukan Integral Tak Terbatas Menggunakan MATLAB

Menurut definisi, jika turunan dari suatu fungsi f(x) adalah f'(x), maka kita katakan bahwa integral tak tentu dari f'(x) terhadap x adalah f(x). Misalnya, karena turunan (terhadap x) dari x ² adalah 2x, kita dapat mengatakan bahwa integral tak tentu dari 2x adalah x ² .

Dalam simbol

f'(x ² ) =2x , oleh karena itu,

∫ 2xdx =x ² .

Integral tak tentu tidak unik, karena turunan dari x ² + c, untuk setiap nilai konstanta c, juga akan menjadi 2x.

Ini dinyatakan dalam simbol sebagai

∫ 2xdx =x ² + c .

Dimana, c disebut 'konstanta arbitrer'.

MATLAB menyediakan int perintah untuk menghitung integral dari suatu ekspresi. Untuk menurunkan ekspresi integral tak tentu dari suatu fungsi, kita tulis −

int(f);

Misalnya, dari contoh kita sebelumnya

syms x 
int(2*x)

MATLAB mengeksekusi pernyataan di atas dan mengembalikan hasil berikut

ans =
   x^2

Contoh 1

Dalam contoh ini, mari kita cari integral dari beberapa ekspresi yang umum digunakan. Buat file skrip dan ketik kode berikut di dalamnya

syms x n

int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)

Saat Anda menjalankan file, ini akan menampilkan hasil berikut

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

Contoh 2

Buat file skrip dan ketik kode berikut di dalamnya

syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))

int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))

int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

Perhatikan bahwa cantik fungsi mengembalikan ekspresi dalam format yang lebih mudah dibaca.

Saat Anda menjalankan file, ini akan menampilkan hasil berikut

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

Menemukan Integral Pasti Menggunakan MATLAB

Menurut definisi, integral tertentu pada dasarnya adalah limit dari suatu jumlah. Kami menggunakan integral tertentu untuk menemukan area seperti area antara kurva dan sumbu x dan area antara dua kurva. Integral tentu juga dapat digunakan dalam situasi lain, di mana kuantitas yang dibutuhkan dapat dinyatakan sebagai limit dari suatu penjumlahan.

int fungsi dapat digunakan untuk integrasi pasti dengan melewati batas yang ingin Anda hitung integralnya.

Untuk menghitung

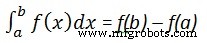
kami menulis,

int(x, a, b)

Misalnya, untuk menghitung nilai 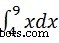kami menulis −

int(x, 4, 9)

MATLAB mengeksekusi pernyataan di atas dan mengembalikan hasil berikut

ans =
   65/2

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);

a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

Area: 

   32.500

Solusi alternatif dapat diberikan menggunakan fungsi quad() yang disediakan oleh Oktaf sebagai berikut −

pkg load symbolic
symbols

f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);

display('Area: '), disp(double(a));

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

Area: 
   32.500

Contoh 1

Mari kita hitung luas daerah yang dilingkupi antara sumbu x, dan kurva y =x ³ 2x+5 dan ordinat x =1 dan x =2.

Area yang dibutuhkan diberikan oleh

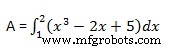
Buat file skrip dan ketik kode berikut

f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));

Saat Anda menjalankan file, ini akan menampilkan hasil berikut

a =
23/4
Area: 
   5.7500

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);

a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

Area: 

   5.7500

Solusi alternatif dapat diberikan menggunakan fungsi quad() yang disediakan oleh Oktaf sebagai berikut −

pkg load symbolic
symbols

x = sym("x");
f = inline("x^3 - 2*x +5");

[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));

Oktaf mengeksekusi kode dan mengembalikan hasil berikut

Area: 
   5.7500

Contoh 2

Cari luas di bawah kurva:f(x) =x ² cos(x) untuk 4 x 9.

Buat file skrip dan tulis kode berikut

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Saat Anda menjalankan file, MATLAB memplot grafik

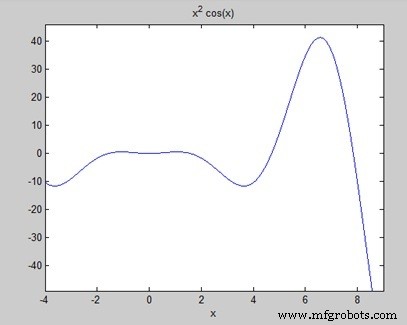
Outputnya diberikan di bawah ini

a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

Berikut ini adalah setara Oktaf dari perhitungan di atas

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));