Robot Euler Angles:Primer Esensial

Sulit untuk memahami rotasi robot, bukan? Euler Angles adalah rasa sakit di leher. Inilah primer penting untuk menghilangkan rasa sakit.

Orientasi! Mereka hanya membuatku ingin mencabuti rambutku. Jika Anda pernah harus memprogram pose akhir robot menggunakan koordinat dan rotasi, Anda akan tahu apa yang saya bicarakan.

Sekilas, mengatur pose end effector robot Anda tampak sederhana, bukan?

Anda cukup mengatakan “Saya ingin memindahkan alat robot ke ini lokasi dan saya ingin menunjuk ke ini arah.”

Secara intuitif, Anda tahu persis orientasi apa yang Anda inginkan dari alat tersebut. Namun, ketika menjelaskan orientasi menggunakan angka yang tepat, tiba-tiba tugas sederhana ini menjadi kacau balau.

Mengapa Orientasi Robot Sulit Dipahami

Sangat mudah untuk mendeskripsikan koordinat X, Y, Z (translasi) dari alat robot.

Untuk mendeskripsikan terjemahan, Anda cukup memasukkan koordinat — mis. Titik[X, Y, Z] =[100, 1000, 1500] mm — dan hanya ada satu lokasi yang dapat dirujuk, dengan asumsi Anda menggunakan referensi dasar yang sama. Ini hanya dapat berarti 100 mm sepanjang sumbu X, 1 meter sepanjang sumbu Y dan 1,5 meter sepanjang sumbu Z.

Tetapi, bagaimana Anda menggambarkan orientasi alat ini?

Anda bisa mengatakan:
Rotation[XYZ] =[5, 45, 15]°
namun, Anda bisa juga mengatakan (membulatkan angka)
Rot[XY'Z”] =[-7.9, 44.7, 16.2]°
atau
Rot[ZY'Z”] =[7.9, 45.2, 5.0]°
atau genap
Quaternion[q1-q4] =[0.9, -0.1, 0.4, 0.1]

 Semua ini merujuk pada orientasi yang persis sama!
Yang membuatnya lebih membingungkan adalah bahwa produsen robot yang berbeda menggunakan konvensi yang berbeda. Semuanya bisa menjadi sedikit memusingkan, bahkan jika Anda sudah familiar dengan geometri 3D.

Masalahnya:Kita Tidak Berpikir Berputar

Masalah sebenarnya adalah kita tidak berpikir secara alami dalam hal rotasi.

Kami secara intuitif memahami koordinat translasi karena kami menggunakannya dalam kehidupan sehari-hari (mis. “Ada di rak kedua ke bawah, empat buku dari kiri.” ). Namun, ketika kita harus menggambarkan suatu orientasi, kita terpaksa menunjuk dengan jari kita dan mengatakan “Itu ke arah itu.”

Sayangnya, robot membutuhkan informasi yang lebih tepat daripada “itu ada di sana” yang tidak jelas.

Yang kita butuhkan adalah pemahaman yang kuat tentang Sudut Euler.

Apa itu Sudut Euler?

Mari kita mundur selangkah dan mulai dengan dasar-dasarnya.

Metode paling umum untuk mendeskripsikan orientasi robot adalah Sudut Euler. Sudut Euler terdiri dari tiga angka yang masing-masing menggambarkan rotasi di sekitar satu sumbu. Ada konvensi Sudut Euler yang berbeda tergantung pada urutan rotasi.

Pertama, mari sederhanakan ini menjadi contoh satu sumbu.

Bayangkan kompas.

Seringkali sumbu Z dunia mengacu pada sumbu yang membentang dari langit ke tanah. Jadi, Anda dapat menganggap jarum pada kompas berputar di sekitar sumbu Z (bernama Rot[Z]). Saat Anda memegang kompas di depan Anda dan panah menunjuk ke 135 °, itu berarti Utara berada di atas bahu kiri Anda sehingga Anda saat ini menghadap ke Tenggara. Tidak masalah di mana Anda menempatkan kompas (di lantai, di kepala Anda, dll) jika memiliki orientasi yang sama, sudutnya akan selalu 135 °.

Sejauh ini, sangat sederhana.

Kompas kita hanya memiliki satu nilai rotasi (yaitu Rot[Z]) tetapi untuk menggambarkan orientasi 3D kita membutuhkan tiga nilai. Di sinilah semuanya mulai menjadi sedikit lebih rumit.

Metode lain untuk mendeskripsikan orientasi robot adalah Quaternions atau Poses (matriks 4×4).

Ayo Bersiap

Mulai sekarang, akan sangat membantu jika Anda memiliki alat bantu visual interaktif.

Saya sarankan Anda mengunduh salinan RoboDK gratis di tautan ini, yang membuatnya sangat mudah untuk memvisualisasikan bingkai referensi dan melihat koordinat yang dihasilkan.

Luncurkan RoboDK dan buat bingkai referensi menggunakan tombol “Tambah Bingkai Referensi” atau pilih opsi di menu Program. Anda akan melihat bingkai merah, hijau, dan biru muncul di tengah layar.

Anda dapat memutar bingkai seperti ini:tahan tombol Alt, lalu klik dan seret salah satu panah melengkung yang muncul.

Cara Menerbangkan Pesawat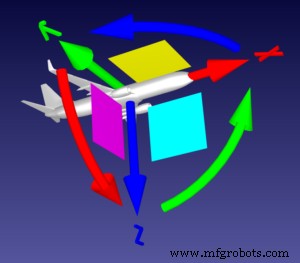

Mari kita gunakan analogi pesawat, seperti yang dijelaskan dengan sangat jelas di forum robot.

Bayangkan kerangka referensi adalah bidang. Ujung panah merah lurus (sumbu X) adalah ujung kerucut hidungnya dan panah hijau lurus (sumbu Y) adalah sayap kirinya.

Dalam hal ini, memindahkan panah melengkung memiliki fungsi berikut:

• Panah merah melengkung =Rot[X]:Gulungan pesawat, yang memungkinkan pesawat berputar pada sumbu horizontalnya.
• Panah hijau melengkung =Rot[Y]:Pitch pesawat, yang mengarahkan kerucut hidung ke atas atau ke bawah.
• Panah biru melengkung =Rot[Z]:Yaw pesawat, yang menentukan arah yang dituju pesawat.

Jika pilot ingin pesawat berbelok ke kiri dan ke bawah, secara bertahap, pesawat tidak hanya berputar pada sumbu Z — begitulah cara kerja pesawat.

Sebaliknya, pesawat akan:

1. Turunkan kerucut hidungnya:Busuk[Y]
2. Gulung pesawat ke kiri:-Rot[X]
3. Yaw ke kiri:Rot[Z]

Seluruh gerakan ini akan direpresentasikan sebagai Rot[XYZ]. Coba gerakkan sedikit bingkai di RoboDK hingga Anda merasa nyaman dengan konsep ini.

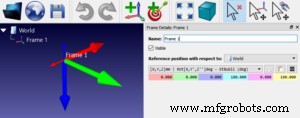
Kemudian, klik dua kali nama bingkai di kiri atas jendela utama untuk membuka panel “Rincian Bingkai”.

Satu Orientasi, Beberapa Kemungkinan Rotasi

Menggunakan RoboDK, coba tugas berikut.

Sebelum setiap tugas, setel ulang bingkai dengan membuka ikon menu "hamburger" (tiga garis horizontal) di panel Detail Bingkai dan memilih "Setel ulang (setel identitas)".

1. Pilih menu tarik-turun di atas koordinat dan pilih rotasi Stäubli (X->Y’->Z”) alih-alih Generik.
2. Putar bingkai sehingga biru (Z) mengarah ke bawah dan merah (X) mengarah ke belakang (yaitu keduanya dibalik dari posisi awal dan hijau (Y) sama dengan posisi awal), tetapi hanya lakukan jadi dengan memutar pada sumbu Y.
3. Setel ulang bingkai lalu pindahkan lagi ke putaran yang sama. Namun, kali ini hanya menggunakan satu putaran Z dan kemudian satu putaran X.
4. Setel ulang bingkai lalu pindahkan lagi ke putaran yang sama. Namun, kali ini hanya menggunakan satu putaran X dan kemudian satu putaran Z.

Seperti yang Anda lihat, ada lebih dari satu cara untuk mencapai orientasi yang sama.

Metode pertama yang bisa kita sebut Rot[Y], karena hanya mencakup rotasi terhadap sumbu Y. Metode kedua kita dapat menyebutnya Rot[Z, X’], karena ini mencakup satu putaran terhadap sumbu Z dan satu putaran terhadap sumbu X yang baru. Yang ketiga kita sebut Rot[X, Z’]. Simbol prima berarti rotasi terjadi sehubungan dengan gerakan terakhir, bukan sumbu statis.

Ini adalah konsep dasar di balik sudut Euler. Anda dapat memutar bingkai ke orientasi yang sama dalam berbagai cara dengan mengubah urutan sumbu dan rotasi.

Produsen robot yang berbeda telah memilih kombinasi rotasi yang berbeda. Misalnya, Stäubli menggunakan konvensi XY’Z”, Adept menggunakan konvensi ZY’Z”, KUKA menggunakan konvensi ZY’X” dan Fanuc &Motoman menggunakan konvensi XYZ. Di sisi lain, ABB menggunakan Quaternion dan Universal Robots menggunakan vektor orientasi. Tetapi semua konvensi dapat digunakan untuk mewakili orientasi apa pun dalam ruang.

Anda akan menemukan informasi selengkapnya di Dokumentasi RoboDK.

Uji Berbagai Konvensi Robot

Mudah-mudahan, ini mulai masuk akal. Namun, ini hanya permulaan. Untuk benar-benar menguasai konvensi sudut Euler di RoboDK, saya merasa berguna untuk bermain-main dengan perangkat lunak yang mengikuti panduan ini.

Anda dapat melihat efek rotasi angka dalam kotak biru muda, ungu, dan kuning di panel “Rincian Bingkai”.

Secara default, konvensi XYZ Generik dipilih untuk kerangka referensi baru. Coba pilih produsen robot yang berbeda dari menu tarik-turun di atas kotak berwarna. Coba masukkan nilai numerik ke dalam kotak untuk melihat efeknya pada kerangka referensi.

Untuk tutorial mendalam tentang sudut Euler, saya juga dapat merekomendasikan halaman ini di Mecademic.