bahan nano








Kami secara teoritis menyelidiki masalah elektron yang terbatas pada nanohelix antara dua gerbang paralel yang dimodelkan sebagai kabel bermuatan. Sistem nanohelix double-gated adalah superlattice biner dengan sifat yang sangat sensitif terhadap tegangan gerbang. Secara khusus, struktur pita menunjukkan persilangan pita energi untuk kombinasi tegangan gerbang tertentu, yang dapat menyebabkan fenomena seperti Dirac kuasi-relativistik. Analisis kami untuk transisi optik yang diinduksi oleh cahaya terpolarisasi linier dan sirkuler menunjukkan bahwa nanohelix berpintu ganda dapat digunakan untuk aplikasi optoelektronik serbaguna.
Dari fosil gastropoda spiral yang dikumpulkan dengan antusias oleh penulis pertama di masa kecilnya, hingga struktur DNA yang terjalin yang tidak diragukan lagi pernah mendefinisikan makhluk prasejarah itu, geometri heliks lazim di seluruh alam [1]. Terinspirasi oleh fungsionalitas kompleks yang dikaitkan dengan bentuk bio-molekul yang terjadi secara alami [2-6], diharapkan bahwa sistem lain yang memiliki geometri heliks yang cocok untuk nanoteknologi akan menghasilkan fisika yang kaya dan berkontribusi pada aplikasi baru. Selama tiga dekade terakhir, kemajuan luar biasa dalam teknik fabrikasi nano telah menyebabkan realisasi nanoheliks di sejumlah sistem yang berbeda termasuk InGaAs/GaAs [7], Si/SiGe [8], ZnO [9-11], CdS [ 12], SiO2 /SiC [13, 14], dan karbon murni [15–20], serta semikonduktor II-VI dan III-V [21] (untuk kondisi terkini lihat Referensi [21–26]). Akibatnya, sejumlah besar fenomena diharapkan dalam struktur seperti itu mulai dari sifat transportasi eksotis seperti pemompaan muatan terkuantisasi topologi [27, 28], superkonduktivitas [29], dan penyaringan putaran [30-32], hingga elektronik molekuler dan nanomekanis yang dapat diregangkan [33, 34] karena efek piezoelektrik [35], aplikasi penginderaan [36, 37], energi- [38] dan penyimpanan hidrogen [39], dan transistor efek medan [40, 41].
Daya tarik dalam perangkat berbasis nanohelix pada akhirnya berasal dari periodisitas inheren yang dikodekan dalam topologi struktur heliks. Secara khusus, menundukkan nanohelix ke medan listrik transversal (normal terhadap sumbu heliks) menimbulkan perilaku superlattice seperti hamburan Bragg elektron pada potensi super-periodik, yang mengarah ke pemisahan energi di tepi zona Brillouin superlattice antara negara bagian terendah yang dapat disetel secara linier oleh medan listrik [42, 43]. Perilaku ini dapat mengakibatkan osilasi Bloch dan konduktansi diferensial negatif [44, 45], dan dapat menekankan transportasi terpolarisasi spin melalui heliks [31, 46], serta menghasilkan peningkatan dichroism melingkar yang berguna dalam aplikasi chiroptical nanophotonic [47]. Sistem ini merupakan superlattice unary dan selanjutnya membuka kemungkinan untuk menggunakan nanoheliks baik sebagai dioda terowongan atau dioda Gunn untuk mengalikan frekuensi, amplifikasi, dan generasi atau penyerapan radiasi dalam kisaran terahertz yang dipuji [48-51]. Sementara superlattice prototipe biasanya diwujudkan dalam heterostruktur lapisan semikonduktor bolak-balik dengan celah pita intrinsik yang berbeda, parameter superlattice nanohelix sepenuhnya dikendalikan oleh medan eksternal. Sebaliknya, bentuk potensi superlattice konvensional sebelumnya khusus untuk heterostruktur dan, meskipun kuat, menawarkan kemampuan terbatas untuk manipulasi selama eksploitasinya tanpa menggunakan medan eksternal yang besar. Oleh karena itu, daya tarik dalam menggunakan nanoheliks sebagai superlattice sebagai penggantinya terletak pada tunabilitasnya yang lebih besar.
Di sisi lain, dengan superlattice semikonduktor heterostruktur (atau bahkan struktur superlattice fotonik [52-55] dan atom dingin dalam kisi optik [56, 57]) seseorang dapat membuat sel unit superlattice yang lebih rumit di luar sumur kuantum sederhana yang diinduksi oleh medan listrik sepanjang heliks. Bahkan perluasan ke superlattice biner [58-60] (di mana sel satuan dibedakan oleh dua sumur kuantum dan/atau penghalang yang berbeda) menjanjikan susunan fisika yang kaya seperti osilasi Bloch-Zener [61], yang pada gilirannya dapat berkontribusi untuk aplikasi beam splitter dan interferometer yang dapat disetel [62]. Oleh karena itu, sangat diinginkan untuk menggabungkan tunabilitas medan eksternal dari superlattice berbasis nanohelix dengan fungsionalitas superior dari superlattice biner.
Berikut ini, kami menggambarkan sistem seperti itu, dengan nanohelix yang diposisikan di antara dua kabel bermuatan paralel yang disejajarkan dengan sumbu heliks. Kami membayangkan penerapan medan listrik transversal tambahan dan secara teoritis menunjukkan bahwa potensial yang dapat dikontrol gerbang dan medan membentuk superlattice biner di sepanjang heliks satu dimensi.
Mari kita mulai dengan mempelajari kasus nanohelix melingkar semikonduktor elektron tunggal dengan N belokan radius R , nada p , dan panjang total L =Np . Struktur nano diposisikan di antara dua gerbang paralel yang dimodelkan sebagai kabel bermuatan dengan sumbu heliksnya disejajarkan di sepanjang z -sumbu dan dengan sumbu dan gerbang semua berada pada bidang yang sama seperti yang digambarkan pada Gambar. 1. Selain itu, kami menganggap medan listrik transversal eksternal normal ke bidang sumbu gerbang \(\mathbf {E}=E_{\bot } \ topi {\mathbf {y}}\) yang dapat digunakan untuk mematahkan simetri refleksi potensial di atas bidang terhadap potensial di bawah bidang. Kami bekerja dalam koordinat heliks yang dijelaskan secara parametrik melalui r =(x,y ,z )=(R cos(s φ ),R dosa(s φ ),ρ φ ), di mana koordinat sudut dinamis φ =z /ρ hanya bergantung pada jarak sepanjang sumbu heliks dengan ρ =p /2π , dan s =±1 menunjukkan heliks tangan kiri atau kanan, masing-masing. Dalam karya ini, kami mempertimbangkan heliks tangan kiri s =1. Dalam kerangka model massa efektif, spektrum energi ε ν dari ν keadaan eigen elektron dalam heliks di bawah pengaruh potensial eksternal tersebut ditemukan dari persamaan Schrödinger:
$$ -\thinspace \frac{\hbar^{2}}{2M^{*}\rho^{2}}\frac{d^{2}}{d\varphi^{2}}\psi_{\ nu} +\left[V_{g} (\varphi) + V_{\bot} (\varphi) \right]\psi_{\nu} =\varepsilon_{\nu} \psi_{\nu} $$ (1 )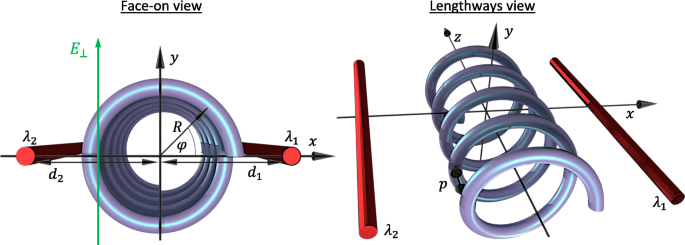
Diagram geometri dan parameter sistem dari perspektif muka dan memanjang. R adalah radius heliks, dan d 1 dan d 2 adalah jarak kabel bermuatan dari sumbu heliks dengan rapat muatan λ 1 dan λ 2 , masing-masing. Koordinat spasial φ menggambarkan posisi sudut pada heliks dari muka dan terkait dengan z -koordinasikan melalui φ =2π z /p dengan p nada helix. Medan listrik transversal E ⊥ diterapkan sejajar dengan y -sumbu
di mana kita telah menormalkan ulang massa efektif elektron secara geometris M e untuk M ∗ =M e (1+R 2 /ρ 2 ) untuk menyatakan segala sesuatu dalam bentuk koordinat sepanjang sumbu heliks (ingat bahwa φ =z /ρ ) yang lebih nyaman untuk potensi eksternal. Di sini, V ⊥ (φ )=−eE ⊥ R dosa(φ ) adalah kontribusi dari medan listrik transversal yang diarahkan sepanjang y -sumbu sedemikian rupa sehingga V ⊥ (π /2)<0. Potensi dari gerbang adalah V g (φ )=−e [Φ 1 (φ )+Φ 2 (φ )] dengan potensial elektrostatik yang dirasakan oleh elektron di sepanjang heliks karena kawat bermuatan individu yang diberikan oleh Φ i (φ )=−λ i k ln(r i /d i ). Di sini, i =1,2 memberi label pada kabel, λ i adalah kerapatan muatan linier pada kawat, dan \(k =1/2\pi \tilde {\epsilon }\) dengan \(\tilde {\epsilon }\) permitivitas mutlak. Jarak tegak lurus muatan uji dari kawat tertentu diberikan oleh \(r_{i}=[d^{2}_{i}+R^{2} + 2(-1)^{i}d_{i }R\cos (\varphi)]^{1/2}\), dengan d i menunjukkan jarak yang sesuai dari kawat ke sumbu heliks. Kami telah mendefinisikan potensi yang diinduksi gerbang nol berada di sepanjang sumbu heliks. Potensi satu dimensi total V T (φ )=V g (φ )+V ⊥ (φ ) jelas periodik V T (φ )=V T (φ +2π n ) dengan periode 2π secara umum (yang sesuai dengan periode p sehubungan dengan koordinat z ). Periode ini secara signifikan lebih besar dari jarak antar atom dan menimbulkan efek superlattice yang khas. Huruf ini berbeda dari nanohelix dalam medan listrik transversal (yang dapat direproduksi dengan V T (φ )=V ⊥ (φ ) di sini) terutama dengan memanipulasi sel satuan berulang dari superlattice melalui potensial gerbang ganda V g (φ ). Mengambil batas p →0, kita kembali ke partikel pada gambar cincin yang tunduk pada dua gerbang elektrostatik [63, 64]. Membuat pendekatan R /d i 1, kami dapat memperluas V g (φ ) sampai urutan kedua cos(φ ), dan setelah mengubah Persamaan. 1 menjadi bentuk tak berdimensi kita sampai di
$$ {\begin{aligned} \frac{d^{2} \psi_{\nu}}{d\varphi^{2}}+\left[\epsilon_{\nu} + 2A_{g}\cos( \varphi) + 2B_{g}\cos(2\varphi) + 2C_{\bot} \sin(\varphi) \right]\psi_{\nu} =0, \end{aligned}} $$ (2)dengan besaran dalam satuan skala energi \(\varepsilon _{0}(\rho) =\hbar ^{2} / 2 M^{*} \rho ^{2}\) didefinisikan sebagai
$$\begin{array}{@{}rcl@{}} A_{g} &=&\beta\frac{\left(d_{1}^{2} +R^{2}\right)}{ d_{1} R}(1-\gamma), \qquad B_{g} =\frac{\beta}{2}\left(1+\frac{\lambda_{1}}{\lambda_{2}} \gamma^{2}\right), \\ C_{\bot} &=&e E_{\bot} R /2\varepsilon_{0}(\rho), \qquad \qquad \qquad \; \epsilon_{\nu} =\frac{\varepsilon_{\nu}}{\varepsilon_{0}(\rho)}. \end{array} $$ (3)Di sini, \(\beta =ek d_{1}^{2} R^{2} \lambda _{1} /2\left (d_{1}^{2} +R^{2}\right)^ {2}\varepsilon _{0}(\rho) \) mencirikan kontribusi dari gerbang 1 sedangkan parameter asimetri \(\gamma =\lambda _{2} d_{2} \left (d_{1}^{2 } +R^{2}\right)/\lambda _{1} d_{1} \left (d_{2}^{2} + R^{2}\right)\) mencirikan kontribusi relatif dari gerbang 2 , dengan γ =1 sesuai dengan kontribusi gerbang yang sama dengan potensi (menghasilkan A g =0). Perlu dicatat bahwa asimetri yang tak terhindarkan disebabkan oleh kesulitan dalam mempertahankan d 1 =d 2 dapat dikompensasikan dengan memanipulasi λ 1 dan λ 2 . Dalam surat ini, kami membatasi diri untuk mempertimbangkan γ 1 (yaitu |Φ 1 |>|Φ 2 |) sebagai parameter asimetri yang lebih besar dari satu dapat dipetakan ke sistem setara di bawah satu melalui pertukaran sederhana dari indeks pelabelan gerbang dan pergeseran yang sesuai dalam perspektif φ →φ ±π . Kami juga hanya akan mempertimbangkan C ⊥ 0 karena simetri negatif C ⊥ sehubungan dengan terjemahan koordinat seperti di φ , dan A g 0, B g >0 (yaitu hanya rapat muatan positif pada kabel β>0) karena setiap lanskap potensial dengan gerbang bermuatan negatif dapat direproduksi dengan kombinasi parameter yang benar dari gerbang bermuatan positif. Pada Gambar 2, kami memplot potensial tak berdimensi V T (φ )/ε 0 (ρ ), dengan kekuatan π -komponen potensial periodik ditetapkan pada B g =0.2, untuk beberapa kombinasi parameter gangguan periode dua kali lipat A g dan C ⊥ . Kita melihat bahwa total potensial eksternal menginduksi superlattice biner sepanjang φ , dengan sumur kuantum ganda (DQW) sebagai sel satuan yang disorot dengan warna biru. Ini dapat mengambil bentuk yang berbeda secara kualitatif dengan memanipulasi kontribusi gerbang relatif γ dan medan listrik transversal E ⊥ . Sel satuan pada dasarnya adalah sumur tunggal di bawah kontribusi gerbang yang setara (γ =1) dan tidak ada medan listrik transversal E ⊥ =0 (seperti pada Gambar 2a untuk A g =C ⊥ =0). Memperbaiki E ⊥ =0, dengan kontribusi gerbang 1 yang lebih kuat (γ <1), sel satuan menjadi DQW dengan well minima dan degenerate barrier maxima yang berbeda (Gbr. 2b di mana A g =0.1 dan C ⊥ =0). Sebaliknya, menjaga agar DQW minima mengalami degenerasi dan memanipulasi dua hambatan potensial terhadap satu sama lain membutuhkan kontribusi gerbang simetris (γ =1) dalam medan listrik bukan nol E ⊥ 0 (Gbr. 2c dengan A g =0 dan C ⊥ =0,1). Menggabungkan kontribusi gerbang asimetris (γ <1) dengan E ⊥ 0 menghasilkan DQW dengan potensi sumur minimum yang berbeda dan hambatan yang berbeda (seperti yang terlihat pada Gambar. 2d di mana keduanya A g =C ⊥ =0,1). Ini mengarah pada perilaku yang berbeda dan kaya secara kualitatif seperti yang akan kita lihat di bagian berikut.
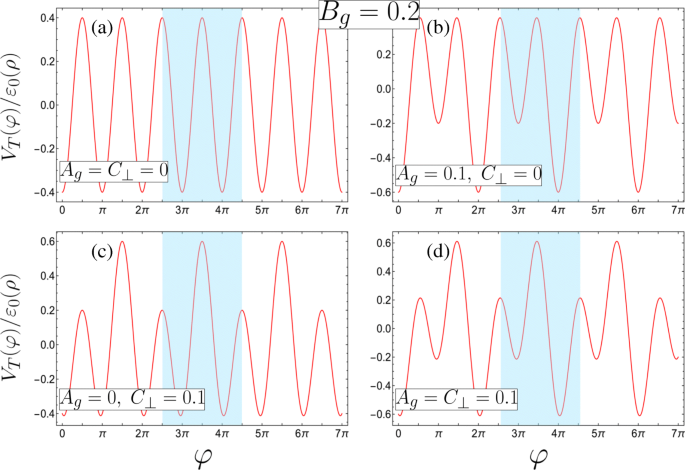
Empat kemungkinan konfigurasi potensial superlattice dengan sel satuan disorot dengan warna biru (didefinisikan dalam parameter tak berdimensi, lihat Persamaan 3 untuk persyaratan parameter fisik yang sesuai, dan semuanya dengan B g =0.2). a Sebuah superlattice unary dengan degenerasi minima dan maxima dalam sel satuan (A g =C ⊥ =0). b –d Superlattices biner terbentuk dari salah satu b DQW asimetris dengan minimum yang berbeda dan simetri refleksi internal tentang salah satu minimum karena degenerasi maxima (A g =0.1, C ⊥ =0), c DQW simetris dengan minima yang merosot saja (A g =0, C ⊥ =0.1), atau d DQW asimetris dengan minimum dan maksimum yang berbeda (A g =C ⊥ =0.1)
Solusi untuk Persamaan. 2 dapat ditemukan dalam hal fungsi Bloch
$$ \psi_{n,q}(\varphi)=(2\pi N \rho)^{-\frac{1}{2}}e^{iq \varphi}\sum_{m} c^{( n)}_{m,q} e^{im \varphi}, $$ (4)di mana q =k z ρ adalah bentuk tak berdimensi dari kuasimomentum elektron k z sepanjang sumbu heliks, n menunjukkan subband, dan prefactor muncul dari normalisasi dalam hal φ :\(\rho \int _{0}^{2\pi N}|\psi _{n,q}(\varphi)|^{2} d\varphi =1\). Kami menggunakan ortogonalitas fungsi eksponensial dengan mengalikan ekspresi yang dihasilkan dengan \(e^{im^{\prime } \varphi }/2\pi \) dan integrasikan dengan φ , di mana m ′ adalah bilangan bulat, sehingga kita sampai pada himpunan tak hingga persamaan simultan untuk koefisien \(c^{(n)}_{m,q}\),
$$ {\begin{aligned} &\left[(q+m)^{2}-\epsilon_{n}\right]c^{(n)}_{m} - \left(A_{g} - i C_{\bot} \right)c^{(n)}_{m-1} - \left(A_{g} + i C_{\bot} \right)c^{(n)}_{m +1}\\ &\quad- B_{g}\left(c^{(n)}_{m+2}+c^{(n)}_{m-2} \right)=0, \ akhir{selaras}} $$ (5)di mana untuk kejelasan q -notasi subskrip telah dihapus, ε n,q ε n dan \(c_{m}^{(n)}\equiv c_{m,q}^{(n)} \). Persamaan 5 merupakan matriks penta-diagonal tak terbatas dimana jelas bahwa sistem periodik di q , dan kami dapat membatasi pertimbangan kami pada zona Brillouin pertama yang ditentukan oleh 1/2≤q 1/2. Dengan tidak adanya potensi superlattice A g =B g =C ⊥ =0, nilai eigen kemudian dihitung dengan m diberikan oleh ε m =(m +q ) 2 dan kami mengenali m menjadi bilangan kuantum momentum sudut yang terkait dengan elektron bebas pada heliks. Kita lihat dari Persamaan. 5 bahwa ketika A g =C ⊥ =0 hanya negara bagian dengan Δ m =±2 dicampur, sedangkan pembentukan sel unit DQW dengan minima atau hambatan sumur yang berbeda, dicapai melalui A g 0 dan/atau C ⊥ 0, juga mencampur status dengan Δ m =± 1. Menariknya, sistem elektron pada heliks di bawah potensial transversal eksternal (yang bervariasi di satu putaran heliks) secara matematis setara dengan elektron pada cincin kuantum yang ditembus oleh medan magnet dan tunduk pada potensial dengan bentuk fungsional yang sama bervariasi sepanjang koordinat sudut; misalnya lihat Ref. [65–67] atau bandingkan misalnya Ref. [42-45] dengan [68-70]. Untuk sebuah cincin, peran yang dimainkan oleh q di sini diambil oleh fluks magnet. Oleh karena itu, analisis yang persis sama dalam karya ini berlaku untuk masalah cincin kuantum gerbang ganda [63–66], jika cincin itu ditembus oleh fluks magnet.
Memotong dan mendiagonalisasi secara numerik matriks yang sesuai dengan Persamaan. 5 menyediakan n energi eigen subband ε n dan koefisien \(c_{m}^{(n)}\) untuk setiap nilai q . Kami menerapkan pemotongan di |m |=10, aman karena mengetahui bahwa setiap peningkatan ukuran matriks tidak menghasilkan perubahan yang berarti pada subband terendah.
Kami memplot pada Gambar. 3 dispersi energi pita terendah untuk beberapa kombinasi parameter. Tergantung pada bentuk superlattice kami menemukan variasi yang luar biasa dalam perilaku dispersi, dan untuk beberapa kombinasi parameter tertentu kami menemukan persilangan pita energi untuk subband tertentu baik di tepi zona Brillouin (Gbr. 3a dan c) atau di pusat zona Brillouin (Gbr. 3b dan d).
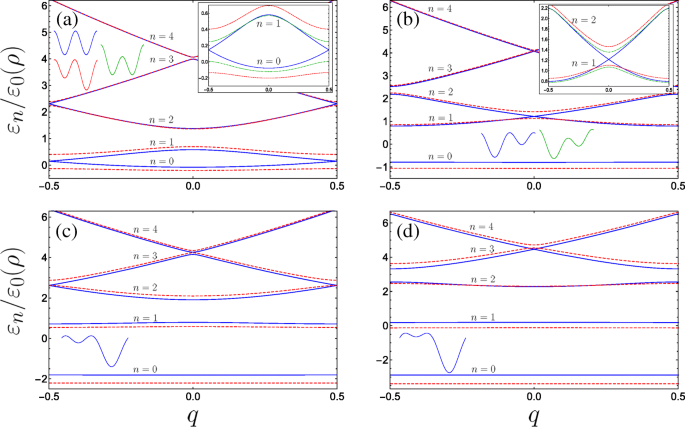
Struktur pita untuk sistem nanohelix gerbang ganda untuk berbagai kombinasi parameter tak berdimensi (dengan B g =0,4 tetap di seluruh):a Plot biru solid (merah putus-putus) A g =0 &C ⊥ =0 (A g =0.2 &C ⊥ =0), inset juga memplot perilaku dua subband terbawah yang dikenai medan listrik transversal dengan A g =0 &C ⊥ =0.2 sebagai kurva hijau putus-putus titik. b Plot biru solid (merah putus-putus) A g =0,63 &C ⊥ =0 (A g =0,8 &C ⊥ =0) di mana kurva biru menggambarkan kejadian pertama resonansi (lihat teks) dengan pita energi bersilangan di pusat zona Brillouin, inset membandingkan perilaku dua subband tereksitasi bawah dengan kasus di mana A g =0,63 &C ⊥ =0.2 sebagai kurva titik-titik hijau. c Plot biru solid (merah putus-putus) A g =1,26 &C ⊥ =0 (A g =1.5 &C ⊥ =0) di mana kurva biru menggambarkan kejadian kedua resonansi dengan celah energi menutup di tepi Brillouin untuk pita yang lebih tinggi. d Resonansi ketiga dan minigap subband yang lebih tinggi menutup di tengah, dengan warna biru solid (merah putus-putus) menjadi A g =1.9 &C ⊥ =0 (A g =2.2 &C ⊥ =0). Bentuk sel satuan dibuat sketsa, n menghitung pita, dan sumbu sisipan sama dengan grafik utama
Ketika A g =C ⊥ =0, sel satuan merupakan dua sumur kuantum yang setara, dan akibatnya munculnya pasangan pita yang bersentuhan di tepi zona Brillouin muncul secara alami. Memang, mengambil hanya satu sumur sebagai sel satuan membagi dua periode superlattice dan menghasilkan penggandaan zona Brillouin − 1≤q 1. Kami kemudian akan mengamati diagram pita superlattice unary biasa, di mana celah pita antara ground dan pita pertama di q =1 diberikan di sini melalui celah pita antara n =1 dan n =2 di q =0 dan akan linier dalam B g dari teori gangguan. Namun, kami menyajikan deskripsi struktur pita di |q |=1/2 pada gambar sel satuan DQW menggunakan aljabar matriks pada Lampiran. Seperti terlihat pada sisipan Gambar 3a, pengenalan salah satu dari istilah potensial periode ganda membuka celah pita di tepi zona Brillouin. Sel satuan dari kontribusi gerbang simetris (A g =0) mempertahankan bentuk DQW simetris di bawah penerapan medan transversal C ⊥ tegak lurus terhadap sumbu gerbang heliks, dengan satu penghalang potensial dimodifikasi sehubungan dengan yang lain (ditunjukkan oleh sketsa DQW hijau pada Gambar. 3a). Sementara C ⊥ membuka celah pita, modifikasi dispersi terutama kurang sensitif dibandingkan dengan modifikasi dari besaran yang sama dari penerapan A g . Hal ini terlihat dari celah pita yang lebih kecil pada |q |=1/2 untuk garis hijau putus-putus di sisipan Gambar 3a (dengan A g =0 dan C ⊥ =0,2) dibandingkan dengan celah yang lebih besar untuk kurva merah putus-putus (yaitu untuk A g =0.2 dan C ⊥ =0). Untuk menekankan perilaku ini, Gambar 4a memplot ukuran celah energi di |q |=1/2 antara dua subband terendah \(\Delta \varepsilon _{01}^{(q=1/2)}/\varepsilon _{0}(\rho)\) untuk B
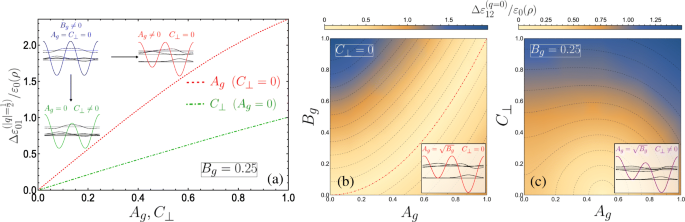
a Ukuran celah pita antara ground dan subband pertama sebagai fungsi A g (C ⊥ ) diplot sebagai merah putus-putus (hijau putus-putus), di sini B g =0,25. Diagram menunjukkan pengaruh gangguan yang berbeda pada sel unit DQW yang terisolasi dan status eigen. b –c Ukuran celah pita antara subband pertama dan kedua ditunjukkan melalui plot kepadatan 2D sebagai fungsi dari; b A g dan B g untuk C ⊥ =0, dan c A g dan C ⊥ dengan B . tetap g =0,25. b Garis kontur isoenergi yang berdekatan menunjukkan perbedaan 0,17, dengan celah nol diberikan oleh garis merah putus-putus untuk \(A_{g}=\sqrt {B_{g}}\), sedangkan c selisihnya 0,13 dengan celah nol di tengah kontur setengah lingkaran terkecil (0,5,0). Diagram membuat sketsa DQW dan keadaan eigen yang terisolasi. Hibridisasi tidak terjadi antara s -suka dan p -seperti keadaan sumur individu yang terlokalisasi resonansi di b , tetapi tidak di c karena medan listrik mengubah satu penghalang terhadap yang lain
Sangat luar biasa untuk melihat bahwa jika kita tetap C ⊥ =0 dan tingkatkan A g , sementara awalnya semua degenerasi diangkat, pita energi yang lebih tinggi berikutnya dibawa untuk saling bersilangan bergantian antara pusat dan tepi zona Brillouin (amati perilaku bergantian kurva biru dan merah putus-putus yang berkembang dari Gambar 3a hingga d). Secara fisik, kita dapat memahami celah pita hilang dalam hal interaksi fungsi gelombang terlokalisasi dalam sel satuan. Ketika potensial DQW asimetris sedemikian rupa sehingga keadaan dasar di sumur dangkal (s -seperti orbital) beresonansi dengan keadaan tereksitasi pertama di sumur yang lebih dalam (p -seperti orbital), di q =0 karena simetri refleksi tentang pusat salah satu sumur, paritas yang berlawanan dari keadaan ini mencegah kopling terowongan yang biasa di antara mereka, dan akibatnya keadaan tereksitasi yang dibangun dari orbital ini bertepatan (kurva biru pada Gambar 3b). Ini mengingatkan pada apa yang disebut s p resonansi dalam kisi optik [73, 74]. Dengan cara yang sama, jika parameternya sedemikian rupa sehingga keadaan dasar terlokalisasi di sumur dangkal beresonansi dengan keadaan tereksitasi di sumur yang lebih dalam yang memiliki paritas yang sama, maka pada |q |=1/2, kehadiran fase Bloch sepenuhnya menekan hibridisasi biasa antara dua keadaan sumur lokal yang berdekatan ini dan celah pita ditutup (seperti yang ditunjukkan pada Gambar 3c untuk resonansi tanah dengan keadaan tereksitasi kedua). Dalam bahasa hamburan dari potensi periodik; celah pita ditutup karena interferensi destruktif lengkap dari amplitudo hamburan Bragg orde kedua dari cos(φ ) amplitudo hamburan potensial dan orde pertama dari cos(2φ ) potensi [75–77].
Kita dapat secara kuantitatif menunjukkan adanya persilangan pita energi (untuk medan listrik transversal nol) di pusat dan tepi zona Brillouin dengan kembali ke Persamaan. 2, yang dapat dikenali sebagai persamaan Whittaker-Hill ketika C ⊥ =0 [78]. Fungsi Bloch Persamaan. 4 mematuhi kondisi batas periodik yang bengkok ψ n,q (φ +2π )=exp(2π iq )ψ n,q (φ ). Khususnya, ketika q =0 solusi formal untuk Persamaan. 2 adalah 2π -berkala, sedangkan kapan |q |=1/2 solusi adalah 2π -antiperiodik (dan karena itu kita akan mencari 4π -solusi periodik). Secara khusus, Persamaan. 2 dengan C ⊥ =0 dapat dipetakan ke persamaan Ince [79, 80], yang dapat dipecahkan secara kuasi-persis, melalui ekspresi fungsi gelombang sebagai produk dari solusi asimtotik ke Persamaan. 2 dan fungsi yang tidak diketahui \(\psi _{n,q}(\varphi) =\exp \left [ -2\sqrt {B_{g}}\cos (\varphi)\right ]\Phi _{n, q}(\varphi)\), sehingga
$$ \frac{d^{2} \Phi_{n,q}}{d \varphi^{2}} + \frac{\xi}{2} \sin(\varphi)\frac{d\Phi_{ n,q}}{d\varphi} +\frac{1}{4}\left[ \eta_{n,q} - p\xi\cos(\varphi) \right]\Phi_{n,q} =0, $$ (6)di mana kita telah mendefinisikan parameter bantu \(\xi =8\sqrt {B_{g}}\), η n,q =4ε n,q +8B g , \(-p \xi =8A_{g}+8\sqrt {B_{g}}\), dan Φ n,q (φ ) mempertahankan periodisitas bengkok yang diperlukan dari setiap solusi (perhatikan bahwa di sini p adalah tidak nada heliks). Selain itu, karena potensi superlattice di sini adalah invarian di bawah transformasi φ →− φ , solusi untuk q =0 dan q =1/2 dapat dipisahkan menjadi paritas ganjil dan genap, sehingga deret trigonometri berikut
$$ \Phi_{n,0}^{(e)}(\varphi) =\sum_{l=0}a^{(n)}_{l}\cos(l\varphi), $$ (7a ) $$ \Phi_{n,0}^{(o)}(\varphi) =\sum_{l=0}b^{(n)}_{l+1}\sin[(l+1)\ varphi], $$ (7b) $$ \Phi_{n,\frac{1}{2}}^{(e)}(\varphi) =\sum_{l=0}\widetilde{a}^{( n)}_{l}\cos\left[\left(l+\frac{1}{2}\right)\varphi\right], $$ (7c) $$ \Phi_{n,\frac{1} {2}}^{(o)}(\varphi) =\sum_{l=0}\widetilde{b}^{(n)}_{l+1}\sin\left[\left(l+\frac {1}{2}\kanan)\varphi\kanan], $$ (7d)mencakup solusi formal, dan kami mencatat bahwa solusi untuk q =−1/2 sama dengan q =1/2. Di sini, superskrip e dan o beri label masing-masing fungsi sebagai genap dan ganjil, dan n masih mengacu pada n subband th, yang juga merupakan n eigenstate untuk q yang ditentukan ini nilai-nilai. Substitusi ini ke dalam Persamaan. 6 menghasilkan hubungan rekursi tiga suku untuk koefisien fourier. q =0 solusi genap menghasilkan
$$ -\eta_{n,0}^{(e)}a^{(n)}_{0} + \xi\left(\frac{p}{2} +1 \right) a^{( n)}_{2} =0, $$ (8a) $$ \xi pa^{(n)}_{0} + \left(4 - \eta_{n,0}^{(e)} \ kanan)a^{(n)}_{2} + \xi \left(\frac{p}{2} +2 \right)a^{(n)}_{4}=0, $$ (8b ) $$ {\begin{aligned} &\xi \left(\frac{p}{2} - l +1 \right)a^{(n)}_{2l-2} + \left(4l^{ 2} - \eta_{n,0}^{(e)} \kanan)a^{(n)}_{2l}\\ &\quad+\xi \left(\frac{p}{2} + l +1 \right)a^{(n)}_{2l+2} =0, \qquad (l \ge 2) \end{aligned}} $$ (8c)dan hubungan rekursi yang sesuai untuk solusi ganjil untuk q =0 adalah
$$ (4 - \eta_{n,0}^{(o)})b^{(n)}_{2} + \xi \left(\frac{p}{2} +2 \right)b ^{(n)}_{4} =0, $$ (9a) $$ {\begin{aligned} &\xi \left(\frac{p}{2} - l +1 \right)b^{ (n)}_{2l-2} + \left(4l^{2} - \eta_{n,0}^{(o)} \kanan)b^{(n)}_{2l} +\xi \left(\frac{p}{2} + l +1 \right)b^{(n)}_{2l+2}\\ &=0. \qquad (l \ge 2) \end{aligned} } $$ (9b)The q =1/2 even solution gives
$$ \left[ 1 -\eta_{n,\frac{1}{2}}^{(e)} +\frac{\xi}{2}(p+1) \right]\widetilde{a}^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{a}^{(n)}_{3}=0, $$ (10a) $$ {}{\begin{aligned} &\frac{\xi}{2}(p-2l +1)\widetilde{a}^{(n)}_{2l-1}+\left[(2l+1)^{2} - \eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{a}^{(n)}_{2l+1}\\ &\quad+ \frac{\xi}{2}(p+2l+3)\widetilde{a}^{(n)}_{2l+3}=0, \qquad (l \ge 1) \end{aligned}} $$ (10b)and the q =1/2 odd solution gives
$$ \left[ 1 -\eta_{n,\frac{1}{2}}^{(e)} -\frac{\xi}{2}(p+1) \right]\widetilde{b}^{(n)}_{1} +\frac{\xi}{2}(p+3)\widetilde{b}^{(n)}_{3}=0 $$ (11a) $$ {}{\begin{aligned} &\frac{\xi}{2}(p-2l+1)\widetilde{b}^{(n)}_{2l-1}+\left[(2l+1)^{2} -\eta_{n,\frac{1}{2}}^{(e)}\right]\widetilde{b}^{(n)}_{2l+1}\\&\quad + \frac{\xi}{2}(p+2l+3)\widetilde{b}^{(n)}_{2l+3}=0. \qquad (l \ge 1) \end{aligned}} $$ (11b)Consider then Eqs. (8c) and (9b) for the q =0 solutions. The series solutions (7a) and (7b) can clearly be made to terminate if p is 0 or an even positive integer. The resulting polynomials are referred to as Ince polynomials. The remaining solutions for higher eigenvalues are simultaneously double degenerate and correspond to the energy crossings observed at q =0 for certain parameters. The existence of these degeneracies can be seen by looking at the diagonalizable matrices describing the recursion relations for a l dan b l :
$$ \boldsymbol{\mathcal{A}} =\left[ \begin{array}{ccccc} 0 &\xi\left(\frac{p}{2} +1 \right) &0 &0 &\hdots \\ \xi p &4 &\xi\left(\frac{p}{2} +2 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \end{array} \right]\!, $$ (12)dan
$$ \boldsymbol{\mathcal{B}} =\left[ \begin{array}{ccccc} 4 &\xi\left(\frac{p}{2} +2 \right) &0 &0 &\hdots \\ \xi\left(\frac{p}{2} - 1 \right) &16 &\xi\left(\frac{p}{2} +3 \right) &0 &\hdots \\ 0 &\xi\left(\frac{p}{2} -2 \right) &36 &\xi\left(\frac{p}{2} +4 \right) &\hdots \\ \vdots &\vdots &\vdots &\vdots &\ddots \\ \end{array} \right]\! $$ (13)masing-masing. Either of the above tridiagonal matrices can be broken into tridiagonal sub-matrices if a leading off-diagonal matrix element is equal to zero, i.e. if p is an even number. The matrices will decompose into two tridiagonal blocks, one smaller finite matrix \(\boldsymbol {\mathcal {A}_{1}}\) (\(\boldsymbol {\mathcal {B}_{1}}\)) and a remaining infinite matrix \(\boldsymbol {\mathcal {A}_{2}}\) (\(\boldsymbol {\mathcal {B}_{2}}\)). From the theory of tridiagonal matrices the corresponding eigenvalue spectra for each matrix is then \(\eta (\boldsymbol {\mathcal {A}}) =\eta (\boldsymbol {\mathcal {A}_{1}}) \cup \eta (\boldsymbol {\mathcal {A}_{2}})\) and \(\eta (\boldsymbol {\mathcal {B}}) =\eta (\boldsymbol {\mathcal {B}_{1}}) \cup \eta (\boldsymbol {\mathcal {B}_{2}})\). The smaller finite matrices are analytically diagonalizable in principle, giving exact eigenvalues, and their corresponding finite length eigenvectors define the fourier coefficients yielding Ince polynomials via Eq. 7. We can see that for a given even integer p , the remaining infinite tridiagonal matrices are the same \(\boldsymbol {\mathcal {A}_{2}}=\boldsymbol {\mathcal {B}_{2}}\equiv \boldsymbol {\mathcal {D}}\) which results in the double degenerate eigenvalues. To be clear, we provide an example of when p =2 in the Appendix.
In the same way, when p is a positive odd integer the series solutions (7c) and (7d) can be made to terminate, and the matrices corresponding to \(\widetilde {a}_{l}\) and \(\widetilde {b}_{l}\) share eigenvalues resulting in the closing of higher subbands at the edge of the Brillouin zone q =± 1/2. From the definitions of the auxiliary parameters in Eq. 6, we have
$$ A_{g} =(p+1)\sqrt{B_{g}}, $$ (14)which defines the condition for exactly-solvable solutions for the lower lying solutions and simultaneously the existence of higher double degenerate eigenvalues above the p th subband, with p =0 or an even positive integer corresponding to crossings at the centre of the Brillouin zone, while crossings at the edge require p to be an odd positive integer. Figure 4b plots the size of the band gap between the first and second subbands \(\Delta \varepsilon _{12}^{(q=0)}/\varepsilon _{0}(\rho)\) as a function of A g dan B g , with the dot-dashed red contour line corresponding to Eq. 14 for p =0. The schematic indicates the appropriate eigenstates of the isolated DQW at the p =0 resonance.
The application of a small transverse field C ⊥ breaks the reflection symmetry of the system, permitting hybridization of the localized well states of the isolated DQW which results in a significant change at points of degeneracy, as can be seen by comparing the schematic depicted in Fig. 4b with that in c (see also inset of Fig. 3b). We plot in Fig. 4c the behaviour of the band gap between the first and second subbands as a function of A g dan C ⊥ . Here we see that the band gap is more sensitive to C ⊥ due to the significant change in the isolated DQW eigenstates by lowering one barrier with respect to the other. This behaviour is notably the converse of the parameter sensitivity for the band gap between the ground and first subbands. By degenerate perturbation theory, it can be shown that this induced band gap is linear in C ⊥ for the lowest crossing bands when p =0, and to higher order with increasing p . Finally, within the vicinity of the crossings, e.g. for small q about q =0 in Fig. 3a, the dispersions could be approximated as a quasi-relativistic linear dispersion yielding Dirac-like physics, which could permit superfluiditiy [81] for example. The advantage in using nanohelices lies in introducing such phenomena to portable nanostructure based devices, while also exhibiting unusual responses of the charge carriers to circularly polarized radiation [44, 45, 82–85] (or indeed magnetic fields [86, 87]) due to the helical spatial confinement.
In order to understand how our double-gated nanohelix system interacts with electromagnetic radiation, we study the inter-subband momentum operator matrix element \(T^{g\rightarrow f}_{j} =\langle {f}|\boldsymbol {\hat {j}} \cdot \boldsymbol {\hat {P}}_{j} |{g}\), which is proportional to the corresponding transition dipole moment, and dictates the transition rate between subbands ψ f and ψ g . Here, \(\boldsymbol {\hat {j}}\) is the projection of the radiation polarization vector onto the coordinate axes (j =x,y ,z ) and the respective self-adjoint momentum operators are [44, 45, 82–84]
$$ \boldsymbol{\hat{P}}_{x} =\boldsymbol{\hat{x}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\sin(\varphi)\frac{d}{d\varphi} + \frac{1}{2}\cos(\varphi) \right], $$ (15a) $$ \boldsymbol{\hat{P}}_{y}=-\boldsymbol{\hat{y}}\frac{i \hbar R}{\rho^{2} +R^{2}}\left[\cos(\varphi)\frac{d}{d\varphi} - \frac{1}{2}\sin(\varphi) \right], $$ (15b) $$ \boldsymbol{\hat{P}}_{z}=-\boldsymbol{\hat{z}}\frac{i \hbar \rho}{\rho^{2} +R^{2}}\frac{d}{d\varphi}. $$ (15c)In terms of the dimensionless position variable φ , we are required to evaluate \(T^{g\rightarrow f}_{j} =\rho \int _{0}^{2\pi N}\psi _{f}^{\ast } P_{j} \psi _{g} d\varphi \), and upon substituting in from Eq. 4 we find
$$ {\begin{aligned} T^{g\rightarrow f}_{x} &=\frac{i \hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\ &\quad\left.-c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16a) $$ {\begin{aligned} T^{g\rightarrow f}_{y} &=\frac{\hbar R}{2\left(\rho^{2} + R^{2} \right)}\sum_{m} c_{m}^{\ast (f)} \left[ c_{m-1}^{(g)} \left(q+m-\frac{1}{2}\right)\right.\\&\left.\quad+c_{m+1}^{(g)} \left(q+m+\frac{1}{2}\right) \right], \end{aligned}} $$ (16b) $$ T^{g\rightarrow f}_{z} =\frac{\hbar \rho}{\left(\rho^{2} + R^{2} \right)} \sum_{m} c_{m}^{\ast (f)} c_{m}^{(g)} (q+m). $$ (16c)We see from Eqs. 16a and 16b that light linearly polarized transverse to the helix axis couples coefficients with angular momentum differing by unity Δ m =± 1, whereas from Eq. 16c, linear polarization parallel to the helix axis couples only Δ m =0. In Fig. 5, we plot the absolute square of the momentum operator matrix element between the lowest three bands for linearly polarized light propagating perpendicular to the helix axis (i.e. with z -polarisasi). Initially, for A g =C ⊥ =0, transitions between the ground and first bands are forbidden (as is to be expected for a unit cell with two equivalent wells resulting in a doubling of the first Brillouin zone, so it is in fact the same band). As the strength of the doubled period potential A g is increased with respect to B g , transitions become allowed away from q =0 as can be seen from Fig. 5a (following behaviour from the dotted red curve through to the solid blue curve). The parameters are swept through a resonance as we go from the solid to the dashed blue curve, wherein the situation changes drastically. To understand this behaviour, we must consider the special case of q =0. As we traverse this resonance, the energy of the Bloch function with q =0 constructed from the first excited state of the deeper well in the DQW unit cell (p -like) passes below the Bloch function constructed from the ground state in the shallower well (s -like). Consequently, the parity with respect to φ (which is a good quantum number only for q =0 or |q |=1/2) of the two excited states is exchanged resulting in the rapid switch from forbidden to allowed at q =0, wherein the z -polarized inter-subband matrix element becomes non-zero due to the operator \(\boldsymbol {\hat {P}}_{z}\) (see Eq. 15c) now coupling the even ground state with the odd first excited state. We therefore see the opposite behaviour for transitions between the ground and second band in Fig. 5b about q =0. While initially increasing A g allows transitions at q =0 between the ground state and the second excited state when it is p -like, beyond resonance (when the order of the s -like and p -like excited states are swapped) transitions are suppressed. See for example Ref. [88] for a clear picture of this interchange between the ordering of the even and the odd parity excited states. For transitions between the first and second band (Fig. 5c), we observe a large transition centred about q =0 due to the lifting of the m =± 1 degenerate states of the field-free helix by the superlattice potential. The presence of symmetry-breaking C ⊥ ruins the pristine parities of the states at the centre of the Brillouin zone and all transitions are allowed, as shown in the insets of Fig. 5.
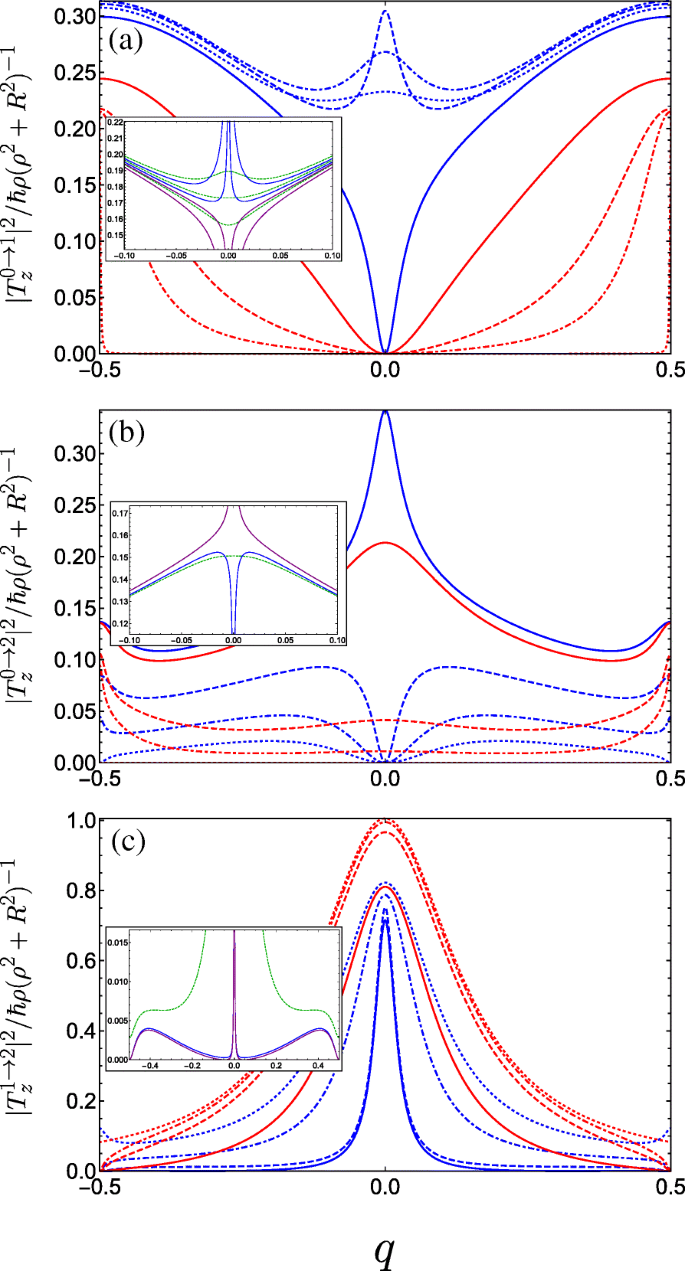
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by linearly z -polarized radiation and for a variety of parameter combinations spanning the first incident of resonance. The different blue curves keep A g =0.5 and C ⊥ =0 fixed and vary B g =0.1, 0.2, and 0.3 corresponding to dot-dashed, dashed, and solid. The different red curves keep B g =0.3 and C ⊥ =0 fixed while varying A g =0.05, 0.1 and 0.3 as dot-dashed, dashed, and solid, while the dotted blue (dotted red) plots the limiting case A g =0.5 &B g →0 (A g →0 &B g =0.3). a Transitions between the ground and first bands. The inset plots the behaviour for fixed A g =0.5 and changing B g crossing the resonant condition at B g =0.25 (see text) in a reduced q -range, ranging from upper blue B g =0.245, lower blue B g =0.249, upper purple B g =0.251, to lower purple B g =0.255. The dashed green curves are for small non-zero transverse field C ⊥ =0.05 ranging from B g =0.245 (upper curve) to B g =0.255 (lower curve) in increments of 0.05. b Plots transitions between the ground and second bands, the inset plots the behaviour close to resonance when A g =0.5; blue is B g =0.249, purple is B g =0.251, and dark green is at resonance with C ⊥ =0.05. c Plots transitions between the first and second bands, the parameters for the inset are the same as those in (b )
In Fig. 6, we plot the absolute square of the momentum operator matrix element for right-handed circularly polarized light which propagates along the helix axis, given by |T x +iT y | 2 . Notably, we observe a large anisotropy between the two halves of the first Brillouin zone, while the result for left-handed polarization is a mirror image to what we see in Fig. 6. Physically, this can be attributed to the conversion of the photon angular momenta to the translational motion of the free charge carriers projected onto the direction of the helix axis, with an unequal population of the excited subband in a preferential momentum direction controlled by the relative handedness of both the helix and the circular polarization of light. An intuitive mechanical analogue would be the rotary motion of Archimedes’ screw being converted into the linear motion of water along the direction of the screw axis dictated by the handedness of the thread. As such, our system of a double-gated nanohelix irradiated by circularly polarized light exhibits a photogalvanic effect, whereby one can choose the net direction of current by irradiating with either right- or left-handed circularly polarized light [44, 45, 89]. This differs from conventional one-dimensional superlattices, wherein the circular photogalvanic effect stems from the spin-orbit term appearing in the effective electron Hamiltonian and is consequently a weaker and hard-to-control phenomenon [90, 91]. The electric current induced by promoting electrons from the ground subband to an excited subband f via the absorption of circularly polarized light can be understood from the equation for the electric current contribution from the f th subband
$$ j_{f} =\frac{e}{2 \pi \rho} \int dq \left[ v_{f}(q) \tau_{f}(q) - v_{g}(q) \tau_{g} (q) \right] \Gamma_{CP}^{g \rightarrow f}(q), $$ (17)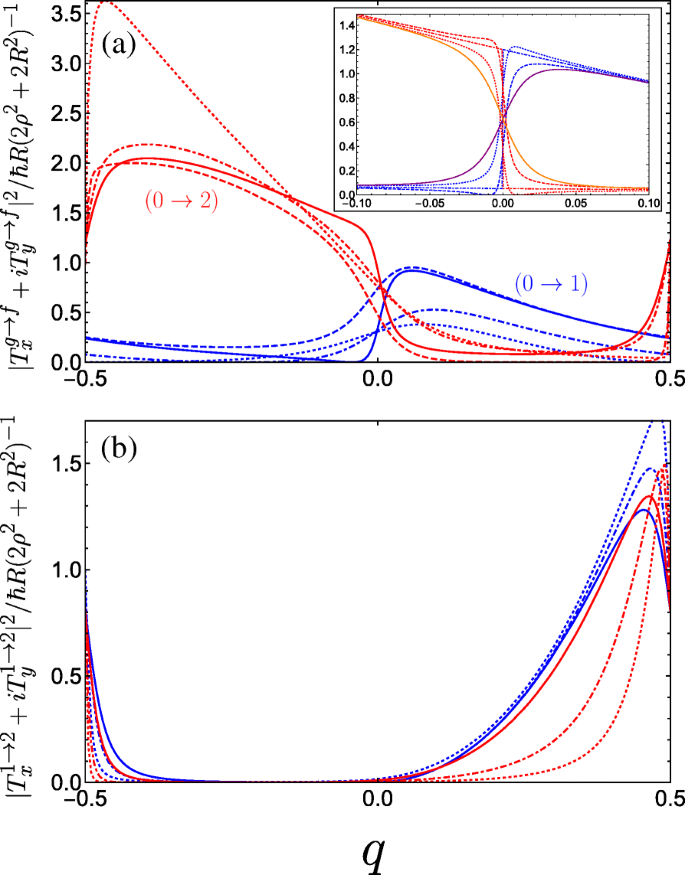
Square of the dimensionless momentum operator matrix element between the g th and f th subbands in the first Brillouin zone as a function of the dimensionless wave vector q of the electrons photoexcited by right-handed circularly polarized radiation |T x +iT y | 2 and for a variety of parameter combinations spanning the first incident of resonance. a The blue curves denote transitions between the ground and first band while the red curves denote transitions between the ground and second band, both with the following parameters:A g =0.5 and B g =0.3 for solid curves, A g =0.5 and B g =0.1 for dashed curves, A g =0.3 and B g =0.3 for dot-dashed curves, and A g =0.01 and B g =0.3 for dotted curves (as A g →0 the maximum of the 0→2 increases rapidly as it approaches q =− 1/2). The inset plots the behaviour as B g is tuned through resonance for A g =0.5; dotted is B g =0.24, dot-dashed is B g =0.25, and dashed is B g =0.26. The solid purple (orange) curve denotes transitions between the ground and first (second) band at resonance with C ⊥ =0.05 applied. b Plots transitions between the first and second bands. The different blue curves keep A g =0.5 fixed and vary B g =0, 0.2, and 0.3 corresponding to dotted, dot-dashed, and solid. The different red curves keep B g =0.3 fixed while varying A g =0.05, 0.1, and 0.3 as dotted, dot-dashed, and solid. We have omitted plots for C ⊥ ≠0 here as it yields no great qualitative change to the matrix elements
where \(v_{g,f}(q)=(\rho /\hbar)\partial \varepsilon _{g,f}/\partial q \) is the antisymmetric electron velocity v (q )=− v (− q ) (which we can deduce from the symmetric dispersion curves), τ g,f (q ) is a phenomenological relaxation time, and \(\Gamma _{CP}^{g \rightarrow f}(q)\) is the transition rate resulting from the optical perturbation of the electron system. Given that \(\Gamma _{CP}^{g \rightarrow f}(q) \propto |T_{x}^{g \rightarrow f} + i T_{y}^{g \rightarrow f}|^{2}\) for right-handed circularly polarized light where T x dan T y are given by Eqs. 16a and 16b, respectively. The anisotropy present in Fig. 6a enters Eq. 17 to yield a non-zero photocurrent. This current flows in the opposite direction for left-handed polarization. Such a circular photogalvanic effect is also exhibited in chiral carbon nanotubes under circularly polarized irradiation [92, 93], although tunability predominantly stems from manipulating the nanotube physical parameters, which are hard to control. The double-gated nanohelix system offers superior versatility by fully controlling the landscape of the superlattice potential, which can be used to tailor the non-equilibrium asymmetric distribution function of photoexcited carriers (as shown in Fig. 6 for inter-subband transitions between the three lowest subbands).
On a side note, we expect that (as with chiral carbon nanotubes [93–95]) the application of a magnetic field along the nanohelix axis can take up the role played by circularly polarized radiation, whereby the current is induced by a magnetic-field-induced asymmetric energy dispersion—which in turn produces an anisotropic electron velocity distribution across the two halves of the Brillouin zone.
In summary, we have shown that the system of a nanohelix between two aligned gates modelled as charged wires is a tunable binary superlattice. The band structure for this system exhibits a diverse behaviour, in particular revealing energy band crossings accessible via tuning the voltages on the gates. The application of an electric field normal to the plane defined by the gates and the helix axis introduces an additional parameter with which to open a band gap at these crossings. Engineering the band structure in situ with the externally induced superlattice potential along a nanohelix provides a clear advantage over conventional heterostructure superlattices with a DQW basis [96, 97]. Both systems can be used as high-responsivity photodetectors, wherein tailoring the band structure (to the so-called band-aligned basis [98–100]) can lead to a reduction in the accompanying dark current. Here control over the global depth of the quantum wells also permits versatility over the detection regime, which can lie within the THz range. We have also investigated the corresponding behaviour of electric dipole transitions between the lowest three subbands induced by both linearly and circularly polarized light, which additionally allows this system to be used for polarization sensitive detection. Finally, the ability to tune the system such that a degenerate excited state is optically accessible from the ground state, along with the inherent chirality present in the light-matter interactions, may make this a promising system for future quantum information processing applications [101]. It is hoped that with the advent of sophisticated nano-fabrication capabilities [102], fully controllable binary superlattice properties will be realized in a nanohelix and will undoubtedly contribute to novel optoelectronic applications.
Here, we show using matrix algebra that in the picture of a binary superlattice pairs of subbands touch at the Brillouin zone edges if A g =C ⊥ =0 and B g ≠0, as seen from the solid blue curves in Fig. 3a. Equation 5 is equivalent to the following N -by-N pentadiagonal matrix Hamiltonian with zeros on the leading sub- and superdiagonals:
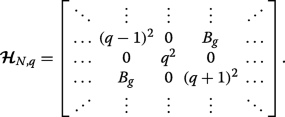 (18)
(18) Let us consider q =1/2 (we could alternatively take q =− 1/2) which makes the leading diagonal symmetric. We can then express this matrix Hamiltonian \(\widetilde {\mathcal {\boldsymbol {H}}}_{N} \equiv \boldsymbol {\mathcal {H}}_{N,q=1/2} \) in block form as
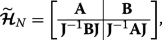 (19)
(19) where
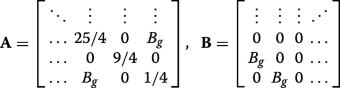 (20)
(20) are both of dimension N /2-by- N /2, and J is the exchange matrix. We may construct a matrix via permuting \(\boldsymbol {\mathcal {H}}_{N}\) with the N -by-N permutation matrix \(\boldsymbol {\mathcal {P}}_{N}\),
$$ \boldsymbol{\mathcal{P}}_{N} =\left[ \begin{array}{cccccc} 1 &0 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &\hdots &1 \\ 0 &1 &\hdots &\hdots &\hdots &0 \\ 0 &\hdots &\hdots &\hdots &1 &0 \\ \vdots &&&&&\vdots \\ 0 &\hdots &\hdots &1 &\hdots &0 \\ \end{array} \right], $$ (21)such that the permutation-similar matrix is
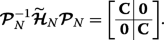 (22)
(22) Hence, the eigenvalues of \(\boldsymbol {\mathcal {P}}_{N}^{-1}\widetilde {\boldsymbol {\mathcal {H}}}_{N} \boldsymbol {\mathcal {P}}_{N}\), which are the same as the eigenvalues \(\widetilde {\boldsymbol {\mathcal {H}}}_{N}\), are double degenerate with the values given by the eigenvalue spectrum of the tridiagonal matrix C
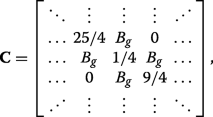 (23)
(23) which can also be expressed succinctly in terms of the previously defined matrices via \(\mathbf {C}=\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {A}\boldsymbol {\mathcal {P}}_{N/2}+\boldsymbol {\mathcal {P}}_{N/2}^{-1}\mathbf {B}\mathbf {J}\boldsymbol {\mathcal {P}}_{N/2}^{4}\). We can see that applying C ⊥ ≠0 (inset of Fig. 3a) or both C ⊥ dan A g ≠0 (inset of Fig. 3b) ruins the symmetry in the matrix Hamiltonian and prevents the existence of eigenvalues with multiplicity beyond unity, resulting in the appearance of band gaps.
As an example, let us specifically consider the case where p =2, wherein the matrices (12) and (13) become:
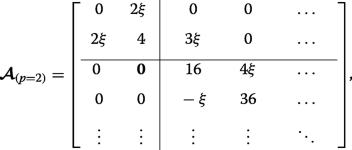 (24)
(24) dan
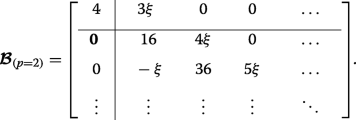 (25)
(25) This case corresponds to the crossings of the blue curves at the edge of the Brillouin zone in Fig. 3d (whereas p =0 results in crossings at q =0 in Fig. 3b). The lower eigenvalues are found exactly by diagonalizing each of the two finite matrices and they interlace, yielding \(\eta _{0,1,2} =2-\sqrt {4+4\xi ^{2}}, 4, 2+\sqrt {4+4\xi ^{2}}\). The infinite lower-right-hand block tridiagonal matrices coincide, thus the remaining double degenerate eigenvalues are found by approximately or numerically solving Det[D −η I ]=0.
The data for the figures all stem from numerically diagonalizing the matrix described by Eq. 5 and can readily be achieved in any numerical software package. With this in mind, the datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
bahan nano
Abstrak Circular dichroism (CD) adalah fenomena menarik yang berasal dari interaksi cahaya dengan molekul kiral atau struktur nano lain yang tidak memiliki simetri cermin dalam ruang tiga dimensi (3D) atau dua dimensi (2D). Sementara efek kiralitas optik yang dapat diamati sangat lemah di sebagian
Abstrak Dua desain filter warna metasurface (MCF) menggunakan konfigurasi aluminium dan lithium niobate (LN) diusulkan dan dipelajari secara numerik. Mereka dilambangkan sebagai metasurface aluminium merdu (TAM) dan metasurface LN merdu (TLNM), masing-masing. Konfigurasi MCF terdiri dari metasurfac
Abstrak Dalam makalah ini, TFET saluran SiGe berbentuk sirip tanpa doping (DF-TFET) diusulkan dan dipelajari. Untuk membentuk persimpangan tunneling garis tanpa doping efisiensi tinggi, saluran SiGe berbentuk sirip dan gerbang / sumber tumpang tindih diinduksi. Melalui metode ini, DF-TFET dengan ar
Komponen dan persediaan Arduino UNO × 1 sakelar sakelar spdt × 7 Sekrup Tutup Kepala Soket M3 x 8 × 15 M3 Nut × 3 Adafruit LCD Standar - 16x2 Putih di Atas Biru × 1 Kebuntuan 40mm × 4 Adafruit Silicone Cover Stranded-Core Wire - 30AWG