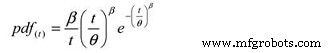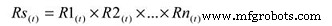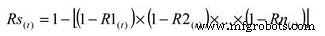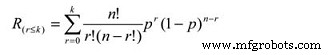Prinsip Rekayasa Keandalan untuk Insinyur Pabrik

Semakin, manajer dan insinyur yang bertanggung jawab untuk manufaktur dan kegiatan industri lainnya memasukkan fokus keandalan ke dalam rencana dan inisiatif strategis dan taktis mereka. Tren ini memengaruhi banyak area fungsional, termasuk desain dan pengadaan mesin/sistem, operasi pabrik, dan pemeliharaan pabrik.

Dengan asal-usulnya di industri penerbangan, rekayasa keandalan, sebagai suatu disiplin, secara historis difokuskan terutama untuk memastikan keandalan produk. Semakin banyak, metode ini digunakan untuk memastikan keandalan produksi pabrik dan peralatan manufaktur – seringkali sebagai pendukung lean manufacturing. Artikel ini memberikan pengantar yang paling relevan dan praktis dari metode ini untuk rekayasa keandalan pabrik, termasuk:

• Perhitungan keandalan dasar untuk tingkat kegagalan, MTBF, ketersediaan, dll.
• Pengantar distribusi eksponensial – landasan metode keandalan.
• Mengidentifikasi dependensi waktu kegagalan menggunakan sistem Weibull yang serbaguna.
• Mengembangkan sistem pengumpulan data lapangan yang efektif.

Sejarah Rekayasa Keandalan

Asal usul bidang rekayasa keandalan, setidaknya permintaan untuk itu, dapat ditelusuri kembali ke titik di mana manusia mulai bergantung pada mesin untuk mata pencahariannya. Noria, misalnya, adalah pompa kuno yang dianggap sebagai mesin canggih pertama di dunia. Memanfaatkan energi hidrolik dari aliran sungai atau aliran sungai, Noria menggunakan ember untuk memindahkan air ke palung, jembatan, dan perangkat distribusi lainnya untuk mengairi ladang dan menyediakan air untuk masyarakat.

Jika komunitas Noria gagal, orang-orang yang bergantung padanya untuk persediaan makanan mereka dalam bahaya. Bertahan hidup selalu menjadi sumber motivasi yang hebat untuk keandalan dan ketergantungan.

Sementara asal usul permintaannya sudah kuno, rekayasa keandalan sebagai disiplin teknis benar-benar berkembang seiring dengan pertumbuhan penerbangan komersial setelah Perang Dunia II. Dengan cepat menjadi jelas bagi para manajer perusahaan industri penerbangan bahwa kecelakaan itu buruk bagi bisnis. Karen Bernowski, editor Kemajuan Kualitas , terungkap dalam salah satu penelitian editorialnya tentang nilai media kematian dengan berbagai cara, yang dilakukan oleh profesor statistik MIT Arnold Barnett dan dilaporkan pada tahun 1994.

Barnett mengevaluasi jumlah artikel berita halaman depan New York Times per 1.000 kematian dengan berbagai cara. Dia menemukan bahwa kematian terkait kanker menghasilkan 0,02 artikel berita halaman depan per 1.000 kematian, pembunuhan menghasilkan 1,7 per 1.000 kematian, AIDS menghasilkan 2,3 per 1.000 kematian, dan kecelakaan terkait penerbangan menghasilkan 138,2 artikel kekalahan per 1.000 kematian!

Biaya dan sifat profil tinggi dari kecelakaan terkait penerbangan membantu memotivasi industri penerbangan untuk berpartisipasi besar dalam pengembangan disiplin rekayasa keandalan. Demikian juga, karena sifat kritis dari peralatan militer dalam pertahanan, teknik rekayasa keandalan telah lama digunakan untuk memastikan kesiapan operasional. Banyak standar kami di bidang teknik keandalan adalah Standar MIL atau berasal dari aktivitas militer.

Apa itu Rekayasa Keandalan?

Rekayasa keandalan berkaitan dengan umur panjang dan keandalan suku cadang, produk, dan sistem. Lebih pedih, ini tentang mengendalikan risiko. Rekayasa keandalan menggabungkan berbagai teknik analitik yang dirancang untuk membantu para insinyur memahami mode dan pola kegagalan bagian, produk, dan sistem ini. Secara tradisional, bidang rekayasa keandalan berfokus pada keandalan produk dan jaminan keandalan.

Dalam beberapa tahun terakhir, organisasi yang menerapkan mesin dan aset fisik lainnya dalam pengaturan produksi telah mulai menerapkan berbagai prinsip rekayasa keandalan untuk tujuan keandalan produksi dan jaminan keandalan.

Semakin banyak, organisasi produksi menerapkan teknik rekayasa keandalan seperti Reliability-Centered Maintenance (RCM), termasuk mode kegagalan dan analisis efek (dan kekritisan) (FMEA,FMECA), analisis akar penyebab (RCA), pemeliharaan berbasis kondisi, skema perencanaan kerja yang ditingkatkan, dll. Organisasi yang sama ini mulai mengadopsi desain siklus hidup dan strategi pengadaan, skema manajemen perubahan, serta alat dan teknik canggih lainnya untuk mengendalikan akar penyebab keandalan yang buruk.

Namun, adopsi aspek rekayasa keandalan yang lebih kuantitatif oleh komunitas jaminan keandalan produksi berjalan lambat. Hal ini sebagian disebabkan oleh kerumitan yang dirasakan dari teknik-teknik tersebut dan sebagian lagi karena kesulitan dalam memperoleh data yang berguna.

Aspek kuantitatif rekayasa keandalan mungkin, di permukaan, tampak rumit dan menakutkan. Namun, pada kenyataannya, pemahaman yang relatif mendasar tentang metode yang paling mendasar dan dapat diterapkan secara luas dapat memungkinkan insinyur keandalan pabrik memperoleh pemahaman yang lebih jelas tentang di mana masalah terjadi, sifat dan dampaknya terhadap proses produksi – setidaknya secara kuantitatif. akal.

Digunakan dengan benar, alat dan metode rekayasa keandalan kuantitatif memungkinkan rekayasa keandalan pabrik untuk lebih efektif menerapkan kerangka kerja yang disediakan oleh RCM, RCA, dll., dengan menghilangkan beberapa dugaan yang terlibat dengan aplikasi mereka sebaliknya. Namun, para insinyur harus sangat pintar dalam penerapan metode mereka.

Mengapa? Konteks operasi dan lingkungan proses produksi menggabungkan lebih banyak variabel daripada dunia jaminan keandalan produk yang agak satu dimensi. Hal ini disebabkan oleh pengaruh gabungan dari rekayasa desain, pengadaan, produksi/operasi, pemeliharaan, dll., dan kesulitan dalam menciptakan pengujian dan eksperimen yang efektif untuk memodelkan aspek multidimensi dari lingkungan produksi yang khas.

Terlepas dari meningkatnya kesulitan dalam menerapkan metode keandalan kuantitatif di lingkungan produksi, tetap saja bermanfaat untuk mendapatkan pemahaman yang baik tentang alat dan menerapkannya jika sesuai. Data kuantitatif membantu untuk menentukan sifat dan besarnya masalah/peluang, yang memberikan visi keandalan dalam penerapan alat rekayasa keandalan lainnya.

Artikel ini akan memberikan pengenalan metode rekayasa keandalan paling dasar yang berlaku untuk insinyur pabrik yang tertarik pada jaminan keandalan produksi. Ini mengandaikan pemahaman dasar tentang aljabar, teori probabilitas dan statistik univariat berdasarkan distribusi Gaussian (normal) (misalnya ukuran tendensi sentral, ukuran dispersi dan variabilitas, interval kepercayaan, dll.).

Harus dijelaskan bahwa makalah ini adalah pengantar singkat untuk metode reliabilitas. Ini sama sekali bukan survei komprehensif tentang metode rekayasa keandalan, juga bukan hal baru atau tidak konvensional. Metode yang dijelaskan di sini secara rutin digunakan oleh insinyur keandalan dan merupakan konsep pengetahuan inti bagi mereka yang mengejar sertifikasi profesional oleh American Society for Quality (ASQ) sebagai insinyur keandalan (CRE).

Beberapa buku tentang rekayasa keandalan tercantum dalam daftar pustaka artikel ini. Penulis artikel ini telah menemukan Metode Keandalan untuk Insinyur oleh K.S. Krishnamoorthi dan Statistik Keandalan oleh Robert Dovich menjadi referensi yang sangat berguna dan ramah pengguna pada subjek metode rekayasa keandalan. Keduanya diterbitkan oleh ASQ Press.

Sebelum membahas metode, Anda harus membiasakan diri dengan nomenklatur teknik keandalan. Untuk kenyamanan, daftar istilah dan definisi kunci yang sangat singkat disediakan dalam lampiran artikel ini. Untuk definisi istilah dan nomenklatur keandalan yang lebih lengkap, lihat MIL-STD-721 dan standar terkait lainnya. Definisi yang terkandung dalam lampiran berasal dari MIL-STD-721.

Konsep Matematika Dasar dalam Rekayasa Keandalan

Banyak konsep matematika berlaku untuk rekayasa keandalan, terutama dari bidang probabilitas dan statistik. Demikian juga, banyak distribusi matematika dapat digunakan untuk berbagai tujuan, termasuk distribusi Gaussian (normal), distribusi log-normal, distribusi Rayleigh, distribusi eksponensial, distribusi Weibull dan banyak lainnya.

Untuk tujuan pengenalan singkat ini, kami akan membatasi diskusi kami pada distribusi eksponensial dan distribusi Weibull, dua yang paling banyak diterapkan pada rekayasa keandalan. Untuk kepentingan singkat dan kesederhanaan, konsep matematika penting seperti distribusi kecocokan dan interval kepercayaan telah dikecualikan.

Tingkat kegagalan dan waktu rata-rata antara/ke kegagalan (MTBF/MTTF)

Tujuan pengukuran reliabilitas kuantitatif adalah untuk menentukan tingkat kegagalan relatif terhadap waktu dan untuk memodelkan tingkat kegagalan tersebut dalam distribusi matematis untuk tujuan memahami aspek kuantitatif kegagalan. Blok bangunan yang paling dasar adalah tingkat kegagalan, yang diperkirakan menggunakan persamaan berikut:

Dimana:
=Tingkat kegagalan (kadang-kadang disebut sebagai tingkat bahaya)
T =Total waktu berjalan/siklus/mil/dll. selama periode investigasi untuk item yang gagal dan tidak gagal.
r =Jumlah total kegagalan yang terjadi selama periode investigasi.

Misalnya, jika lima motor listrik beroperasi untuk total waktu 50 tahun dengan lima kegagalan fungsional selama periode tersebut, tingkat kegagalannya adalah 0,1 kegagalan per tahun.

Konsep lain yang sangat mendasar adalah waktu rata-rata antara/ke kegagalan (MTBF/MTTF). Satu-satunya perbedaan antara MTBF dan MTTF adalah bahwa kami menggunakan MTBF saat mengacu pada item yang diperbaiki saat gagal. Untuk barang yang dibuang begitu saja dan diganti, kami menggunakan istilah MTTF. Perhitungannya sama.

Perhitungan dasar untuk memperkirakan waktu rata-rata antara kegagalan (MTBF) dan waktu rata-rata untuk kegagalan (MTTF), kedua ukuran tendensi sentral, hanyalah kebalikan dari fungsi tingkat kegagalan. Ini dihitung menggunakan persamaan berikut.

Dimana:
=Waktu rata-rata antara/sampai kegagalan
T =Total waktu berjalan/siklus/mil/dll. selama periode investigasi untuk item yang gagal dan tidak gagal.
r =Jumlah total kegagalan yang terjadi selama periode investigasi.

MTBF untuk contoh motor listrik industri kami adalah 10 tahun, yang merupakan kebalikan dari tingkat kegagalan motor. Kebetulan, kami akan memperkirakan MTBF untuk motor listrik yang dibangun kembali setelah kegagalan. Untuk motor yang lebih kecil yang dianggap sekali pakai, kami akan menyatakan ukuran tendensi sentral sebagai MTTF.

Tingkat kegagalan adalah komponen dasar dari banyak perhitungan keandalan yang lebih kompleks. Tergantung pada desain mekanik/listrik, konteks operasi, lingkungan dan/atau efektivitas perawatan, tingkat kegagalan mesin sebagai fungsi waktu dapat menurun, tetap konstan, meningkat secara linier atau meningkat secara geometris (Gambar 1). Pentingnya tingkat kegagalan vs. waktu akan dibahas lebih rinci nanti.

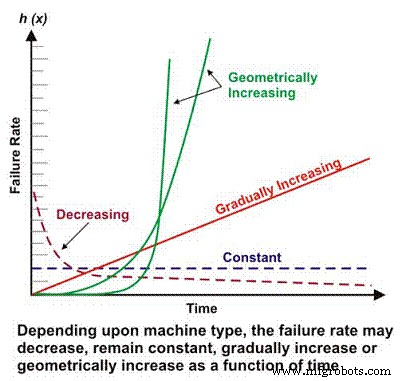
Gambar 1. Perbedaan Tingkat Kegagalan vs. Skenario Waktu

Kurva 'Bathtub'

Individu yang hanya menerima pelatihan dasar dalam probabilitas dan statistik mungkin paling akrab dengan distribusi Gaussian atau normal, yang dikaitkan dengan kurva kepadatan probabilitas berbentuk lonceng yang sudah dikenal. Distribusi Gaussian umumnya berlaku untuk kumpulan data di mana dua ukuran tendensi sentral yang paling umum, mean dan median, kira-kira sama.

Anehnya, meskipun keserbagunaan distribusi Gaussian dalam memodelkan probabilitas untuk fenomena mulai dari skor tes standar hingga berat lahir bayi, itu bukan distribusi dominan yang digunakan dalam rekayasa keandalan. Distribusi Gaussian memiliki tempatnya dalam mengevaluasi karakteristik kegagalan mesin dengan mode kegagalan dominan, tetapi distribusi utama yang digunakan dalam rekayasa keandalan adalah distribusi eksponensial.

Saat mengevaluasi karakteristik keandalan dan kegagalan mesin, kita harus mulai dengan kurva "bak mandi" yang banyak difitnah, yang mencerminkan tingkat kegagalan vs. waktu (Gambar 2). Dalam konsepnya, kurva bak mandi secara efektif menunjukkan tiga karakteristik tingkat kegagalan dasar mesin:menurun, konstan, atau meningkat. Sayangnya, kurva bak mandi telah dikritik keras dalam literatur teknik pemeliharaan karena gagal untuk secara efektif memodelkan tingkat kegagalan karakteristik untuk sebagian besar mesin di pabrik industri, yang umumnya benar pada tingkat makro.

Kebanyakan mesin menghabiskan hidup mereka di awal kehidupan, atau kematian bayi, dan/atau daerah tingkat kegagalan konstan dari kurva bak mandi. Kami jarang melihat kegagalan berbasis waktu sistemik di mesin industri. Terlepas dari keterbatasannya dalam memodelkan tingkat kegagalan mesin industri biasa, kurva bak mandi adalah alat yang berguna untuk menjelaskan konsep dasar rekayasa keandalan.

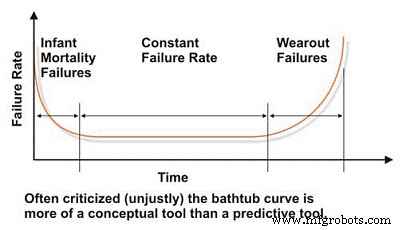
Gambar 2. Kurva 'Bathtub' yang Banyak Difitnah

Tubuh manusia adalah contoh yang sangat baik dari sistem yang mengikuti kurva bak mandi. Orang-orang, dan spesies organik lainnya dalam hal ini, cenderung mengalami tingkat kegagalan (kematian) yang tinggi selama tahun-tahun pertama kehidupan mereka, terutama beberapa tahun pertama, tetapi angka tersebut menurun seiring dengan bertambahnya usia anak. Dengan asumsi seseorang mencapai pubertas dan bertahan di masa remajanya, angka kematiannya menjadi cukup konstan dan tetap di sana sampai penyakit yang bergantung pada usia (waktu) mulai meningkatkan angka kematian (keausan).

Banyak pengaruh yang mempengaruhi angka kematian, termasuk perawatan prenatal dan nutrisi ibu, kualitas dan ketersediaan perawatan medis, lingkungan dan nutrisi, pilihan gaya hidup dan, tentu saja, predisposisi genetik. Faktor-faktor ini dapat secara metaforis dibandingkan dengan faktor-faktor yang mempengaruhi umur mesin. Desain dan pengadaan analog dengan kecenderungan genetik; instalasi dan commissioning analog dengan perawatan prenatal dan nutrisi ibu; dan pilihan gaya hidup serta ketersediaan perawatan medis analog dengan efektivitas pemeliharaan dan kontrol proaktif atas kondisi operasi.

Distribusi eksponensial

Distribusi eksponensial, rumus prediksi keandalan yang paling dasar dan banyak digunakan, memodelkan mesin dengan tingkat kegagalan konstan, atau bagian datar dari kurva bak mandi. Sebagian besar mesin industri menghabiskan sebagian besar hidupnya dalam tingkat kegagalan yang konstan, sehingga dapat diterapkan secara luas. Di bawah ini adalah persamaan dasar untuk memperkirakan keandalan mesin yang mengikuti distribusi eksponensial, di mana tingkat kegagalan adalah konstan sebagai fungsi waktu.

Dimana:
R(t) =Perkiraan keandalan untuk periode waktu, siklus, mil, dll. (t).
e =Basis logaritma natural (2.718281828)
=Laju kegagalan (1/MTBF, atau 1/MTTF)

Dalam contoh motor listrik kami, jika Anda mengasumsikan tingkat kegagalan konstan, kemungkinan menjalankan motor selama enam tahun tanpa kegagalan, atau keandalan yang diproyeksikan, adalah 55 persen. Ini dihitung sebagai berikut:
R(6) =2,718281828-(0,1* 6)
R(6) =0,5488 =~ 55%

Dengan kata lain, setelah enam tahun, sekitar 45% dari populasi motor identik yang beroperasi dalam aplikasi yang identik kemungkinan besar akan gagal. Perlu ditegaskan kembali pada titik ini bahwa perhitungan ini memproyeksikan probabilitas untuk suatu populasi. Setiap individu tertentu dari populasi bisa gagal pada hari pertama operasi sementara individu lain bisa bertahan 30 tahun. Itulah sifat proyeksi keandalan probabilistik.

Karakteristik dari distribusi eksponensial adalah MTBF terjadi pada titik di mana keandalan yang dihitung adalah 36,78%, atau titik di mana 63,22% mesin telah gagal. Dalam contoh motor kami, setelah 10 tahun, 63,22% motor dari populasi motor identik yang melayani dalam aplikasi identik dapat diperkirakan gagal. Dengan kata lain, tingkat kelangsungan hidup adalah 36,78% dari populasi.

Kita sering berbicara tentang masa pakai bantalan yang diproyeksikan sebagai masa pakai L10. Ini adalah titik waktu di mana 10% dari populasi bantalan diharapkan gagal (tingkat kelangsungan hidup 90%). Pada kenyataannya, hanya sebagian kecil dari bantalan yang benar-benar bertahan hingga titik L10. Kami telah menerimanya sebagai masa pakai objektif untuk bantalan ketika mungkin kami harus mengarahkan pandangan kami pada titik L63.22, yang menunjukkan bahwa bantalan kami rata-rata tahan lama, untuk proyeksi MTBF – dengan asumsi, tentu saja, bahwa bantalan mengikuti distribusi eksponensial. Kami akan membahas masalah itu nanti di bagian analisis Weibull di artikel.

Fungsi kepadatan probabilitas (pdf), atau distribusi kehidupan, adalah persamaan matematis yang mendekati distribusi frekuensi kegagalan. Ini adalah pdf, atau distribusi frekuensi hidup, yang menghasilkan kurva berbentuk lonceng yang sudah dikenal dalam distribusi Gaussian, atau normal. Di bawah ini adalah pdf untuk distribusi eksponensial.

Dimana:
pdf(t) =distribusi frekuensi hidup untuk waktu tertentu (t)
e =Basis logaritma natural (2.718281828)
=Laju kegagalan (1/MTBF, atau 1/MTTF)

Dalam contoh motor listrik kami, kemungkinan kegagalan aktual dalam tiga tahun dihitung sebagai berikut:
pdf(3) =01. * 2.718281828-(0.1* 3)
pdf(3) =0,1 * 0,7408
pdf(3) =.07408 =~ 7.4%

Dalam contoh kita, jika kita mengasumsikan tingkat kegagalan konstan, yang mengikuti distribusi eksponensial, distribusi umur, atau pdf untuk motor listrik industri, dinyatakan dalam Gambar 3. Jangan bingung dengan sifat menurun dari fungsi pdf. Ya, tingkat kegagalannya konstan, tetapi pdf secara matematis mengasumsikan kegagalan tanpa penggantian, sehingga populasi dari mana kegagalan dapat terjadi terus berkurang – mendekati nol secara asimtotik.

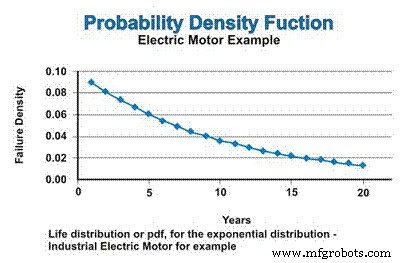
Gambar 3. Fungsi Densitas Probabilitas (pdf)

Fungsi distribusi kumulatif (cdf) hanyalah jumlah kumulatif kegagalan yang mungkin diharapkan selama periode waktu tertentu. Untuk distribusi eksponensial, laju kegagalan konstan, sehingga laju relatif di mana komponen gagal ditambahkan ke cdf tetap konstan. Namun, karena populasi menurun sebagai akibat dari kegagalan, jumlah sebenarnya dari kegagalan yang diperkirakan secara matematis menurun sebagai fungsi dari populasi yang menurun. Sama seperti pdf asimtotik mendekati nol, cdf asimtotis mendekati satu (Gambar 4).

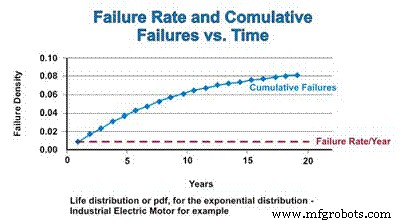
Gambar 4. Laju Kegagalan dan Fungsi Distribusi Kumulatif

Bagian tingkat kegagalan yang menurun dari kurva bak mandi, yang sering disebut wilayah kematian bayi, dan wilayah keausan akan dibahas pada bagian berikut yang membahas distribusi Weibull serbaguna.

Distribusi Weibull

Awalnya dikembangkan oleh Wallodi Weibull, seorang matematikawan Swedia, analisis Weibull dengan mudah merupakan distribusi paling serbaguna yang digunakan oleh para insinyur keandalan. Meskipun disebut distribusi, sebenarnya adalah alat yang memungkinkan insinyur keandalan untuk terlebih dahulu mengkarakterisasi fungsi kepadatan probabilitas (distribusi frekuensi kegagalan) dari sekumpulan data kegagalan untuk mengkarakterisasi kegagalan sebagai masa pakai awal, konstan (eksponensial) atau aus. (Gaussian atau log normal) dengan memplot data waktu hingga kegagalan pada kertas plot khusus dengan log waktu/siklus/mil hingga kegagalan yang diplot dengan sumbu X skala log versus persentase kumulatif populasi yang diwakili oleh setiap kegagalan pada log -sumbu Y berskala log (Gambar 5).

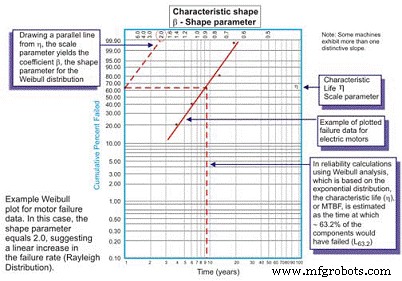
Gambar 5. Plot Weibull Sederhana – Beranotasi

Setelah diplot, kemiringan linier dari kurva yang dihasilkan merupakan variabel penting, yang disebut parameter bentuk, yang diwakili oleh , yang digunakan untuk menyesuaikan distribusi eksponensial agar sesuai dengan sejumlah besar distribusi kegagalan. Secara umum, jika koefisien , atau parameter bentuk, kurang dari 1,0, distribusi menunjukkan kehidupan awal, atau kegagalan kematian bayi. Jika parameter bentuk melebihi sekitar 3,5, data bergantung pada waktu dan menunjukkan kegagalan keausan.

Kumpulan data ini biasanya mengasumsikan distribusi Gaussian, atau normal. Ketika koefisien â meningkat di atas ~ 3,5, distribusi berbentuk lonceng mengencang, menunjukkan peningkatan kurtosis (puncak di bagian atas kurva) dan standar deviasi yang lebih kecil. Banyak kumpulan data akan menunjukkan dua atau bahkan tiga wilayah berbeda.

Adalah umum bagi insinyur keandalan untuk memplot, misalnya, satu kurva yang mewakili parameter bentuk selama proses berjalan dan kurva lain untuk mewakili tingkat kegagalan yang konstan atau meningkat secara bertahap. Dalam beberapa kasus, kemiringan linier ketiga yang berbeda muncul untuk mengidentifikasi bentuk ketiga, wilayah keausan.

Dalam hal ini, pdf dari data kegagalan sebenarnya mengasumsikan bentuk kurva bak mandi yang sudah dikenal (Gambar 6). Sebagian besar peralatan mekanis yang digunakan di pabrik, bagaimanapun, menunjukkan daerah kematian bayi dan daerah tingkat kegagalan yang konstan atau meningkat secara bertahap. Jarang terlihat kurva yang mewakili keausan muncul. Kehidupan karakteristik, atau (huruf kecil Yunani "Eta"), adalah pendekatan Weibull dari MTBF. Itu selalu merupakan fungsi waktu, mil atau siklus di mana 63,21% unit yang dievaluasi gagal, yang merupakan MTBF/MTTF untuk distribusi eksponensial.

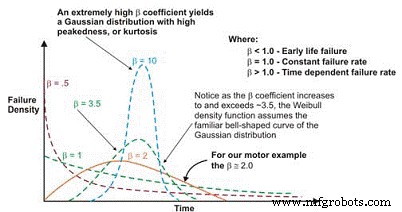
Gambar 6. Tergantung pada parameter bentuk, kerapatan kegagalan Weibull kurva dapat mengasumsikan beberapa distribusi, yang membuatnya sangat fleksibel untuk rekayasa keandalan.

Sebagai peringatan untuk mengikat alat ini kembali ke keunggulan dalam keunggulan pemeliharaan dan operasi, jika kita ingin lebih efektif mengontrol fungsi pemaksaan yang menyebabkan kegagalan mekanis pada bantalan, roda gigi, dll., seperti pelumasan, kontrol kontaminasi, penyelarasan, keseimbangan, operasi yang sesuai, dll., lebih banyak mesin akan benar-benar mencapai umur kelelahannya. Mesin yang mencapai umur kelelahannya akan menunjukkan karakteristik keausan yang sudah dikenal.

Menggunakan koefisien untuk menyesuaikan persamaan tingkat kegagalan sebagai fungsi waktu menghasilkan persamaan umum berikut:

Dimana:
h(t) =Tingkat kegagalan (atau tingkat bahaya) untuk waktu tertentu (t)
e =Basis logaritma natural (2.718281828)
=Estimasi MTBF/MTTF
=Parameter bentuk Weibull dari plot.

Dan, fungsi keandalan berikut:

Dimana:
R(t) =Perkiraan keandalan untuk periode waktu, siklus, mil, dll. (t)
e =Basis logaritma natural (2.718281828)
=Estimasi MTBF/MTTF
=Parameter bentuk Weibull dari plot.

Dan, berikut fungsi kepadatan probabilitas (pdf):

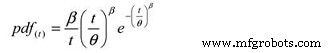
Dimana:
pdf(t) =Estimasi fungsi densitas probabilitas untuk suatu periode waktu,
siklus, mil, dll. (t)
e =Basis logaritma natural (2.718281828)
=Estimasi MTBF/MTTF
=Parameter bentuk Weibull dari plot.

Perlu dicatat bahwa ketika sama dengan 1,0, distribusi Weibull mengambil bentuk distribusi eksponensial yang menjadi dasarnya.

Bagi yang belum tahu, matematika yang diperlukan untuk melakukan analisis Weibull mungkin terlihat menakutkan. Tapi begitu Anda memahami mekanisme rumusnya, matematikanya sangat sederhana. Selain itu, perangkat lunak akan melakukan sebagian besar pekerjaan untuk kita saat ini, tetapi penting untuk memiliki pemahaman tentang teori yang mendasarinya sehingga insinyur keandalan pabrik dapat secara efektif menerapkan teknik analisis Weibull yang kuat.

Dalam contoh motor listrik yang telah kita bahas sebelumnya, kita sebelumnya mengasumsikan distribusi eksponensial. Namun, jika analisis Weibull mengungkapkan kegagalan umur awal dengan menghasilkan parameter bentuk 0,5, perkiraan keandalan pada waktu enam tahun akan ~46%, bukan ~55% yang diperkirakan dengan asumsi distribusi eksponensial. Untuk mengurangi kegagalan keausan, kami perlu bersandar pada pemasok kami untuk memberikan kualitas dan keandalan yang lebih baik dibangun dan disampaikan, menyimpan motor lebih baik untuk menghindari karat, korosi, resah dan mekanisme keausan statis lainnya, dan melakukan pekerjaan pemasangan yang lebih baik. dan memulai mesin baru atau yang dibuat ulang.

Sebaliknya, jika analisis Weibull mengungkapkan bahwa motor menunjukkan sebagian besar kegagalan terkait keausan, menghasilkan parameter bentuk 5.0, perkiraan keandalan pada waktu enam tahun akan ~ 93%, bukannya ~ 55% yang diperkirakan dengan asumsi distribusi eksponensial. Untuk kegagalan keausan yang bergantung pada waktu, kami dapat melakukan perombakan atau penggantian terjadwal dengan asumsi kami memiliki perkiraan yang baik tentang MTBF/MTTF setelah kami mencapai wilayah keausan dan standar deviasi yang cukup kecil sehingga dapat membuat keputusan pembangunan kembali/penggantian yang sangat percaya diri. tidak terlalu mahal.

Dalam contoh motor kami, dengan asumsi parameter bentuk 5.0, tingkat kegagalan mulai meningkat dengan cepat setelah sekitar lima atau enam tahun, jadi kami mungkin ingin mengedit data kami untuk hanya fokus pada wilayah keausan saat memperkirakan penggantian atau pembangunan kembali berbasis waktu waktu. Sebagai alternatif, kita dapat meningkatkan desain, menargetkan mode kegagalan dominan dengan tujuan mengurangi gangguan "tegangan-kekuatan". Dengan kata lain, kita dapat mencoba menghilangkan kelemahan mesin melalui modifikasi desain, dengan tujuan untuk menghilangkan apa pun yang menyebabkan kegagalan yang bergantung pada waktu.

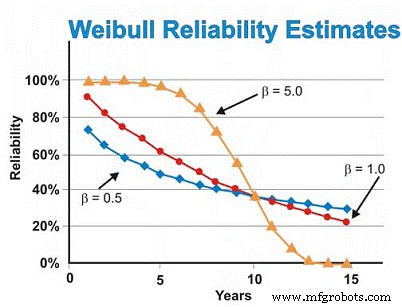
Dengan asumsi semuanya konstan, kecuali parameter bentuk , Gambar 7 mengilustrasikan perbedaan yang dimiliki parameter bentuk pada estimasi keandalan dengan asumsi nilai bentuk 0,5 (kehidupan awal), 1,0 (konstan, atau eksponensial) dan 5,0 (keausan) untuk rentang perkiraan waktu. Grafik ini secara visual menggambarkan konsep peningkatan risiko vs waktu (β =0,5), risiko konstan vs waktu (β =1,0) dan peningkatan risiko vs waktu (β =5).

Gambar 7. Berbagai Proyeksi Keandalan sebagai Fungsi Waktu untuk Berbagai Parameter Bentuk Weibull

Plot Weibull Multi-Lereng

Seringkali, ketika menggambar garis regresi yang paling sesuai melalui titik-titik data pada plot Weibull, koefisien korelasinya buruk, yang berarti titik-titik data aktual menyimpang jauh dari garis regresi. Hal ini dinilai dengan memeriksa koefisien korelasi R, atau lebih konservatif, R2, yang menunjukkan variabilitas data. Ketika korelasi buruk, insinyur keandalan harus memeriksa data untuk mengevaluasi apakah ada dua atau lebih pola, yang dapat menunjukkan perbedaan besar dalam mode kegagalan, konteks operasi, dll. Seringkali, ini menghasilkan dua atau lebih perkiraan beta (Gambar 8).

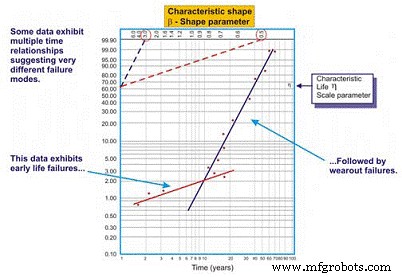
Gambar 8. Contoh Plot Weibull Multi-beta

Seperti yang kita lihat dalam contoh kita di Gambar 8, kumpulan data bekerja lebih baik ketika dua garis regresi yang berbeda ditarik. Baris pertama, menunjukkan parameter bentuk beta 0,5, menunjukkan kegagalan kehidupan awal. Baris kedua menunjukkan bentuk beta 3.0, menunjukkan bahwa risiko kegagalan meningkat sebagai fungsi waktu. Adalah umum untuk peralatan yang kompleks, terutama peralatan mekanis, untuk mengalami kegagalan "run-in" ketika baru atau baru saja dibangun kembali. Dengan demikian, risiko kegagalan paling tinggi hanya setelah start-up awal.

Setelah sistem bekerja melalui periode berjalannya, yang dapat memakan waktu beberapa menit, jam, hari, minggu, bulan atau tahun, tergantung pada jenis sistem, sistem memasuki pola risiko yang berbeda. Dalam contoh ini, sistem memasuki periode di mana risiko kegagalan meningkat sebagai fungsi waktu setelah sistem keluar dari periode run-in.

Multi-beta menawarkan insinyur keandalan perkiraan risiko yang lebih tepat sebagai fungsi waktu. Berbekal pengetahuan ini, dia berada pada posisi yang lebih baik untuk mengambil tindakan mitigasi. Misalnya, selama periode masa pakai awal, kami cenderung meningkatkan presisi yang kami gunakan untuk membuat/membangun kembali, memasang, dan memulai. Selain itu, kami mungkin menambahkan teknik pemantauan dan/atau meningkatkan frekuensi pemantauan kami selama periode berisiko tinggi. Setelah periode berjalan, kami mungkin memperkenalkan teknik pemantauan yang ditargetkan pada kegagalan keausan bergantung waktu yang diyakini memengaruhi sistem, meningkatkan frekuensi pemantauan yang sesuai, atau menjadwalkan tindakan pemeliharaan preventif "sulit" dalam beberapa kasus.

Memperkirakan Keandalan Sistem

Setelah keandalan komponen atau mesin telah ditetapkan relatif terhadap konteks operasi dan waktu misi yang diperlukan, insinyur pabrik harus menilai keandalan sistem atau proses. Sekali lagi, demi singkatnya dan kesederhanaan, kita akan membahas perkiraan keandalan sistem untuk sistem redundan seri, paralel, dan beban bersama (sistem r/n).

Sistem Seri
Sebelum membahas sistem seri, kita harus membahas diagram blok keandalan. Bukan alat yang rumit untuk digunakan, diagram blok keandalan hanya memetakan proses dari awal hingga akhir. Untuk sistem seri, Subsistem A diikuti oleh Subsistem B dan seterusnya. Dalam sistem seri, kemampuan untuk menggunakan Subsistem B bergantung pada status operasi Subsistem A. Jika Subsistem A tidak beroperasi, sistem akan mati terlepas dari kondisi Subsistem B (Gambar 9).

To calculate the system reliability for a serial process, you only need to multiply the estimated reliability of Subsystem A at time (t) by the estimated reliability of Subsystem B at time (t). The basic equation for calculating the system reliability of a simple series system is:

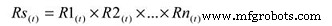
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

So, for a simple system with three subsystems, or sub-functions, each having an estimated reliability of 0.90 (90%) at time (t), the system reliability is calculated as 0.90 X 0.90 X 0.90 =0.729, or about 73%.

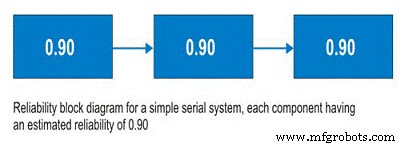
Figure 9. Simple Serial System

Parallel Systems
Often, design engineers will incorporate redundancy into critical machines. Reliability engineers call these parallel systems. These systems may be designed as active parallel systems or standby parallel systems. The block diagram for a simple two component parallel system is shown in Figure 10.

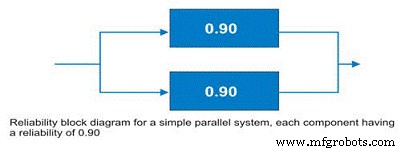
Figure 10. Simple parallel system – the system reliability is increased to 99% due to the redundancy.

To calculate the reliability of an active parallel system, where both machines are running, use the following simple equation:

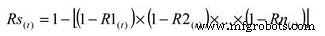
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

The simple parallel system in our example with two components in parallel, each having a reliability of 0.90, has a total system reliability of 1 – (0.1 X 0.1) =0.99. So, the system reliability was significantly improved.

There are some shortcut methods for calculating parallel system reliability when all subsystems have the same estimated reliability. More often, systems contain parallel and serial subcomponents as depicted in Figure 11. The calculation of standby systems requires knowledge about the reliability of the switching mechanism. In the interest of simplicity and brevity, this topic will be reserved for a future article.

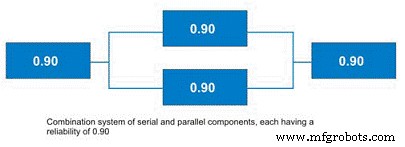
Figure 11. Combination System with Parallel and Serial Elements

r out of n Systems (r/n Systems)
An important concept to plant reliability engineers is the concept of r/n systems. These systems require that r units from a total population in n be available for use. A great industrial example is coal pulverizers in an electric power generating plant. Often, the engineers design this function in the plant using an r/n approach. For instance, a unit has four pulverizers and the unit requires that three of the four be operable to run at the unit’s full load (see Figure 12).

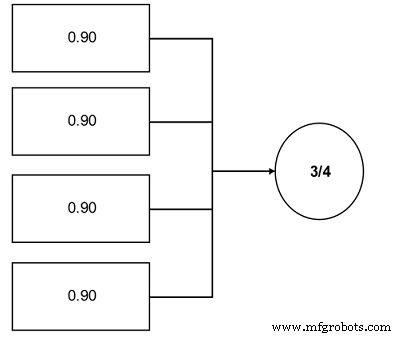
Figure 12. Simple r/n system example – Three of the four components are required.

The reliability calculation for an r/n system can be reduced to a simple cumulative binomial distribution calculation, the formula for which is:

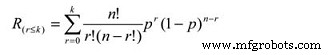
Where:
Rs =System reliability given the actual number of failures (r) is less than or equal the maximum allowable (k)
r =The actual number of failures
k =The maximum allowable number of failures
n =The total number of units in the system
p =The probability of survival, or the subcomponent reliability for a given time (t).

This equation is somewhat more complicated. In our pulverizer example, assuming a subcomponent reliability of 0.90, the equation works out as a summation of the following:
P(0) =0.6561
P(1) =0.2916

So, the likelihood of completing the mission time (t) is 0.9477 (0.6561 + 0.2916), or approximately 95%.

Field Data Collection
To employ the reliability analysis methods described herein, the engineer requires data. It is imperative to establish field data collection systems to support your reliability management initiatives. Likewise, as much as possible, you’ll want to employ common nomenclature and units so that your data can be parsed effectively for more detailed analysis. Collect the following information:

• Basic System Information
• Operating Context
• Environmental Context
• Failure Data

A good general system for data collection is described in the IEC standard 300-3-2. In addition to providing instructions for collecting field data, it provides a standard taxonomy of failure modes. Other taxonomies have been established, but the IEC standard represents a good starting point for your organization to define its own. Likewise, DOE standard NE-1004-92 offers a very nice standard nomenclature of failure causes.

An important benefit derived from your efforts to collect good field data is that it enables you to break the “random trap.” As I mentioned earlier, the bathtub curve has been much maligned – particularly in the Reliability-Centered Maintenance literature. While it’s true that Weibull analysis reveals that few complex mechanical systems exhibit time-dependent wearout failures, the reason, at least in part, is due to the fact that the reliability of complex systems is affected by a wide variety of failure modes and mechanisms.

When these are lumped together, there is a “randomizing” effect, which makes the failures appear to lack any time dependency. However, if the failure modes were analyzed individually, the story would likely be very different (Figure 13). For certain, some failure modes would still be mathematically random, but many, and arguably most, would exhibit a time dependency. This kind of information would arm reliability engineers and managers with a powerful set of options for mitigating failure risk with a high degree of precision. Naturally, this ability depends upon the effective collection and subsequent analysis of field data.

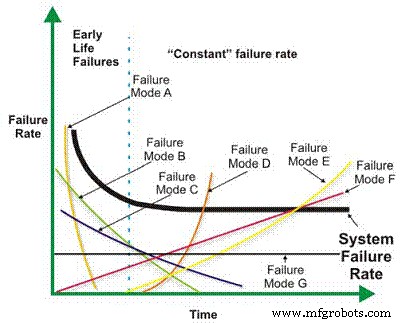
Figure 13. Good field data collection enables you to break the random trap.

This brief introduction to reliability engineering methods is intended to expose the otherwise uninitiated plant engineer to the world of quantitative reliability engineering. The subject is quite broad, however, and I’ve only touched on the major reliability methods that I believe are most applicable to the plant engineer. I encourage you to further investigate the field of reliability engineering methods, concentrating on the following topics, among others:

• More detailed understanding of the Weibull distribution and its applications

• More detailed understanding of the exponential distribution and its applications

• The Gaussian distribution and its applications

• The log-normal distribution and its applications

• Confidence intervals (binomial, chi-square/Poisson, etc.)

• Beta distribution and its applications

• Bayesian applications of reliability engineering methods

• Stress-strength interference analysis

• Testing options and their applicability to plant reliability engineering

• Reliability growth strategies and management

• More detailed understanding of field data collection.

Most important, spend time learning how to apply reliability engineering methods to plant reliability problems. If your interest in reliability engineering methods is high, I encourage you to pursue professional certification by the American Society for Quality as a reliability engineer (CRE).

References
Troyer, D. (2006) Strategic Plant Reliability Management Course Book, Noria Publishing, Tulsa, Oklahoma.

Bernowski, K (1997) “Safety in the Skies,” Quality Progress , January.

Dovich, R. (1990) Reliability Statistics, ASQ Quality Press, Milwaukee, WI.

Krishnamoorthi, K.S. (1992) Reliability Methods for Engineers, ASQ Quality Press , Milwaukee, WI.

MIL Standard 721

IEC Standard 300-3-3

DOE Standard NE-1004-92

Appendix:Select reliability engineering terms from MIL STD 721
Availability – A measure of the degree to which an item is in the operable and committable state at the start of the mission, when the mission is called for at an unknown state.

Capability – A measure of the ability of an item to achieve mission objectives given the conditions during the mission.

Dependability – A measure of the degree to which an item is operable and capable of performing its required function at any (random) time during a specified mission profile, given the availability at the start of the mission.

Failure – The event, or inoperable state, in which an item, or part of an item, does not, or would not, perform as previously specified.

Failure, dependent – Failure which is caused by the failure of an associated item(s). Not independent.

Failure, independent – Failure which occurs without being caused by the failure of any other item. Not dependent.

Failure mechanism – The physical, chemical, electrical, thermal or other process which results in failure.

Failure mode – The consequence of the mechanism through which the failure occurs, i.e. short, open, fracture, excessive wear.

Failure, random – Failure whose occurrence is predictable only in the probabilistic or statistical sense. This applies to all distributions.

Failure rate – The total number of failures within an item population, divided by the total number of life units expended by that population, during a particular measurement interval under stated conditions.

Maintainability – The measure of the ability of an item to be retained or restored to specified condition when maintenance is performed by personnel having specified skill levels, using prescribed procedures and resources, at each prescribed level of maintenance and repair.

Maintenance, corrective – All actions performed, as a result of failure, to restore an item to a specified condition. Corrective maintenance can include any or all of the following steps:localization, isolation, disassembly, interchange, reassembly, alignment and checkout.

Maintenance, preventive – All actions performed in an attempt to retain an item in a specified condition by providing systematic inspection, detection and prevention of incipient failures.

Mean time between failure (MTBF) – A basic measure of reliability for repairable items:the mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to failure (MTTF) – A basic measure of reliability for non-repairable items:The mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to repair (MTTR) – A basic measure of maintainability:the sum of corrective maintenance times at any specified level of repair, divided by the total number of failures within an item repaired at that level, during a particular interval under stated conditions.

Mission reliability – The ability of an item to perform its required functions for the duration of specified mission profile.

Reliability – (1) The duration or probability of failure-free performance under stated conditions. (2) The probability that an item can perform its intended function for a specified interval under stated conditions. For non-redundant items this is the equivalent to definition (1). For redundant items, this is the definition of mission reliability.