Apa itu Analisis Mesh :Prosedur dan Contohnya
Dalam domain elektronik, lebih penting untuk menganalisis bahkan rangkaian sederhana. Untuk analisis rangkaian sederhana, prinsip-prinsip seperti tegangan Kirchhoff dan hukum arus Kirchhoff digunakan. Sedangkan pada situasi rangkaian rumit yang memiliki beberapa sumber tegangan dan arus yang terkontrol, harus ada alat tambahan beserta hukum KVL dan KCL. Hanya dengan prinsip KVL dan KCL, analisisnya ternyata tidak akurat dan tidak reliabel juga. Jadi, untuk melakukan analisis yang tepat dan untuk mengetahui variabel di sirkuit tersebut, pendekatan seperti mesh dan nodal harus diterapkan. Dengan metode tersebut, variabel seperti arus dan tegangan dapat diketahui dengan mudah. Beri tahu kami dengan jelas tentang Analisis Mesh, Analisis super mesh di artikel ini.
Apa itu Analisis Mesh?
Mesh dianggap sebagai loop yang tidak memiliki loop lain di dalam sirkuit. Di sini, arus mesh digunakan sebagai variabel di tempat arus untuk mengetahui seluruh analisis rangkaian. Karena itu, teknik ini membutuhkan jumlah persamaan minimum untuk diselesaikan. Analisis mesh diimplementasikan di sirkuit menggunakan hukum tegangan Kirchhoff untuk mengetahui nilai arus yang tidak diketahui.
Ini juga disebut sebagai teknik loop arus mesh. Setelah itu, nilai tegangan juga dapat diketahui dengan penerapan hukum Ohm. Cabang dianggap sebagai jalur yang menghubungkan dua simpul dan termasuk dalam elemen rangkaian. Bila suatu mesh hanya terdiri dari satu cabang, maka arus cabang tersebut disebut sebagai arus mesh. Sedangkan jika mesh terdiri dari dua cabang, maka arus mesh dianggap sebagai jumlah atau selisih dari dua loop mesh ketika keduanya berada di jalur yang sama atau berlawanan.
Langkah
- Dalam mengetahui variabel-variabel rangkaian, ada prosedur yang harus diikuti untuk implementasi analisis mesh dan langkah-langkahnya dapat dijelaskan sebagai berikut:
- Pada tahap pertama, temukan mata jaring dan tandai arus mata rantai baik berlawanan arah jarum jam atau searah jarum jam.
- Lihat jumlah aliran arus yang mengalir melalui setiap elemen yang sesuai dengan arus mesh.
- Tuliskan semua persamaan mata jaring untuk mata jaring yang diamati. Persamaan mesh ditulis dengan menerapkan hukum Kirchhoff dan kemudian dengan menerapkan hukum Ohm
- Untuk mengetahui arus mesh, selesaikan persamaan mesh yang diamati sesuai langkah 3.
- Dengan ini, nilai aliran arus dan tegangan pada setiap elemen dalam rangkaian dapat diketahui dengan penerapan arus mesh.
Formulir Umum untuk Mengatur Persamaan dalam Analisis Mesh
Setelah identifikasi jerat di sirkuit, setiap terdiri dari satu persamaan. Persamaannya adalah total penurunan tegangan di seluruh loop arus mesh. Dalam kasus rangkaian, yang memiliki lebih dari tegangan dan arus, jatuh tegangan dianggap sebagai impedansi rangkaian yang dikalikan dengan arus mesh loop spesifik.
Ketika sumber tegangan ada di dalam loop, maka tegangan yang ada pada sumber dapat ditambahkan atau dikurangi berdasarkan kondisi apakah itu kehilangan tegangan atau peningkatan tegangan untuk mesh itu. Namun dalam kondisi ketika sumber arus tidak berada di antara mata jaring, maka arus mata jaring akan mempertimbangkan nilai negatif atau positif dari sumber berdasarkan arah sumber arus mata jaring.
Metode Mesh Saat Ini
Dengan rangkaian di bawah ini, analisis metode arus mesh dapat diketahui dengan mudah. Di sirkuit, arus loop I1 dan I2 diterapkan searah jarum jam
Bergantung pada arah arus loop, polaritas penurunan tegangan terjadi pada resistansi R1, R2, dan R3. Di sini, arus I1 dan I2 akan memiliki jalur aliran arus yang berlawanan karena resistor R2 berbagi kedua loop.
Jadi, kedua polaritas tegangan dapat diketahui. Sedangkan dalam skenario praktis, R2 dapat dikategorikan sebagai dua fase, tetapi arus loop terutama berlaku untuk aplikasi analisis. Tidak ada dampak pada polaritas sumber tegangan karena konstan.
Pada penerapan hukum tegangan Kirchhoff, dua persamaan di bawah ini dapat ditulis
R2(I1 – I2) + R1I1 =V1 – Berasal dari loop 1
R2(I2 – I1) + R1I2 =-V2 – Berasal dari loop 2
Suku-suku serupa dalam persamaan di atas digabungkan dan setelah diatur, suku-suku yang sama muncul pada posisi yang sama di setiap persamaan. Ketika arus loop diketahui, maka arus cabang dapat dievaluasi. Persamaan yang disusun ulang adalah:
I1(R1 + R2) – I2R2 =V1 – Untuk Loop 1 -I1R2 + (R2 – R3) I3 =-V2 – Untuk Loop 2
Analisis Mesh Menyelesaikan Masalah
Bagian ini menunjukkan contoh penyelesaian menemukan arus dalam rangkaian menggunakan metode arus mesh .
Pada rangkaian di bawah ini, tentukan besar tegangan yang melalui sumber arus 15 Amps dengan metode mesh analysis. Asalkan semua adalah sumber terkini
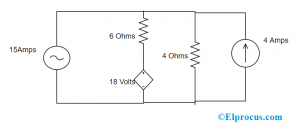 Analisis Jala Untuk Menemukan Tegangan
Analisis Jala Untuk Menemukan Tegangan
Sesuai rangkaian, ada kemungkinan mengubah sumber tegangan menjadi arus menggunakan resistansi paralel. Untuk melakukan ini, resistor ditempatkan dalam hubungan seri dengan sumber tegangan dan resistor harus memiliki nilai yang sama dengan sumber tegangan dan tegangannya
Vs =IsRs =4 * 4 =16V
Cari tahu arus cabang (I1 dan I2) untuk loop dan tentukan arah aliran arus di kedua loop.
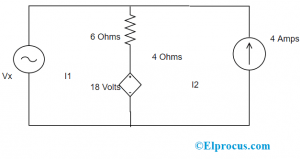 Menetapkan Cabang Arus
Menetapkan Cabang Arus
Kemudian, untuk setiap mesh (loop), terapkan hukum KVL
Jala – 1
Vx – (I1 – I2) – 18 =0
Di sini, I1 =15
Jadi, Vx + (6 * I2) =90
Jala – 2
18 – 6 (I2 – I1) – 4 * I2 – 16 =0
I2 =78/10
=7,8 Amps
Sesuai dengan persamaan Mesh-1
Vx =90 – 44,4
Vx =45,6 V
Ini adalah contoh penyelesaian dari Memecahkan Dua Mesh menggunakan Analisis Arus Mesh
Di sini, kita perlu mencari tahu tegangan dan arus cabang. Perhatikan rangkaian di bawah ini.
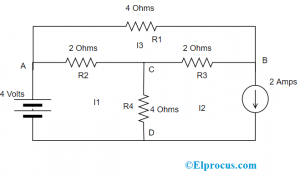 Arus Jala Metode Di Tiga Jerat
Arus Jala Metode Di Tiga Jerat
Dengan penerapan hukum KVL pada loop pertama, kita peroleh
V1 – R2 (I1 – I3) – R4 (I1 – I2) =0
4 – 2(I1) – 2(I3) – 4 (I1) – 4(I2) =0
-2(I3) – 6 (I1) =4
Pada penerapan hukum KVL pada mesh kedua, kita dapatkan
-Vc – R4 (I2 – I1) – R3 (I2 – I3) =0
-Vc =-4(I1) + 6(I2) – 2 (I3) =0
Karena I2 =-2A, kita peroleh
-Vc =-4(I1) -12 – 2 (I3) =0
Pada penerapan hukum KVL pada mesh ketiga, kita mendapatkan
-R1(I3) – R3(I3 – I2) – R2 (I3 – I1) =0
Mengganti I2 =-2A
2(I1) – 8(I3) =0
Dengan memecahkan persamaan mesh pertama dan ketiga, kita mendapatkan
I1 =4,46 dan I3 =-0,615
Jadi, Vc =28.61V
Dan arus cabang adalah
Iac =I1 – I3
Iac =5,075 amp
Ini adalah contoh penyelesaian dari menyelesaikan tiga mesh menggunakan Analisis Arus Mesh
Ini adalah contoh contoh yang diselesaikan melalui analisis mesh. Analisis menyeluruh dari konsep ini memungkinkan kita untuk memecahkan sirkuit yang kompleks juga.
Analisis Jala Super
Untuk analisis sirkuit besar dan kompleks, analisis mesh super berfungsi sebagai pendekatan terbaik daripada analisis Mesh dimana karena dalam mesh super akan ada dua mesh yang berbagi komponen yang sama sebagai sumber arus.
Teknik yang sama diikuti untuk analisis rangkaian supernode sebagai alternatif untuk analisis rangkaian node karena metode ini merampingkan rangkaian kompleks tersebut dengan menutup elemen tegangan dan meminimalkan jumlah node referensi untuk setiap sumber tegangan. Dalam analisis super mesh, sumber arus terletak di bagian dalam super mesh, sehingga seseorang dapat meminimalkan mesh satu per satu untuk setiap sumber arus yang ada.
Ketika sumber arus ada pada izin sirkuit, maka jala tunggal mungkin tidak dipertimbangkan. Di sisi lain, KVL diimplementasikan hanya untuk jerat di sirkuit listrik yang dimodifikasi.
Mari kita pertimbangkan contoh analisis mesh super untuk pemahaman yang lebih baik.
Dengan menggunakan analisis super mesh, cari tahu nilai V3, i1, i2, dan i3 untuk rangkaian di bawah ini?
Pada penerapan KVL ke Mesh-1, kita mendapatkan
10i1 + 80(i1 – i2) + 30 (i1 – i3) =80
Kami mendapatkan 60i1 – 20i2 – 30i3 =80
Dengan penerapan teknik super mesh pada Mesh 2 dan Mesh 3, kita mendapatkan
30 =40i3+ 30 (i3 – i1) + 20(i2 – i1)
70i3 – 50i1+ 20i2 =30
Sumber arus individu yang ada di mesh super sesuai dengan arus mesh yang diharapkan yaitu
15ix =i3 – i2
I3 =15ix + i2
Dengan menyelesaikan ketiga persamaan di atas, kita mendapatkan
i1 =0.58 Amps, i2 =-6.16 Amps dan i3 =2.6 Amps
Untuk mencari V3, kita punya v3 =i3 * R3, Jadi
V3 =2,6 * 40 =104V
Penggunaan Analisis Mesh
Penggunaan utama dari analisis mesh adalah untuk menyelesaikan rangkaian planar untuk mengetahui nilai arus pada setiap posisi baik dalam rangkaian listrik sederhana maupun rumit
Penggunaan lainnya adalah komputasi normal untuk menyelesaikan persamaan sulit dan membutuhkan lebih banyak rumus matematika, sedangkan melalui analisis mesh, komputasi yang lebih sedikit sudah cukup.
Penggunaan lain dari analisis Mesh Current adalah jembatan batu gandum yang tidak seimbang. Untuk mengetahuinya, perhatikan contoh di bawah ini
Karena proporsi resistor, R1/R4 dan R2/R5 tidak sama, kita dapat memahami bahwa akan ada sejumlah tegangan dan arus yang mengalir di R3. Seperti yang kita ketahui bahwa menyelesaikan jenis rangkaian ini rumit dengan pendekatan teknik seri-paralel umum, kita memerlukan pendekatan lain untuk menyelesaikannya.
Jadi, sehubungan dengan itu, kita dapat menggunakan metode arus cabang, tetapi metode ini membutuhkan enam arus dari Ia ke If yang mengarah untuk bekerja pada sejumlah persamaan. Jadi, kerumitan ini dapat dengan mudah dikurangi melalui metode Mesh saat ini di mana ini hanya membutuhkan beberapa variabel.






