Dua Teknik untuk Linierisasi Jembatan Sensor Resistif
Mengukur perubahan resistansi yang sangat kecil pada sensor resistif bisa menjadi tugas yang menakutkan. Berikut adalah dua metode perangkat keras untuk menghilangkan kesalahan non-linier jembatan.
Resistansi sensor resistif tergantung pada variabel fisik seperti suhu atau gaya. Persentase perubahan resistansi perangkat ini biasanya kecil. Misalnya, perubahan total resistansi pengukur regangan mungkin kurang dari 1% di seluruh rentang operasinya.
Membedakan nilai-nilai kecil ini mengamanatkan sirkuit pengukuran yang sangat akurat. Sirkuit jembatan memungkinkan kita untuk lebih mudah melakukan pengukuran yang akurat ini. Namun, output dari rangkaian jembatan mungkin memiliki hubungan non-linier dengan variabel fisik yang diukur bahkan jika kita menggunakan sensor linier.
Dalam kasus ini, kita dapat menggunakan teknik perangkat lunak atau perangkat keras untuk menghilangkan kesalahan non-linier jembatan. Dalam artikel ini, kita akan melihat dua teknik berbeda dari linearisasi jembatan sensor resistif.
Non-linearitas Jembatan Sensor Resistif
Pertimbangkan sensor tekanan resistif dengan respons linier berikut:
\[R_{sensor} =R_0 + Mx\]
di mana R0 adalah resistansi awal sensor pada tekanan nol, x adalah nilai besaran ukur (tekanan), dan M adalah kemiringan respons sensor. Untuk membuat persamaan masa depan kita lebih sederhana, mari kita asumsikan bahwa nilai M sama dengan nilai resistansi awal sensor (R0 ) dan karenanya, respons sensor adalah \[R_0(1+x)\].
Biasanya, persentase perubahan resistansi sensor resistif kecil dan kita perlu menggunakan rangkaian jembatan untuk lebih mudah melakukan pengukuran yang akurat. Konfigurasi jembatan umum untuk sensor ini digambarkan pada Gambar 1.
Gambar 1. Konfigurasi jembatan umum dari sensor resistif
Perhatikan bahwa tiga resistor jembatan lainnya memiliki resistansi R0 . Pilihan resistor jembatan ini memaksimalkan sensitivitas output (Vkeluar ) terhadap perubahan resistansi sensor. Persamaan output dapat diperoleh sebagai:
\[V_{out} =V_A - V_B =V_r\left(\frac{R_0(1+x)}{R_0+R_0(1+x)} - \frac {1}{2}\kanan)\]
Ini disederhanakan menjadi:
\[V_{out} =V_r\left(\frac{x}{2(2+x)}\right)\]
Persamaan 1.
Seperti yang Anda lihat, hubungan antara keluaran jembatan dan perubahan nilai resistansi (x) tidak linier. Dengan \[x\ll2\], persamaan di atas dapat didekati dengan hubungan linier berikut:
\[V_{out} \kira-kira V_r\left(\frac{x}{4}\right)\]
Persamaan 2.
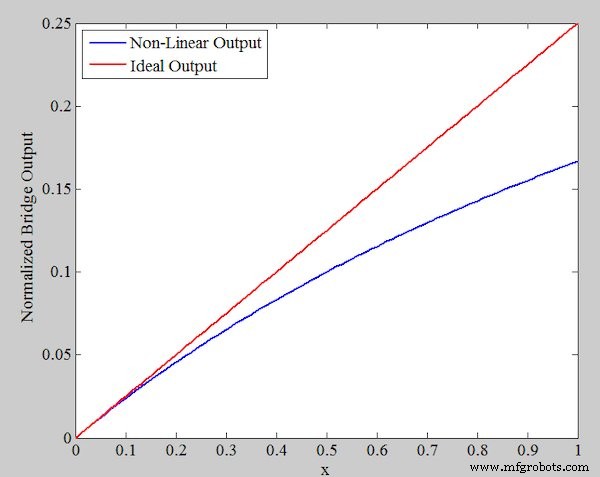
Gambar 2 menggambarkan keluaran jembatan yang dinormalisasi \[\frac{V_{out}}{V_r}\] untuk kasus aktual (Persamaan 1) dan keluaran ideal (Persamaan 2).

Gambar 2. Keluaran non-linier (biru) dan ideal (merah) dari Persamaan 1 dan 2
Seperti yang diharapkan, deviasi dari respon linier meningkat dengan x.
Berapa Banyak Kesalahan Non-linier yang Akan Terjadi?
Mari kita hitung kesalahan non-linier dari rangkaian jembatan di atas. Kita dapat menulis ulang Persamaan 1 sebagai:
\[V_{out} =V_r \left(\frac{x}{4}\right) \left(\frac{1}{1+ \frac{x} {2}}\kanan)\]
Dengan asumsi bahwa \[\frac{x}{2} <<1\], kita dapat menggunakan teorema Taylor untuk mendapatkan aproksimasi dari fungsi di atas sebagai:
\[V_{out} =V_r\left(\frac{x}{4}\right)\left(1 - \frac{x}{2}\right) \]
Membandingkan hasil ini dengan Persamaan 2, kita dapat menghitung besarnya kesalahan sebagai:
\[E_{Non-Linearity} =V_r\left(\frac{x}{4}\right)\left(\frac{x}{2}\right) \]
Membagi ini dengan nilai ideal yang diharapkan yang diberikan oleh Persamaan 2, kita dapat memperoleh persentase kesalahan linieritas titik akhir untuk perubahan resistansi (x):
\[Persentase~Kesalahan =\frac{x}{2} \times 100\%\]
Contoh Menghitung Error Non-Linearitas
Pertimbangkan sebuah sensor dengan respons \[R_{sensor} =R_0(1+x)\]. Asumsikan bahwa \[R_0 =100~\Omega\] dan nilai maksimum x di seluruh rentang operasi adalah 0,01. Persentase kesalahan linearitas maksimum adalah:
\[Persentase~Error =\left(\frac{0.01}{2}\right) \times 100\% =0.5\%\]
Perhatikan bahwa meskipun kita mungkin dapat menggunakan perangkat lunak untuk menghilangkan kesalahan linearitas sensor, memiliki respons linier diinginkan karena meningkatkan presisi pengukuran dan memfasilitasi kalibrasi sistem. Ada topologi sirkuit yang berbeda yang dapat digunakan untuk linierisasi sirkuit jembatan.
Di sisa artikel ini, kita akan membahas dua teknik linierisasi jembatan yang berbeda.
Metode 1:Membuat Tegangan Proporsional dengan Perubahan Resistansi (x)
Teknik linierisasi pertama yang akan kita bahas dalam artikel ini ditunjukkan pada Gambar 3. Pertama-tama mari kita periksa ide dasar teknik ini dan kemudian lihat bagaimana rangkaian pada Gambar 3 mengimplementasikan ide ini.
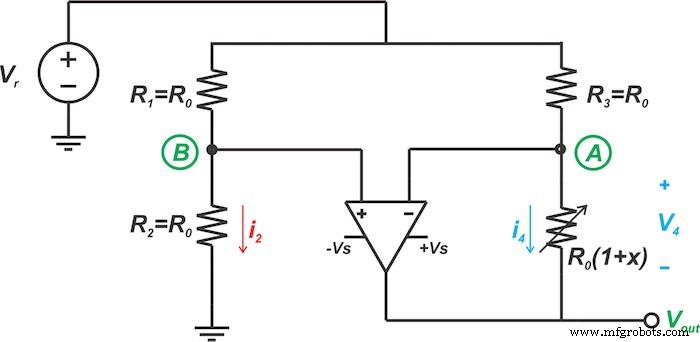
Gambar 3. Salah satu jenis sirkuit untuk linierisasi jembatan sensor resistif
Gambar 4 menunjukkan penggambaran arus tetap \[I_{Ref}\] dipaksa untuk mengalir melalui sensor linier kami.
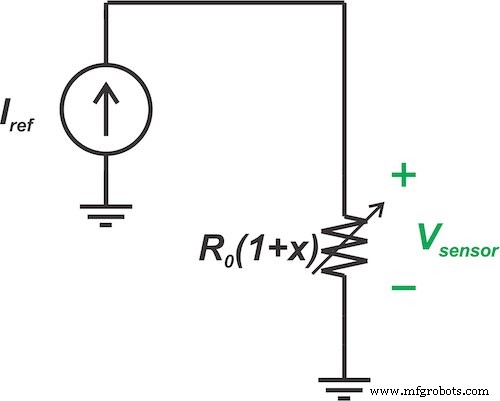
Gambar 4. Arus tetap (IRef ) dipaksa melalui sensor linier
Dalam skenario ini, tegangan yang dihasilkan melintasi sensor adalah:
\[V_{sensor} =I_{Ref} \times R_0(1 + x)\]
yang dapat diatur ulang sebagai:
\[V_{sensor} =R_0 \times I_{Ref} + R_0 \times I_{Ref} \times x\]
Sedangkan suku pertama adalah nilai konstan, suku kedua sebanding dengan perubahan resistansi sensor (x). Jika kita dapat menghilangkan suku konstan, kita akan memiliki tegangan yang memiliki hubungan linier dengan x.
Implementasi Sirkuit
Rangkaian pada Gambar 3 menggunakan ide di atas untuk linierisasi rangkaian jembatan. Karena input op-amp idealnya tidak menarik arus, tegangan pada simpul B akan memiliki nilai konstan:
\[v_B =\frac{R_0}{R_0 + R_0}V_r =\frac{V_r}{2}\]
Umpan balik negatif bersama dengan penguatan tinggi op-amp akan memaksa input op-amp pembalik dan non-pembalik memiliki tegangan yang sama:
\[v_A =v_B =\frac{V_r}{2}\]
Karena kedua ujung R3 berada pada potensial konstan, arus konstan akan mengalir melaluinya. Dengan kata lain, op-amp membuat R3 bertindak sebagai sumber arus yang memaksa arus konstan \[\frac{V_r}{2R_0}\] ke dalam sensor. Oleh karena itu, tegangan melintasi sensor akan menjadi:
\[V_4 =\frac{V_r}{2R_0} \times R_0(1 + x) =\frac{V_r}{2} + \frac{V_r}{2} x\]
Suku pertama adalah nilai konstanta yang harus dihilangkan dari Vkeluar persamaan. Suku kedua sebanding dengan perubahan resistansi sensor (x) dan akan muncul dalam persamaan keluaran. Menerapkan hukum tegangan Kirchhoff, kami menemukan Vkeluar sebagai:
\[V_{out} =-V_4 + V_A =- \left(\frac{V_r}{2} + \frac{V_r}{2}x\right) + V_A\]
Oleh karena itu, kita hanya perlu VA sama dengan \[\frac{V_r}{2}\]. Ini sudah terpenuhi, yang mengarah ke:
\[V_{out} =-\frac{V_r}{2}x\]
Oleh karena itu, output memiliki hubungan linier dengan x.
Metode 2:Membuat Proporsional Arus terhadap Perubahan Resistansi (x)
Teknik linierisasi jembatan kedua yang akan kita bahas dalam artikel ini ditunjukkan pada Gambar 5.
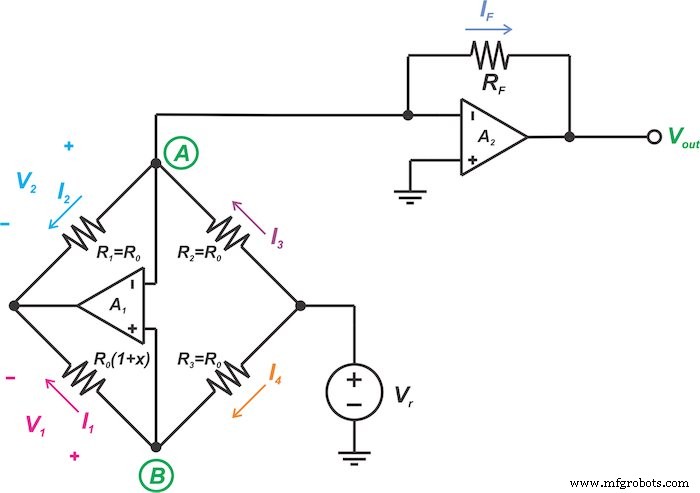
Gambar 5. Sirkuit lain untuk linierisasi analog jembatan sensor resistif
Mari kita lihat kembali ide dasar dari teknik ini dan kemudian periksa implementasi rangkaiannya.
Teknik linearisasi kedua ini diilustrasikan pada Gambar 6.
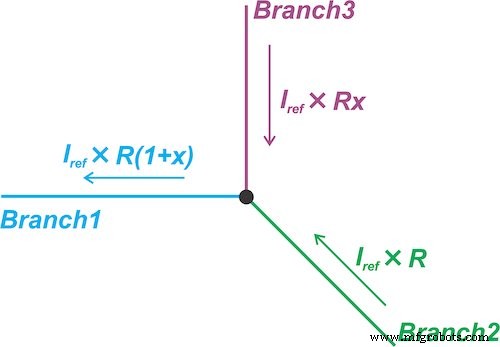
Gambar 6. Teknik linierisasi yang memaksa arus melalui cabang rangkaian sebanding dengan resistansi sensor
Ini memaksa arus melalui cabang sirkuit (Cabang 1) sebanding dengan resistansi sensor:
\[I_1 =I_{Ref} \times R_0(1 + x)\]
di mana sayaRef adalah nilai konstan. Kemudian, ia melakukan pengurangan domain saat ini untuk menghilangkan suku konstan \[I_{Ref} \times R_0\]. Untuk tujuan ini, arus yang melalui Cabang 2 diatur menjadi \[I_{Ref} \times R_0\]. Oleh karena itu, arus yang melalui Cabang 3 akan menjadi \[I_{Ref} \times R_0x\]— sebanding dengan perubahan resistansi sensor (x).
Implementasi Sirkuit
Mari kita lihat bagaimana rangkaian pada Gambar 5 mengimplementasikan ide di atas. Sekali lagi, umpan balik negatif bersama dengan penguatan tinggi dari op-amp akan memaksa input pembalik dan non-pembalik dari kedua op-amp (keduanya A1 dan A2 ) memiliki tegangan yang sama:
\[v_A =v_B =0\]
Persamaan 3.
Oleh karena itu, kami memiliki V1 =V2 yang mengarah ke
\[R_0 (1 + x) \times I_1 =R_0 \times I_2\]
Ini disederhanakan menjadi:
\[I_2 =I_1 + I_1 \times x\]
Persamaan 4.
Kita tahu bahwa Saya1 =I4 dan, dengan mempertimbangkan Persamaan 3, kita mendapatkan:
\[I_1 =I_4 =\frac{V_r - v_A}{R_0} =\frac{V_r}{R_0}\]
Substitusikan ini ke dalam Persamaan 4, kita peroleh:
\[I_2 =\frac{V_r}{R_0} + \frac{V_r}{R_0} \times x\]
Oleh karena itu, Saya2 adalah jumlah dari suatu nilai konstanta dan suatu suku yang sebanding dengan x. Kita hanya perlu menggunakan hukum Kirchhoff saat ini untuk menghilangkan suku konstan dalam persamaan arus keluaran. Arus melalui R2 sumber arus sama dengan \[\frac{V_r}{R_0}\] ke simpul A, yang mengarah ke:
\[I_F =-\frac{V_r}{R_0} \times x\]
Oleh karena itu, kita memperoleh:
\[V_{out} =V_r \times \frac{R_F}{R_0} \times x\]
Rangkaian pada Gambar 5 membutuhkan op-amp tambahan dibandingkan dengan teknik pertama. Namun, dengan dua solusi op-amp, kita dapat mengatur penguatan secara sewenang-wenang dengan memilih rasio \[\frac{R_F}{R_0}\].
Untuk melihat daftar lengkap artikel saya, silakan kunjungi halaman ini.








