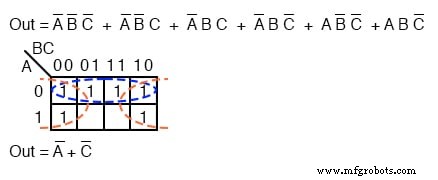Contoh penyederhanaan logika yang telah kita lakukan sejauh ini dapat dilakukan dengan aljabar Boolean dengan cepat. Masalah penyederhanaan logika dunia nyata membutuhkan peta Karnaugh yang lebih besar sehingga kami dapat melakukan pekerjaan yang serius.
Kami akan mengerjakan beberapa contoh yang dibuat-buat di bagian ini, meninggalkan sebagian besar aplikasi dunia nyata untuk bab Logika Kombinatorial. Dengan dibuat-buat, yang kami maksud adalah contoh yang menggambarkan teknik.
Pendekatan ini akan mengembangkan alat yang kita butuhkan untuk transisi ke aplikasi yang lebih kompleks di bab Logika Kombinatorial.
Kami menunjukkan peta Karnaugh yang kami kembangkan sebelumnya. Kami akan menggunakan formulir di sebelah kanan.
Perhatikan urutan angka di bagian atas peta. Itu bukan dalam urutan biner yang akan menjadi 00, 01, 10, 11 . Ini 00, 01, 11 10 , yang merupakan urutan kode Gray. Urutan kode abu-abu hanya mengubah satu bit biner saat kita berpindah dari satu angka ke angka berikutnya dalam urutan, tidak seperti biner.
Itu berarti bahwa sel-sel yang berdekatan hanya akan bervariasi satu bit, atau variabel Boolean. Inilah yang kita perlukan untuk mengatur output dari fungsi logika sehingga kita dapat melihat kesamaan.
Selain itu, judul kolom dan baris harus dalam urutan kode Gray, atau peta tidak akan berfungsi sebagai peta Karnaugh. Sel yang berbagi variabel Boolean umum tidak akan lagi berdekatan, atau menunjukkan pola visual.
Sel yang berdekatan bervariasi hanya satu bit karena urutan kode Gray hanya bervariasi satu bit.
Jika kita membuat sketsa peta Karnaugh kita sendiri, kita perlu membuat kode Gray untuk peta ukuran apa pun yang mungkin kita gunakan. Beginilah cara kami menghasilkan kode Gray dengan ukuran berapa pun.
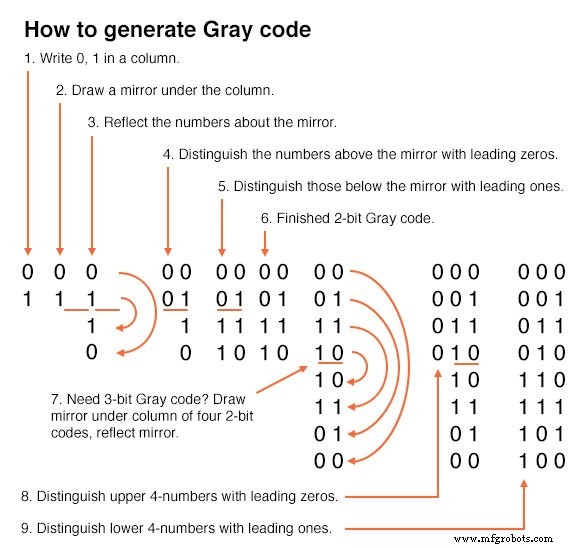
Perhatikan bahwa urutan kode Gray, kanan atas, hanya bervariasi satu bit saat kita turun daftar, atau bawah ke atas daftar. Properti kode Gray ini sering berguna untuk elektronik digital secara umum. Secara khusus, ini berlaku untuk peta Karnaugh.
Mari kita beralih ke beberapa contoh penyederhanaan dengan peta Karnaugh 3-variabel. Kami menunjukkan cara memetakan istilah produk dari logika yang tidak disederhanakan ke K-map.
Kami mengilustrasikan cara mengidentifikasi grup sel yang berdekatan yang mengarah ke penyederhanaan Sum-of-Products dari logika digital.
Di atas kita, tempatkan 1 di K-map untuk setiap istilah produk, identifikasi kelompok dua, lalu tulis p-term (istilah produk) untuk satu-satunya grup sebagai hasil sederhana kami.
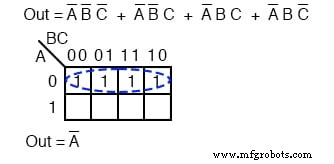
Memetakan empat istilah produk di atas menghasilkan sekelompok empat yang dicakup oleh Boolean A'
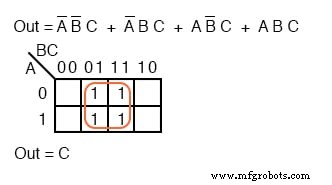
Memetakan empat suku-p menghasilkan kelompok empat, yang dicakup oleh satu variabel C .
Setelah memetakan enam suku-p di atas, identifikasi kelompok empat atas, ambil dua sel bawah sebagai kelompok empat dengan berbagi dua dengan dua lagi dari kelompok lain. Menutupi keduanya dengan kelompok empat memberikan hasil yang lebih sederhana.
Karena ada dua grup, akan ada dua suku-p dalam hasil Jumlah Produk A’+B
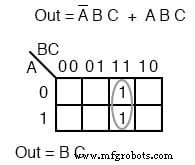
Dua suku produk di atas membentuk satu kelompok yang terdiri dari dua dan disederhanakan menjadi BC
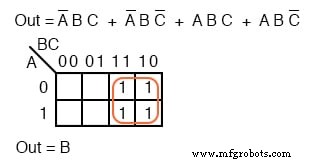
Memetakan empat suku-p menghasilkan satu kelompok empat, yaitu B
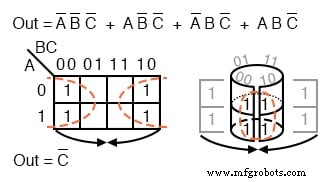
Memetakan empat suku-p di atas menghasilkan kelompok yang terdiri dari empat orang. Visualisasikan kelompok empat dengan menggulung ujung peta untuk membentuk silinder, lalu sel-selnya berdekatan. Kami biasanya menandai kelompok empat seperti kiri di atas.
Dari variabel A, B, C, ada variabel umum:C’. C' adalah 0 keseluruhan empat sel. Hasil akhirnya adalah C’
. 
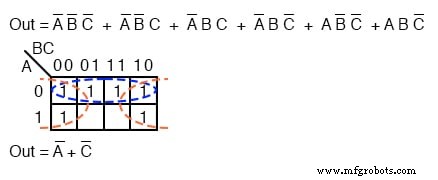
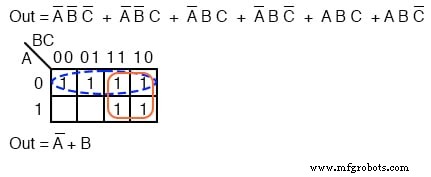
Keenam sel di atas dari persamaan yang tidak disederhanakan dapat diatur menjadi dua kelompok yang terdiri dari empat. Kedua grup ini seharusnya memberi kita dua suku-p dalam hasil sederhana dari A’ + C’ .
Di bawah ini, kami meninjau kembali insinerator limbah beracun dari bab aljabar Boolean. Lihat bab aljabar Boolean untuk detail tentang contoh ini. Kami akan menyederhanakan logika menggunakan peta Karnaugh.
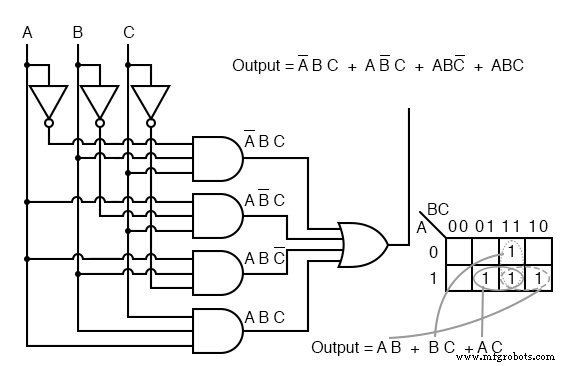
Persamaan Boolean untuk output memiliki empat suku produk. Petakan empat 1 yang sesuai dengan suku-p. Membentuk kelompok sel, kami memiliki tiga kelompok dua. Akan ada tiga suku-p dalam hasil yang disederhanakan, satu untuk setiap grup. Lihat Mengubah Tabel Kebenaran menjadi Ekspresi Boolean dari bab 7 untuk diagram gerbang hasil, yang direproduksi di bawah ini.
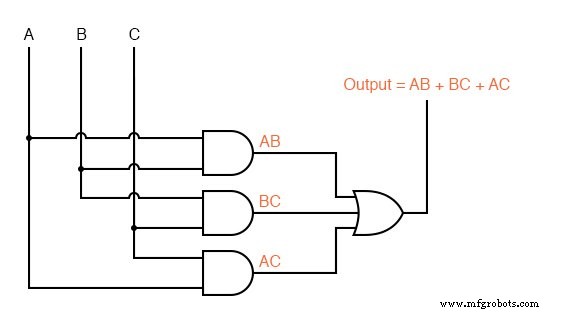
Di bawah ini kami mengulangi penyederhanaan aljabar Boolean dari insinerator limbah beracun sebagai perbandingan.
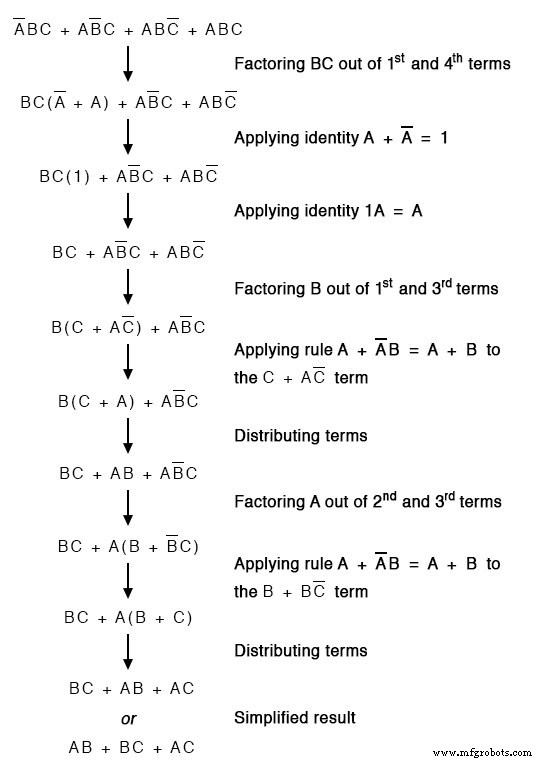
Di bawah ini kami ulangi solusi peta Karnaugh insinerator limbah beracun untuk perbandingan dengan penyederhanaan aljabar Boolean di atas. Kasus ini menggambarkan mengapa peta Karnaugh banyak digunakan untuk penyederhanaan logika.
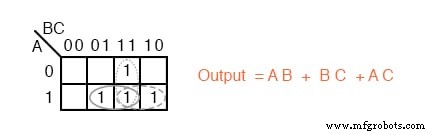
Metode peta Karnaugh jelas terlihat lebih mudah daripada halaman aljabar Boolean sebelumnya.
LEMBAR KERJA TERKAIT:
Lembar Kerja Pemetaan Karnaugh
Teknologi Industri
Dalam artikel ini Anda dapat mempelajari bagaimana membuat rangkaian listrik untuk manufaktur dapat menjadi sederhana dan intuitif di dalam E3.series. Harness dapat memiliki aplikasi yang berbeda seperti otomasi industri dan untuk industri otomotif. Lihat artikel selengkapnya. Pembuatan harness
Di masa lalu, ketika memprogram geometri berbentuk persegi panjang pada kontrol Hurco, di mana keempat sudutnya tidak persegi atau tidak semuanya memiliki jari-jari ukuran yang sama, fitur tersebut perlu diprogram menggunakan blok data Garis Penggilingan &Busur. Namun, dengan diperkenalkannya perang
Selama beberapa dekade, produk menjadi lebih kecil dan lebih ramping. Akibatnya, cetakan mikro muncul sebagai solusi bagi perancang produk untuk merancang produk dan komponen kecil agar sesuai dengan teknologi modern saat ini. Dalam postingan ini, kami akan mengungkap pencetakan mikro dan manfaat pe
Salah satu pertanyaan paling umum yang kami dapatkan dari pelanggan yang ingin membuat suku cadang yang sudah ada dengan manufaktur aditif adalah, “Apa bahan aditif sebanding yang dapat saya gunakan untuk memastikan suku cadang saya akan menjadi sama?” Dalam beberapa kasus, pemilihan material bisa
