Rangkaian Pembagi Arus dan Rumus Pembagi Arus

Rangkaian paralel sering disebut pembagi arus karena kemampuannya untuk membagi—atau membagi—jumlah arus menjadi bagian-bagian pecahan.

Untuk memahami apa artinya ini, pertama-tama mari kita menganalisis rangkaian paralel sederhana, menentukan arus cabang melalui resistor individu

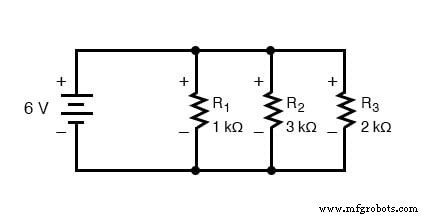
Mengetahui bahwa tegangan di semua komponen dalam rangkaian paralel adalah sama, kita dapat mengisi tabel tegangan/arus/hambatan kita dengan 6 volt di baris atas:

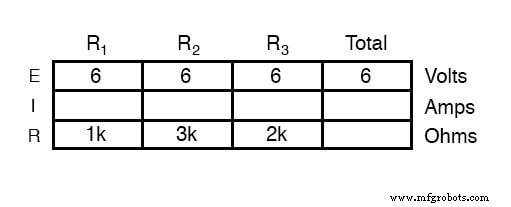
Menggunakan Hukum Ohm (I=E/R) kita dapat menghitung setiap arus cabang:

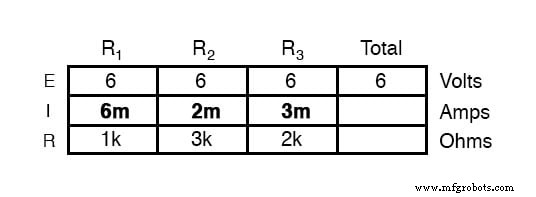
Mengetahui bahwa arus cabang dijumlahkan dalam rangkaian paralel sama dengan arus total, kita dapat memperoleh arus total dengan menjumlahkan 6 mA, 2 mA, dan 3 mA:

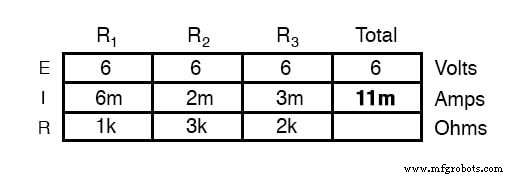
Langkah terakhir, tentu saja, adalah menghitung hambatan total. Ini dapat dilakukan dengan Hukum Ohm (R=E/I) di kolom “total”, atau dengan rumus resistansi paralel dari resistansi individu. Bagaimanapun, kita akan mendapatkan jawaban yang sama:

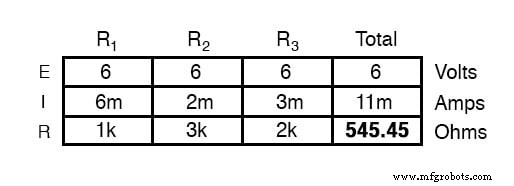
Sekali lagi, harus jelas bahwa arus yang melalui setiap resistor terkait dengan resistansinya, mengingat tegangan pada semua resistor adalah sama. Alih-alih berbanding lurus, hubungan di sini adalah hubungan berbanding terbalik. Misalnya, arus melalui R₁ dua kali lebih besar dari arus yang melalui R₃ , yang memiliki dua kali resistansi R₁ .

Jika kita mengubah tegangan suplai rangkaian ini, kita menemukan bahwa (kejutan!) rasio proporsional ini tidak berubah:

Menghitung Rasio Saat Ini

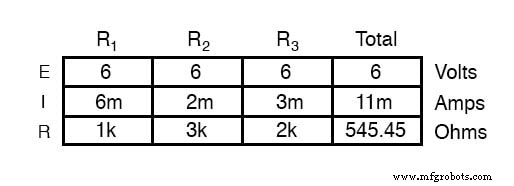
Arus melalui R₁ masih persis dua kali lipat dari R₃ , terlepas dari kenyataan bahwa tegangan sumber telah berubah. Proporsionalitas antara arus cabang yang berbeda benar-benar merupakan fungsi dari resistansi.

Juga mengingatkan pada pembagi tegangan adalah kenyataan bahwa arus cabang adalah proporsi tetap dari arus total. Meskipun tegangan suplai meningkat empat kali lipat, rasio antara arus cabang dan arus total tetap tidak berubah:

Sekarang kita dapat melihat sendiri poin yang kita buat di awal halaman ini:Rangkaian paralel sering disebut pembagi arus karena kemampuannya untuk membagi—atau membagi—jumlah arus menjadi bagian-bagian pecahan.

Rumus Pembagi Saat Ini

Dengan sedikit aljabar, kita dapat memperoleh rumus untuk menentukan arus resistor paralel yang diberikan tidak lebih dari arus total, resistansi individu, dan resistansi total:

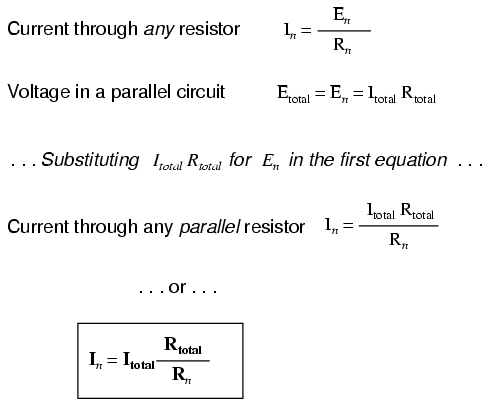
Rasio resistansi total terhadap resistansi individu adalah rasio yang sama dengan arus individu (cabang) terhadap arus total. Ini dikenal sebagai rumus pembagi arus , dan merupakan metode jalan pintas untuk menentukan arus cabang pada rangkaian paralel ketika arus total diketahui.

Contoh Rumus Pembagi Saat Ini

Menggunakan rangkaian paralel asli sebagai contoh, kita dapat menghitung ulang arus cabang menggunakan rumus ini, jika kita mulai dengan mengetahui arus total dan hambatan total:

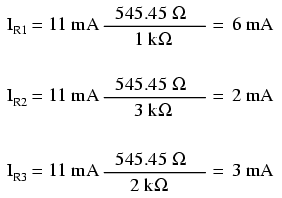
Jika Anda meluangkan waktu untuk membandingkan dua formula pembagi, Anda akan melihat bahwa keduanya sangat mirip. Namun, perhatikan bahwa rasio dalam rumus pembagi tegangan adalah R_n (resistensi individu) dibagi dengan R_Total , dan bagaimana rasio dalam rumus pembagi saat ini adalah R_Total dibagi dengan R_n :

Rumus Pembagi Arus vs. Rumus Pembagi Tegangan

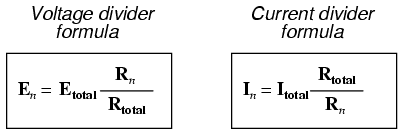
Sangat mudah untuk mengacaukan kedua persamaan ini, membuat rasio resistansi mundur. Salah satu cara untuk membantu mengingat bentuk yang tepat adalah dengan mengingat bahwa kedua rasio dalam persamaan pembagi tegangan dan arus harus kurang dari satu. Bagaimanapun, ini adalah pembagi persamaan, bukan pengganda persamaan! Jika pecahan terbalik, rasionya akan lebih besar dari satu, yang tidak benar.

Mengetahui bahwa resistansi total dalam rangkaian seri (pembagi tegangan) selalu lebih besar daripada resistansi individu mana pun, kita tahu bahwa fraksi untuk rumus itu harus R_n lebih dari R_Total . Sebaliknya, mengetahui bahwa hambatan total dalam rangkaian paralel (pembagi arus) selalu lebih kecil daripada hambatan individu mana pun, kita tahu bahwa pecahan untuk rumus tersebut harus R_Total lebih dari R_n .

Aplikasi Contoh Rangkaian Pembagi Arus:Rangkaian Meter Listrik

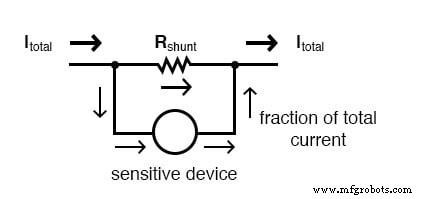
Sirkuit pembagi arus juga menemukan aplikasi di sirkuit meteran listrik, di mana sebagian kecil dari arus terukur diinginkan untuk disalurkan melalui perangkat deteksi sensitif. Menggunakan rumus pembagi arus, resistor shunt yang tepat dapat diukur dengan proporsi jumlah arus yang tepat untuk perangkat dalam contoh tertentu:

TINJAUAN:

• Proporsi rangkaian paralel, atau “membagi”, arus rangkaian total di antara masing-masing arus cabang, proporsinya sangat bergantung pada resistansi:I_n =I_Total (R_Total / R_n )

LEMBAR KERJA TERKAIT:

• Lembar Kerja Sirkuit Pembagi Saat Ini