Teorema Thevenin

Teorema Thevenin menyatakan bahwa adalah mungkin untuk menyederhanakan rangkaian linier apa pun, betapapun rumitnya, menjadi rangkaian ekivalen dengan hanya satu sumber tegangan dan resistansi seri yang terhubung ke beban. Kualifikasi "linier" identik dengan yang ditemukan dalam Teorema Superposisi, di mana semua persamaan yang mendasarinya harus linier (tidak ada eksponen atau akar). Jika kita berurusan dengan komponen pasif (seperti resistor, dan kemudian, induktor dan kapasitor), ini benar. Namun, ada beberapa komponen (terutama komponen pelepasan gas dan semikonduktor tertentu) yang nonlinier:yaitu, penentangannya terhadap perubahan saat ini. dengan tegangan dan/atau arus. Dengan demikian, kami akan menyebut sirkuit yang berisi jenis komponen ini, sirkuit nonlinier .

Teorema Thevenin dalam Sistem Tenaga

Teorema Thevenin sangat berguna dalam menganalisis sistem tenaga dan sirkuit lain di mana satu resistor tertentu di sirkuit (disebut resistor "beban") dapat berubah, dan perhitungan ulang sirkuit diperlukan dengan setiap nilai percobaan resistansi beban, untuk tentukan tegangan yang melewatinya dan arus yang melaluinya. Mari kita lihat lagi rangkaian contoh kita:

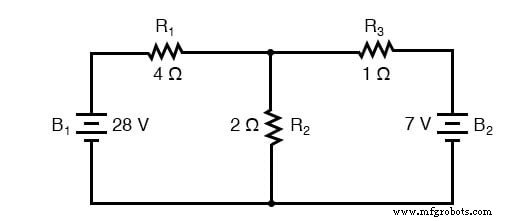
Misalkan kita memutuskan untuk menunjuk R₂ sebagai resistor "beban" di sirkuit ini. Kami telah memiliki empat metode analisis (Arus Cabang, Arus Mesh, Teorema Millman, dan Teorema Superposisi) untuk digunakan dalam menentukan tegangan melintasi R₂ dan arus melalui R₂ , tetapi masing-masing metode ini memakan waktu. Bayangkan mengulangi salah satu metode ini berulang-ulang untuk menemukan apa yang akan terjadi jika resistansi beban berubah (mengubah resistansi beban sangat umum dalam sistem tenaga, karena banyak beban dinyalakan dan dimatikan sesuai kebutuhan. resistansi total dari koneksi paralelnya berubah tergantung pada berapa banyak yang terhubung pada suatu waktu). Ini berpotensi melibatkan banyak pekerjaan!

Rangkaian Setara Thevenin

Teorema Thevenin membuatnya mudah dengan menghilangkan sementara resistansi beban dari rangkaian asli dan mengurangi apa yang tersisa ke rangkaian ekivalen yang terdiri dari sumber tegangan tunggal dan resistansi seri. Resistansi beban kemudian dapat dihubungkan kembali ke "sirkuit ekivalen Thevenin" ini dan perhitungan dilakukan seolah-olah seluruh jaringan hanyalah rangkaian seri sederhana:

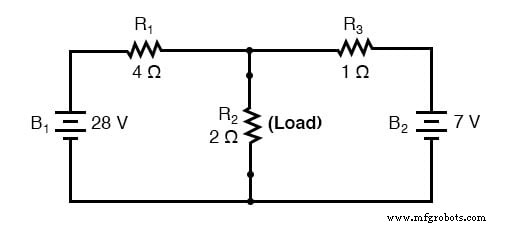
. . . setelah konversi Thevenin. . .

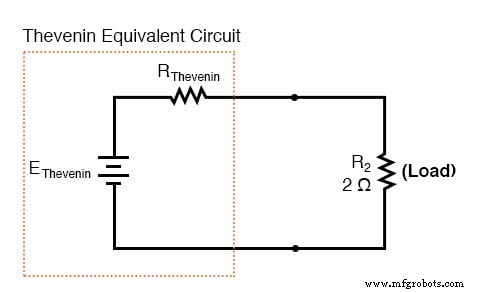
"Sirkuit Setara Thevenin" adalah ekivalen listrik dari B₁ , R₁ , R₃ , dan B₂ dilihat dari dua titik dimana resistor beban kita (R₂ ) terhubung.

Rangkaian ekivalen Thevenin, jika diturunkan dengan benar, akan berperilaku sama persis dengan rangkaian asli yang dibentuk oleh B₁ , R₁ , R₃ , dan B₂ . Dengan kata lain, resistor beban (R₂ ) tegangan dan arus harus sama persis untuk nilai hambatan beban yang sama pada kedua rangkaian. Resistor beban R₂ tidak dapat "membedakan" antara jaringan asli B₁ , R₁ , R₃ , dan B₂ , dan rangkaian ekivalen Thevenin dari E_Thevenin , dan R_Thevenin , asalkan nilai untuk E_Thevenin dan R_Thevenin telah dihitung dengan benar.

Keuntungan dalam melakukan "konversi Thevenin" ke rangkaian yang lebih sederhana, tentu saja, adalah membuat tegangan beban dan arus beban jauh lebih mudah untuk diselesaikan daripada di jaringan asli. Menghitung tegangan sumber Thevenin yang setara dan resistansi seri sebenarnya cukup mudah. Pertama, resistor beban yang dipilih dilepas dari rangkaian aslinya, diganti dengan pemutus (rangkaian terbuka):

Tentukan Tegangan Thevenin

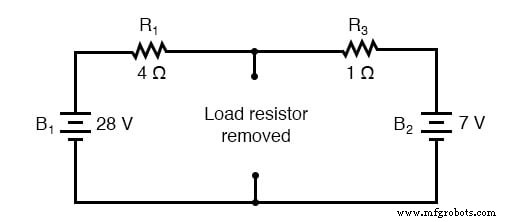
Selanjutnya, tegangan antara dua titik di mana resistor beban yang digunakan untuk dipasang ditentukan. Gunakan metode analisis apa pun yang Anda inginkan untuk melakukan ini. Dalam hal ini, rangkaian asli dengan resistor beban dilepas tidak lebih dari rangkaian seri sederhana dengan baterai yang berlawanan, sehingga kita dapat menentukan tegangan melintasi terminal beban terbuka dengan menerapkan aturan rangkaian seri, Hukum Ohm, dan Tegangan Kirchhoff Hukum:

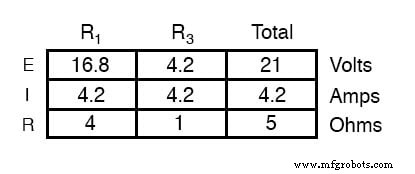
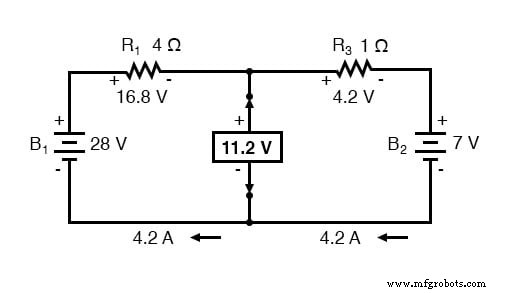
Tegangan antara dua titik sambungan beban dapat ditentukan dari salah satu tegangan baterai dan salah satu tegangan resistor turun dan keluar menjadi 11,2 volt. Ini adalah "tegangan Thevenin" kami (E_Thevenin ) dalam rangkaian ekivalen:

Tentukan Resistansi Deret Thevenin

Untuk menemukan resistansi seri Thevenin untuk rangkaian ekivalen kita, kita perlu mengambil rangkaian asli (dengan resistor beban masih dilepas), lepaskan sumber daya (dengan gaya yang sama seperti yang kita lakukan dengan Teorema Superposisi:sumber tegangan diganti dengan kabel dan sumber arus diganti dengan pemutusan), dan hitung hambatan dari satu terminal beban ke terminal beban lainnya:

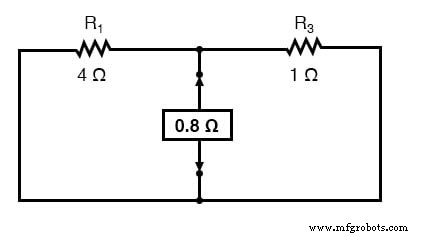
Dengan melepas kedua baterai, resistansi total yang diukur di lokasi ini sama dengan R₁ dan R₃ paralel:0,8 . Ini adalah "perlawanan Thevenin" kami (R_Thevenin ) untuk rangkaian ekivalen:

Tentukan Tegangan Pada Resistor Beban

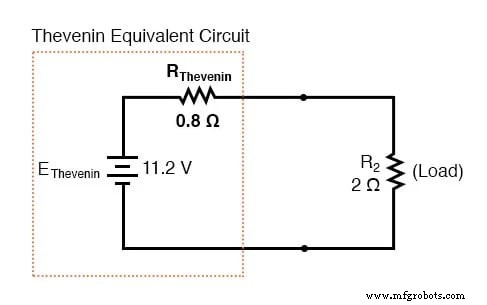
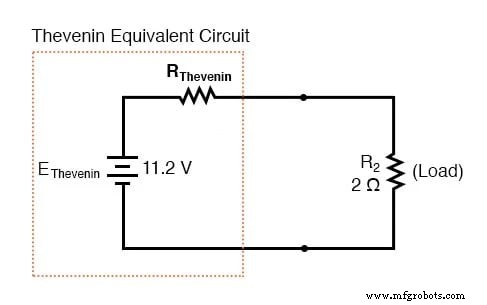
Dengan resistor beban (2 ) yang terpasang di antara titik-titik sambungan, kita dapat menentukan tegangan yang melintasinya dan arus yang melaluinya seolah-olah seluruh jaringan tidak lebih dari rangkaian seri sederhana:

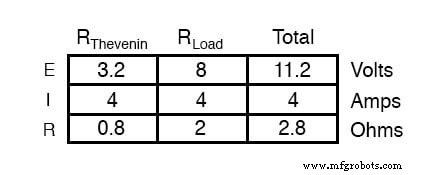
Perhatikan bahwa angka tegangan dan arus untuk R₂ (8 volt, 4 amp) identik dengan yang ditemukan menggunakan metode analisis lain. Perhatikan juga bahwa angka tegangan dan arus untuk resistansi seri Thevenin dan sumber Thevenin (total ) tidak berlaku untuk komponen apa pun di sirkuit asli yang kompleks. Teorema Thevenin hanya berguna untuk menentukan apa yang terjadi pada tunggal resistor dalam jaringan:beban.

Keuntungannya, tentu saja, adalah Anda dapat dengan cepat menentukan apa yang akan terjadi pada resistor tunggal itu jika nilainya selain 2 tanpa harus melalui banyak analisis lagi. Cukup colokkan nilai lain untuk resistor beban ke dalam rangkaian ekivalen Thevenin dan sedikit perhitungan rangkaian seri akan memberi Anda hasilnya.

TINJAUAN:

• Teorema Thevenin adalah cara untuk mereduksi jaringan menjadi rangkaian ekivalen yang terdiri dari sumber tegangan tunggal, resistansi seri, dan beban seri.
• Langkah yang harus diikuti untuk Teorema Thevenin:
  • Temukan tegangan sumber Thevenin dengan melepaskan resistor beban dari rangkaian asli dan menghitung tegangan di seluruh titik koneksi terbuka tempat resistor beban dulu berada.
  • Temukan resistansi Thevenin dengan melepas semua sumber daya di sirkuit asli (sumber tegangan korsleting dan sumber arus terbuka) dan menghitung resistansi total antara titik koneksi terbuka.
  • Gambar rangkaian ekivalen Thevenin, dengan sumber tegangan Thevenin dirangkai secara seri dengan hambatan Thevenin. Resistor beban dipasang kembali di antara dua titik terbuka dari rangkaian ekivalen.
  • Analisis tegangan dan arus untuk resistor beban dengan mengikuti aturan rangkaian seri.

LEMBAR KERJA TERKAIT:

• Lembar Kerja Teorema Transfer Daya Thevenin, Norton, dan Maksimum