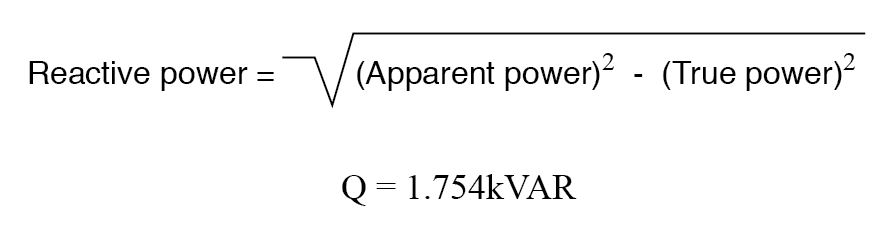Kekuatan Nyata, Reaktif, dan Nyata
Daya Reaktif
Kita tahu bahwa beban reaktif seperti induktor dan kapasitor menghilangkan daya nol, namun fakta bahwa mereka menjatuhkan tegangan dan menarik arus memberikan kesan menipu bahwa mereka benar-benar melakukannya menghilangkan daya.
"Kekuatan hantu" ini disebut kekuatan reaktif , dan diukur dalam satuan yang disebut Volt-Amps-Reactive (VAR), bukan watt.
Simbol matematika untuk daya reaktif adalah (sayangnya) huruf kapital Q.
Kekuatan Sejati
Jumlah daya yang sebenarnya digunakan, atau dihamburkan, dalam suatu rangkaian disebut daya sejati , dan diukur dalam watt (dilambangkan dengan huruf kapital P, seperti biasa).
Kekuatan Nyata
Kombinasi daya reaktif dan daya sebenarnya disebut daya semu , dan itu adalah produk dari tegangan dan arus sirkuit, tanpa mengacu pada sudut fase.
Daya semu diukur dalam satuan Volt-Amps (VA) dan dilambangkan dengan huruf kapital S.
Menghitung Daya Reaktif, Benar, atau Nyata
Sebagai aturan, daya sebenarnya adalah fungsi dari elemen disipatif rangkaian, biasanya resistansi (R). Daya reaktif adalah fungsi dari reaktansi rangkaian (X).
Daya semu adalah fungsi dari impedansi total rangkaian (Z). Karena kita berurusan dengan besaran skalar untuk perhitungan daya, setiap besaran awal yang kompleks seperti tegangan, arus, dan impedansi harus diwakili oleh besarnya kutub , bukan dengan komponen persegi panjang nyata atau imajiner.
Misalnya, jika saya menghitung daya sebenarnya dari arus dan hambatan, saya harus menggunakan besaran kutub untuk arus, dan bukan hanya bagian arus "nyata" atau "imajiner".
Jika saya menghitung daya semu dari tegangan dan impedansi, kedua besaran yang sebelumnya kompleks ini harus dikurangi menjadi besaran kutubnya untuk aritmatika skalar.
Persamaan Menggunakan Besaran Skalar
Ada beberapa persamaan daya yang menghubungkan ketiga jenis daya dengan resistansi, reaktansi, dan impedansi (semua menggunakan besaran skalar):

Harap diperhatikan bahwa masing-masing ada dua persamaan untuk penghitungan daya sebenarnya dan daya reaktif.
Ada tiga persamaan yang tersedia untuk penghitungan daya semu, P=IE berguna hanya untuk tujuan itu.
Periksa rangkaian berikut dan lihat bagaimana ketiga jenis daya ini saling berhubungan untuk:beban resistif murni, beban reaktif murni, dan beban resistif/reaktif.
Hanya Beban Resistif
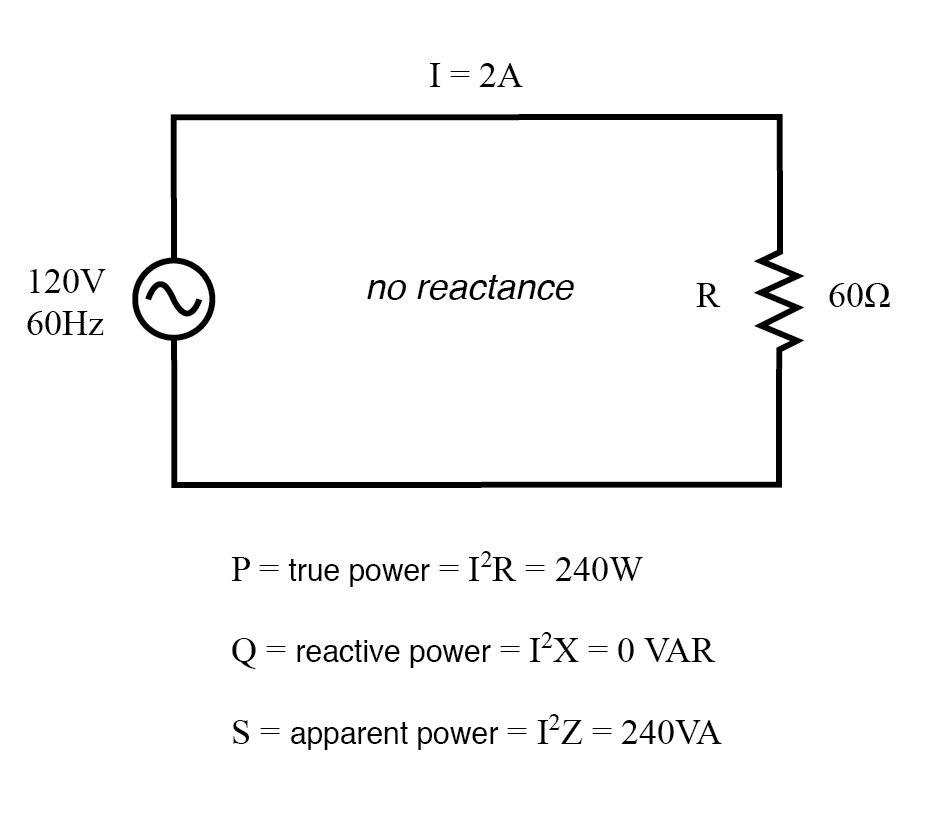
Daya sebenarnya, daya reaktif, dan daya semu untuk beban resistif murni.
Hanya Muatan Reaktif
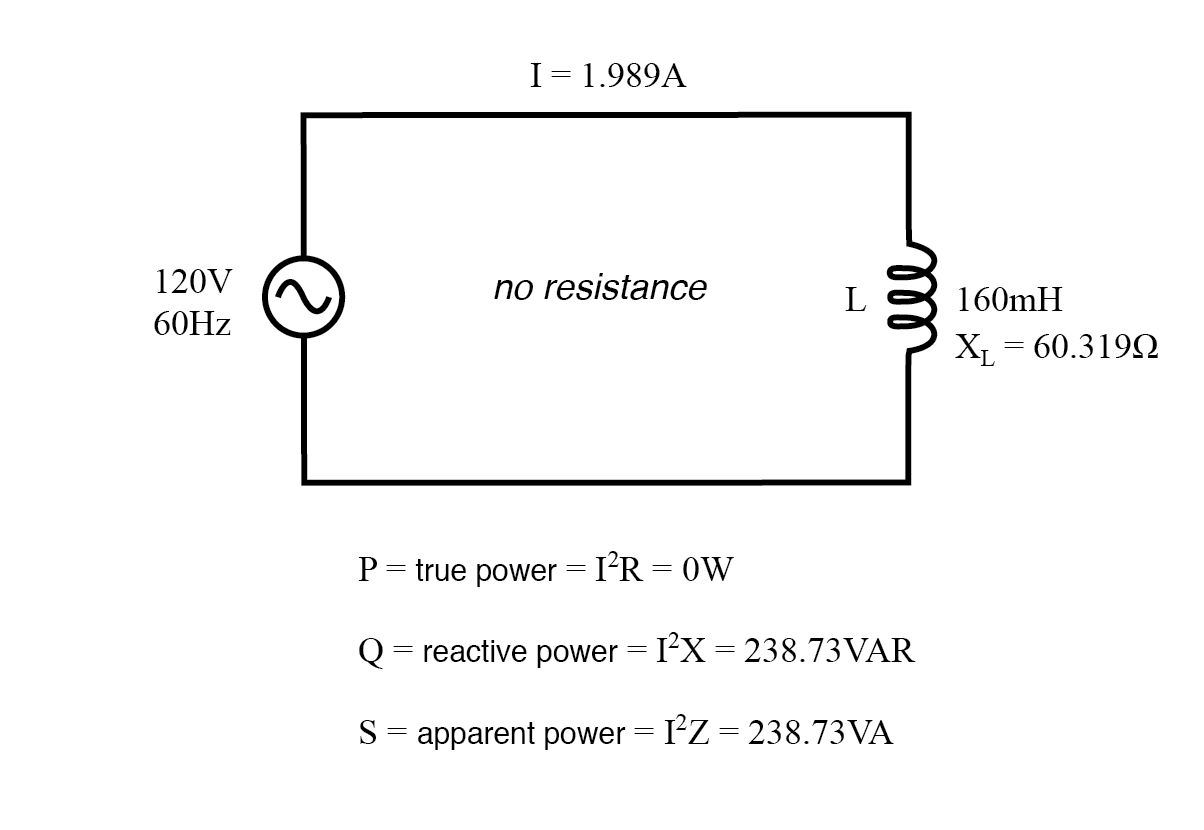
Daya sebenarnya, daya reaktif, dan daya nyata untuk beban reaktif murni.
Beban Resistif/Reaktif
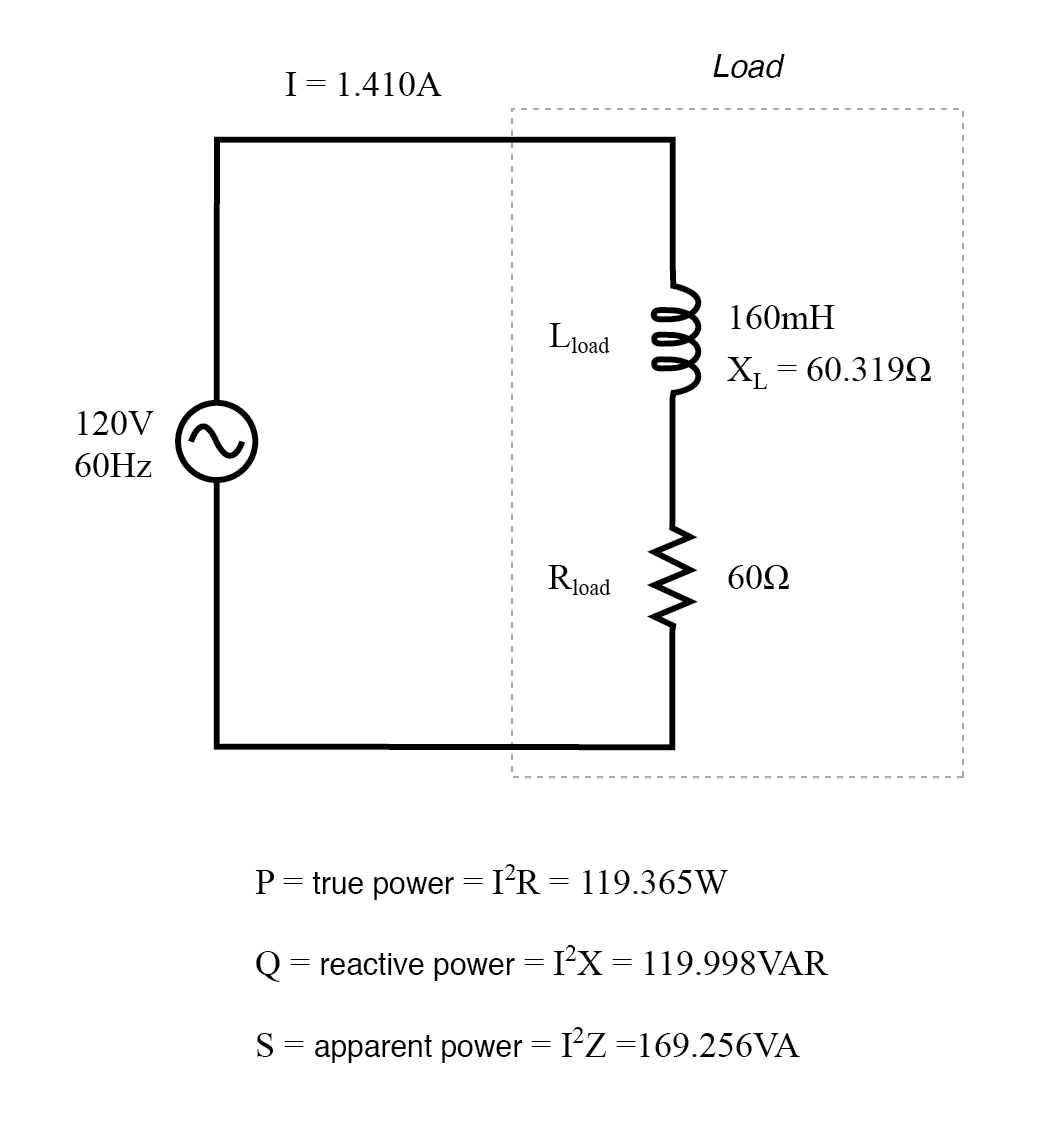
Daya sebenarnya, daya reaktif, dan daya semu untuk beban resistif/reaktif.
Segitiga Kekuatan
Ketiga jenis daya ini—benar, reaktif, dan nyata—berhubungan satu sama lain dalam bentuk trigonometri. Kami menyebutnya segitiga kekuatan :(Gambar di bawah).
Segitiga daya menghubungkan daya semu dengan daya sebenarnya dan daya reaktif.
Dengan menggunakan hukum trigonometri, kita dapat menyelesaikan panjang salah satu sisi (jumlah jenis daya apa pun), mengingat panjang kedua sisi lainnya, atau panjang satu sisi dan sebuah sudut.
TINJAUAN:
- Daya yang dihamburkan oleh beban disebut sebagai daya sejati . Kekuatan sebenarnya dilambangkan dengan huruf P dan diukur dalam satuan Watt (W).
- Daya yang hanya diserap dan dikembalikan dalam beban karena sifat reaktifnya disebut sebagai daya reaktif . Daya reaktif dilambangkan dengan huruf Q dan diukur dalam satuan Volt-Amps-Reactive (VAR).
- Total daya dalam rangkaian AC, baik yang hilang maupun yang diserap/dikembalikan disebut sebagai daya semu . Daya semu dilambangkan dengan huruf S dan diukur dalam satuan Volt-Amp (VA).
- Ketiga jenis kekuatan ini secara trigonometri terkait satu sama lain. Pada segitiga siku-siku, P =panjang sisi, Q =panjang berhadapan, dan S =panjang sisi miring. Sudut yang berlawanan sama dengan sudut fase impedansi (Z) rangkaian.
LEMBAR KERJA TERKAIT: