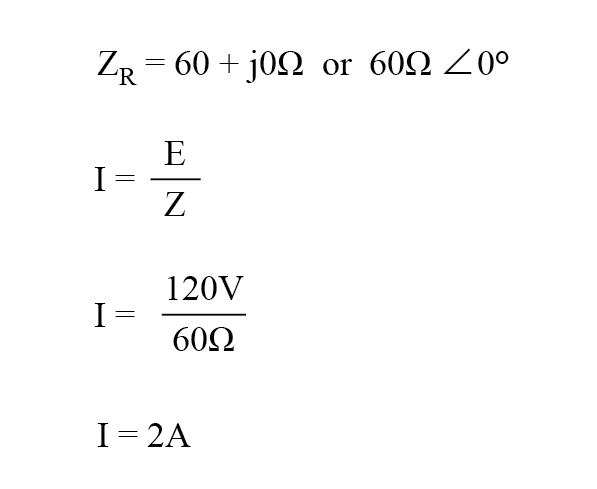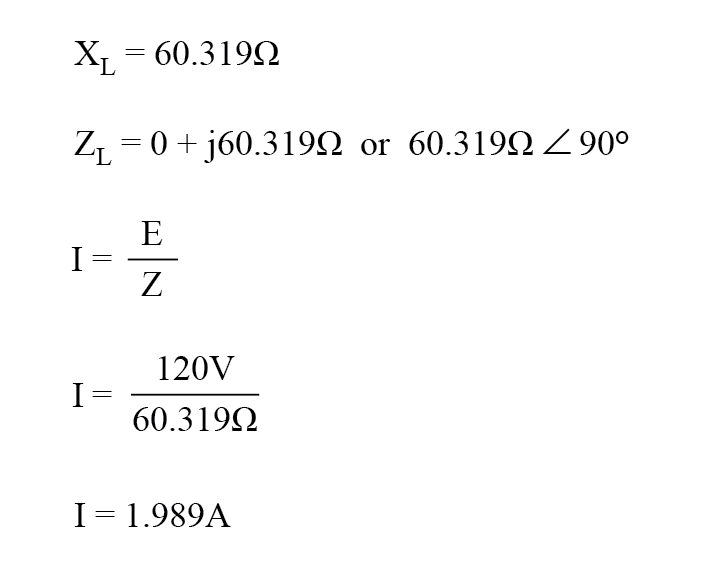Daya dalam rangkaian AC Resistif dan Reaktif

Pertimbangkan rangkaian untuk sistem daya AC satu fase, di mana sumber tegangan AC 120 volt, 60 Hz mengirimkan daya ke beban resistif:(Gambar di bawah)

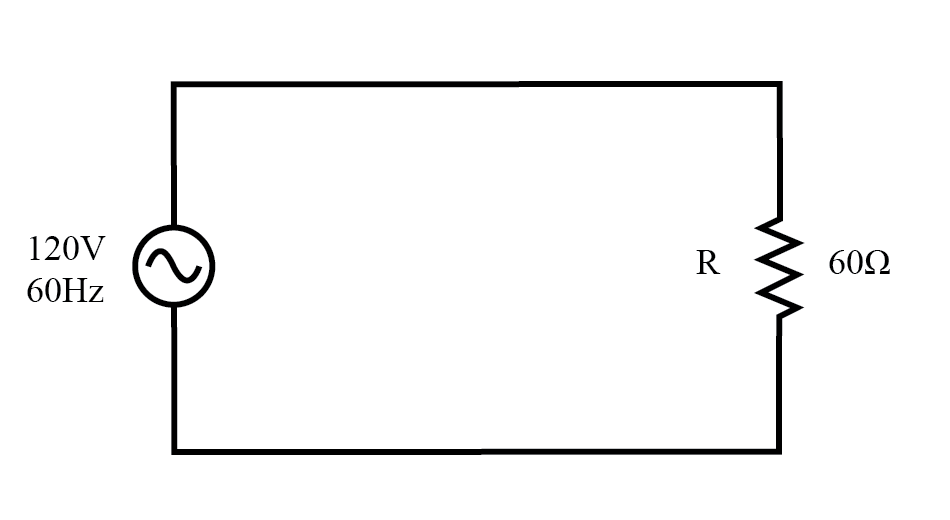
Sumber AC menggerakkan beban resistif murni.

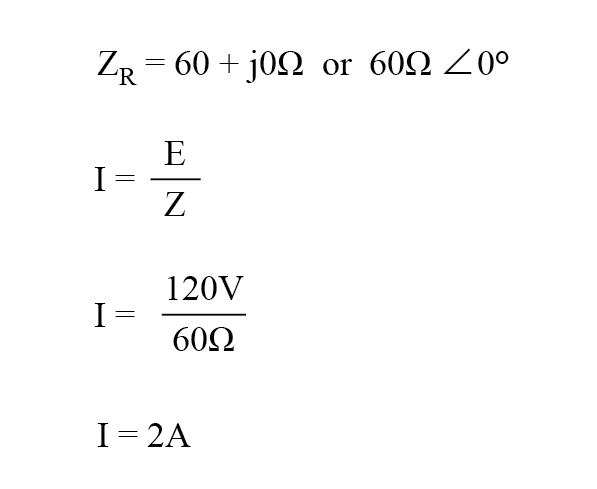
Dalam contoh ini, arus ke beban adalah 2 amp, RMS. Daya yang hilang pada beban akan menjadi 240 watt.

Karena beban ini murni resistif (tidak ada reaktansi), arus sefasa dengan tegangan, dan perhitungannya mirip dengan rangkaian DC ekivalen.

Jika kita memplot bentuk gelombang tegangan, arus, dan daya untuk rangkaian ini, maka akan terlihat seperti gambar di bawah ini.

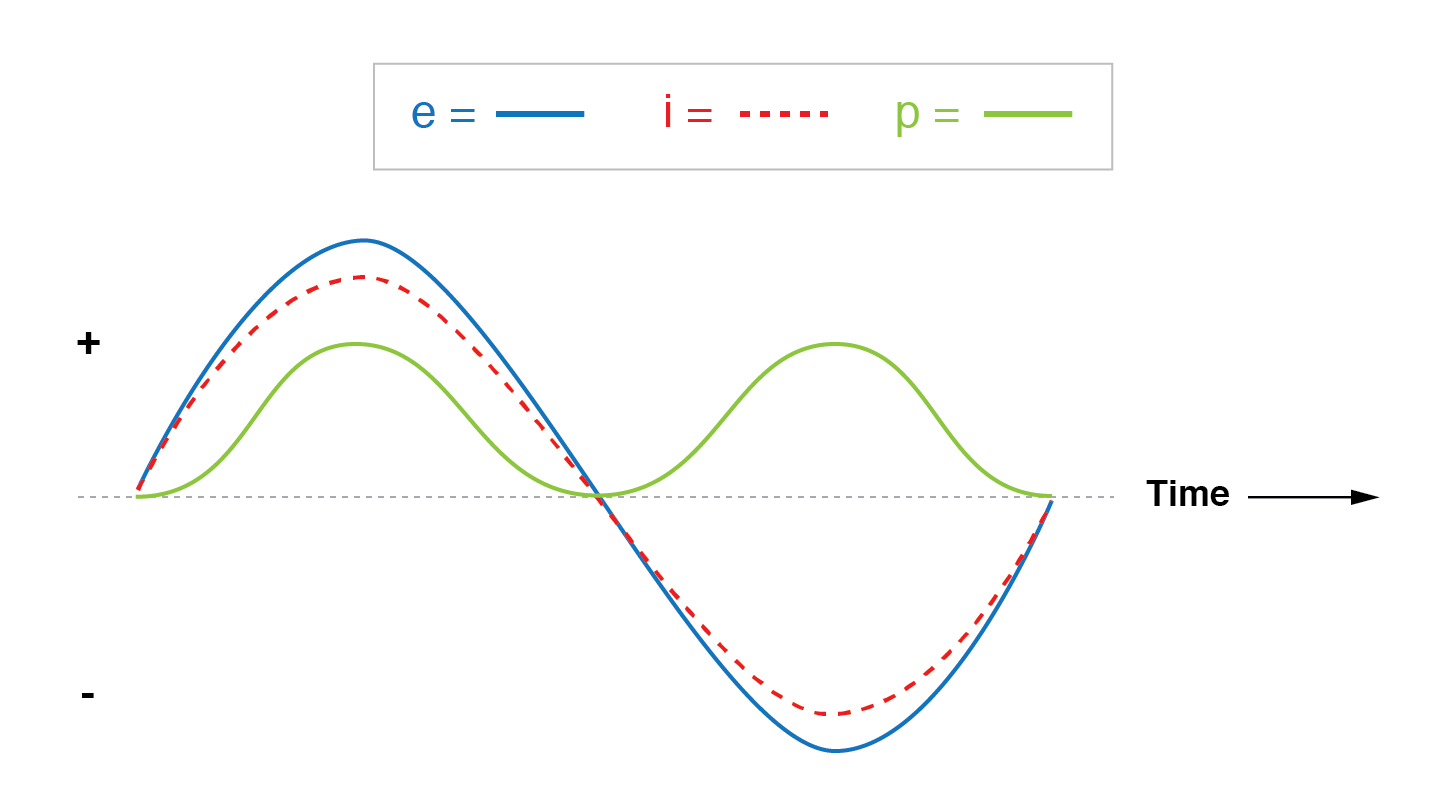
Arus sefasa dengan tegangan dalam rangkaian resistif.

Perhatikan bahwa bentuk gelombang untuk daya selalu positif, tidak pernah negatif untuk rangkaian resistif ini.

Ini berarti bahwa daya selalu dihamburkan oleh beban resistif, dan tidak pernah kembali ke sumbernya seperti pada beban reaktif. Jika sumbernya adalah generator mekanis, dibutuhkan energi mekanik sebesar 240 watt (sekitar 1/3 tenaga kuda) untuk memutar poros.

Juga, perhatikan bahwa bentuk gelombang untuk daya tidak pada frekuensi yang sama dengan tegangan atau arus! Sebaliknya, frekuensinya ganda bentuk gelombang tegangan atau arus.

Frekuensi yang berbeda ini melarang ekspresi daya dalam rangkaian AC menggunakan notasi kompleks (persegi panjang atau kutub) yang sama seperti yang digunakan untuk tegangan, arus, dan impedansi karena bentuk simbolisme matematika ini menyiratkan hubungan fase yang tidak berubah.

Ketika frekuensi tidak sama, hubungan fase terus berubah.

Meski terlihat aneh, cara terbaik untuk melanjutkan penghitungan daya AC adalah dengan menggunakan skalar notasi dan untuk menangani hubungan fase yang relevan dengan trigonometri.

Sirkuit AC dengan beban Reaktif Murni

Sebagai perbandingan, mari kita lihat rangkaian AC sederhana dengan beban reaktif murni pada gambar di bawah.

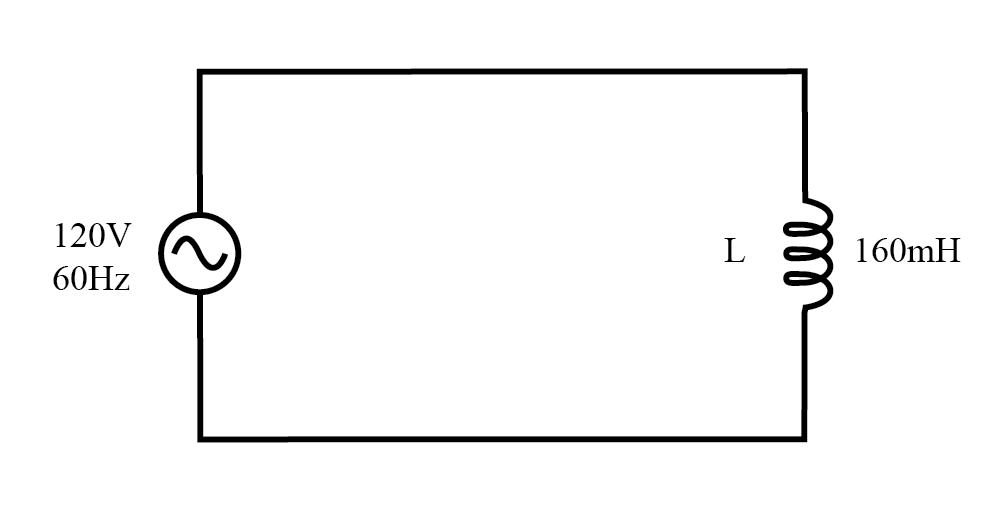
Sirkuit AC dengan beban reaktif murni (induktif).

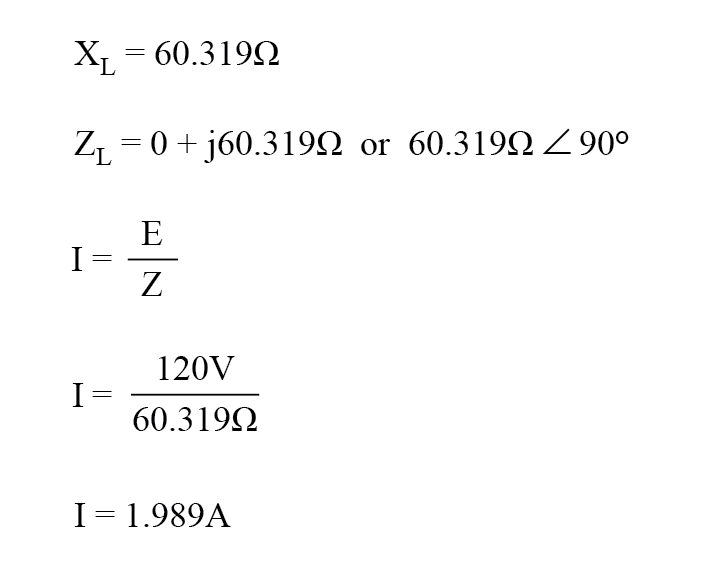
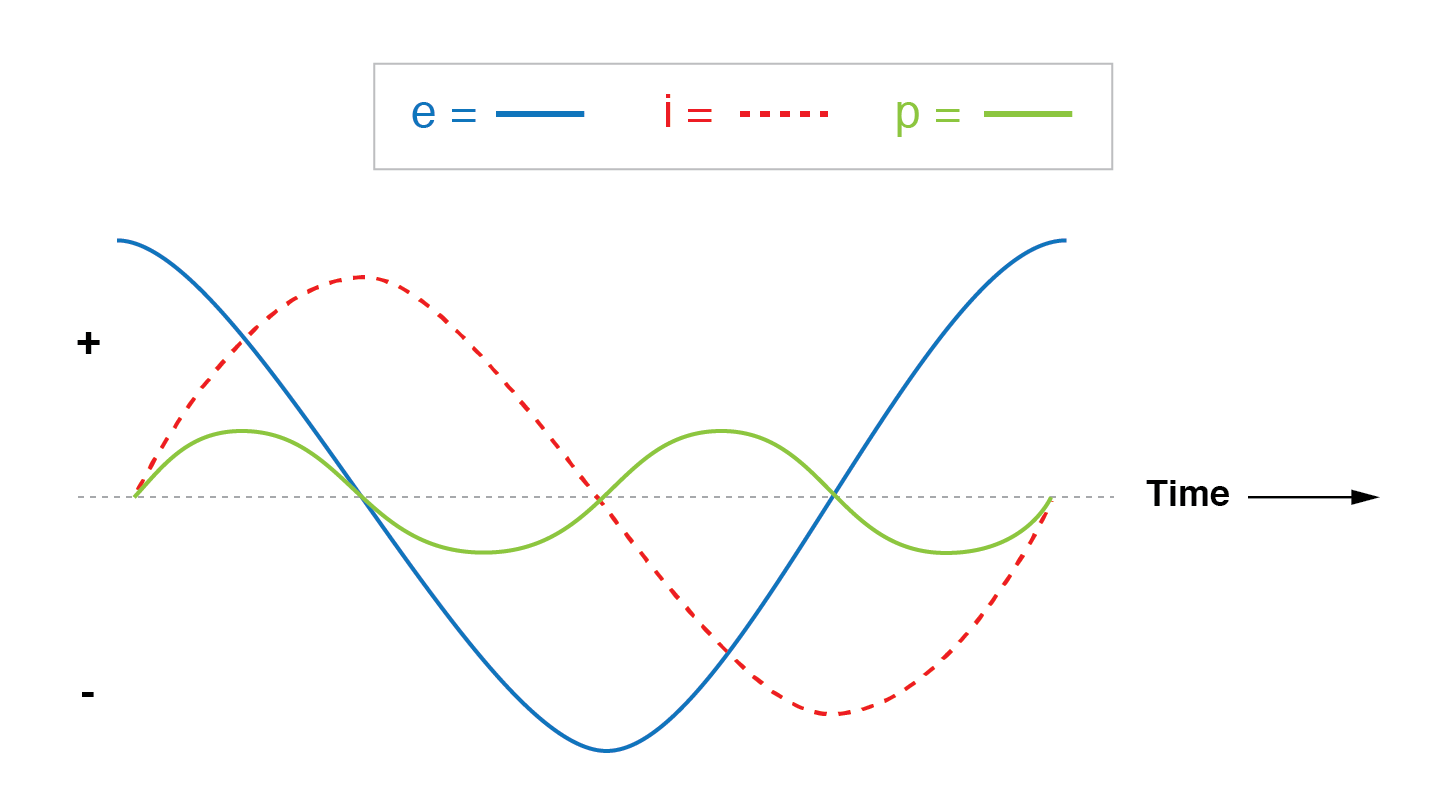
Daya tidak hilang dalam beban reaktif murni. Meskipun secara bergantian diserap dari dan dikembalikan ke sumbernya.

Perhatikan bahwa daya bergantian sama antara siklus positif dan negatif. (Gambar di atas) Ini berarti bahwa daya secara bergantian diserap dari dan dikembalikan ke sumbernya.

Jika sumbernya adalah generator mekanis, (praktis) tidak diperlukan energi mekanik bersih untuk memutar poros, karena tidak ada daya yang digunakan oleh beban.

Poros generator akan mudah berputar, dan induktor tidak akan menjadi hangat seperti resistor.

Sirkuit AC dengan beban Resistif dan Reaktif Murni

Sekarang, mari kita perhatikan rangkaian AC dengan beban yang terdiri dari induktansi dan resistansi pada gambar di bawah ini.

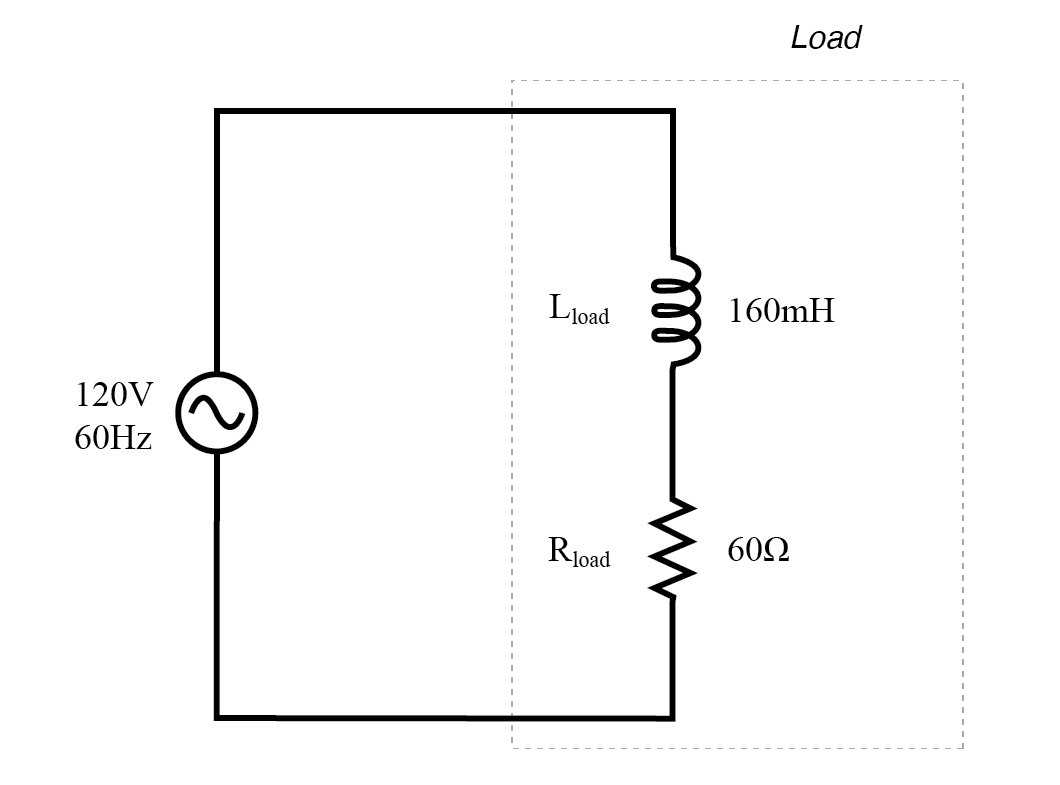
Sirkuit AC dengan reaktansi dan resistansi.

Pada frekuensi 60 Hz, induktansi 160 milihenry menghasilkan 60,319 reaktansi induktif.

Reaktansi ini bergabung dengan resistansi 60 untuk membentuk impedansi beban total 60 + j60.319 , atau 85.078 45.152 ^o . Jika kita tidak memperhatikan sudut fase (yang tidak kita bahas pada saat ini), kita dapat menghitung arus dalam rangkaian dengan mengambil besaran kutub dari sumber tegangan (120 volt) dan membaginya dengan besaran kutub dari impedansi (85.078 ).

Dengan tegangan catu daya 120 volt RMS, arus beban kami adalah 1,410 amp. Ini adalah angka yang akan ditunjukkan oleh ammeter RMS jika dihubungkan secara seri dengan resistor dan induktor.

Kita sudah tahu bahwa komponen reaktif menghilangkan daya nol, karena mereka sama-sama menyerap daya dari, dan mengembalikan daya ke, sisa rangkaian.

Oleh karena itu, setiap reaktansi induktif dalam beban ini juga akan menghilangkan daya nol.

Satu-satunya yang tersisa untuk menghilangkan daya di sini adalah bagian resistif dari impedansi beban. Jika kita melihat plot bentuk gelombang tegangan, arus, dan daya total untuk rangkaian ini, kita melihat bagaimana kombinasi ini bekerja pada gambar di bawah.

Sebuah rangkaian resistif/reaktif gabungan menghamburkan lebih banyak daya daripada yang dikembalikan ke sumbernya. Reaktansi tidak menghilangkan daya; meskipun, resistornya.

Seperti halnya sirkuit reaktif, daya bergantian antara nilai instan positif dan negatif dari waktu ke waktu.

Dalam rangkaian reaktif murni, pergantian antara daya positif dan negatif dibagi rata, menghasilkan disipasi daya bersih nol. Namun, dalam rangkaian dengan resistansi dan reaktansi campuran seperti ini, bentuk gelombang daya akan tetap bergantian antara positif dan negatif, tetapi jumlah daya positif akan melebihi jumlah daya negatif.

Dengan kata lain, beban induktif/resistif gabungan akan mengkonsumsi lebih banyak daya daripada yang dikembalikan ke sumbernya.

Melihat plot bentuk gelombang untuk daya, harus terbukti bahwa gelombang menghabiskan lebih banyak waktu di sisi positif dari garis tengah daripada di sisi negatif, menunjukkan bahwa ada lebih banyak daya yang diserap oleh beban daripada yang dikembalikan ke rangkaian.

Sedikit kembalinya daya yang terjadi karena reaktansi; ketidakseimbangan daya positif versus daya negatif disebabkan oleh hambatan karena ia menghilangkan energi di luar rangkaian (biasanya dalam bentuk panas).

Jika sumbernya adalah generator mekanis, jumlah energi mekanik yang dibutuhkan untuk memutar poros akan menjadi jumlah daya rata-rata antara siklus daya positif dan negatif.

Mewakili daya secara matematis dalam rangkaian AC merupakan suatu tantangan, karena gelombang daya tidak berada pada frekuensi yang sama dengan tegangan atau arus.

Selanjutnya, sudut fasa untuk daya berarti sesuatu yang sangat berbeda dari sudut fasa untuk tegangan atau arus. Sedangkan sudut tegangan atau arus mewakili pergeseran waktu relatif antara dua gelombang, sudut fase untuk daya mewakili rasio antara daya yang hilang dan daya yang dikembalikan.

Karena perbedaan daya AC dari tegangan atau arus AC ini, sebenarnya lebih mudah untuk mendapatkan angka daya dengan menghitung dengan skalar jumlah tegangan, arus, hambatan, dan reaktansi daripada mencoba menurunkannya dari vektor , atau kompleks jumlah tegangan, arus, dan impedansi yang telah kami kerjakan sejauh ini.

TINJAUAN:

• Dalam rangkaian resistif murni, semua daya rangkaian dihamburkan oleh resistor. Tegangan dan arus berada dalam fase satu sama lain.
• Dalam rangkaian reaktif murni, tidak ada daya rangkaian yang dihamburkan oleh beban. Sebaliknya, daya secara bergantian diserap dari dan dikembalikan ke sumber AC. Tegangan dan arus berbeda fase 90° satu sama lain.
• Dalam rangkaian yang terdiri dari campuran resistansi dan reaktansi, akan ada lebih banyak daya yang dihamburkan oleh beban daripada yang dikembalikan, tetapi sebagian daya pasti akan dihamburkan dan sebagian hanya akan diserap dan dikembalikan. Tegangan dan arus dalam rangkaian seperti itu akan keluar fase dengan nilai antara 0° dan 90°.

LEMBAR KERJA TERKAIT:

• Lembar Kerja Daya AC