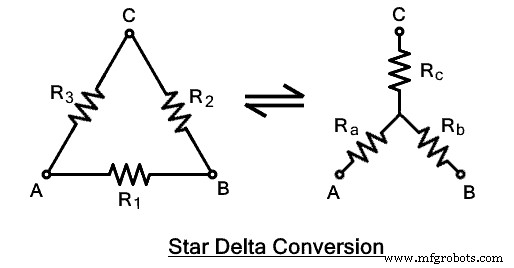
Konversi Bintang ke Delta &Delta ke Bintang. Transformasi Y-Δ
Transformasi Bintang ke Delta dan Delta ke Bintang – Konversi Y-Δ
Dalam jaringan listrik, impedansi dapat dihubungkan dalam berbagai konfigurasi. Yang paling umum dari konfigurasi ini adalah jaringan yang terhubung bintang atau delta. Untuk menyelesaikan jaringan listrik yang kompleks atau menyederhanakannya, kami menggunakan teknik konversi bintang-delta. Ini menggantikan jaringan yang terhubung bintang dengan jaringan terhubung delta yang setara &sebaliknya. Kami akan memberikan turunan rumus singkat untuk konversi beban antara beban terhubung bintang dan delta.

Konversi Delta Bintang
Kita tahu dasar dari seri, paralel atau kombinasi seri dan koneksi paralel tetapi Y-Δ adalah konfigurasi komponen yang sedikit rumit. Jaringan 3 fase memiliki tiga kabel dan biasanya, jaringan terhubung dalam konfigurasi bintang &delta . Suplai 3 fasa atau beban yang terhubung dalam salah satu formasi dapat diubah menjadi pasangan ekuivalennya. Kami menggunakan konversi tersebut untuk menyederhanakan perhitungan matematis yang diperlukan untuk analisis rangkaian jaringan listrik yang kompleks.
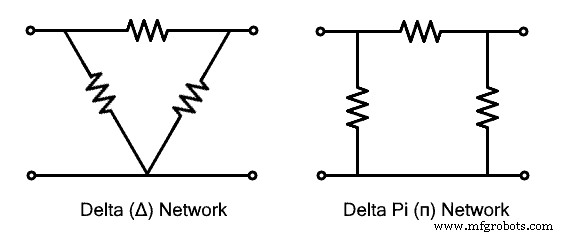
Jaringan Terhubung Delta
Jaringan terhubung delta terbentuk ketika tiga cabang jaringan atau impedansi dihubungkan untuk membentuk loop sedemikian rupa sehingga kepala mereka terhubung ke ekor cabang yang berdekatan. Jaringan yang dihasilkan membentuk bentuk segitiga yang menyerupai huruf Yunani Delta "Δ" itulah sebabnya dinamai menurut namanya. Ini juga dikenal sebagai jaringan (pi) karena menyerupai huruf setelah mengatur ulang cabang. Ketahui lebih banyak tentang Koneksi Delta di postingan sebelumnya.
Jaringan Terhubung Bintang
Jaringan terhubung Bintang terbentuk ketika tiga cabang atau impedansi dihubungkan bersama pada titik yang sama. Ujung lain dari jaringan cabang bebas. Bentuk yang dihasilkan menyerupai huruf “Y” itulah sebabnya disebut juga jaringan terhubung “Y” atau “Wye”. Ini juga dikenal sebagai jaringan terhubung "T" karena bentuknya setelah mengatur ulang cabang-cabang jaringan. Ketahui lebih banyak tentang Star Connection di postingan sebelumnya. 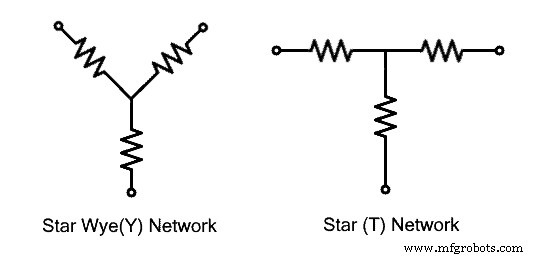 Rangkaian yang diberikan di atas dapat dikonversi menggunakan transformasi berikut. Selama transformasi, terminal A, B, C harus tetap pada posisi yang sama, hanya impedansi &susunannya yang berubah. Gambar berikut mengilustrasikan pernyataan yang diberikan di atas.
Rangkaian yang diberikan di atas dapat dikonversi menggunakan transformasi berikut. Selama transformasi, terminal A, B, C harus tetap pada posisi yang sama, hanya impedansi &susunannya yang berubah. Gambar berikut mengilustrasikan pernyataan yang diberikan di atas.
Konversi Delta ke Bintang
Jaringan terhubung delta dapat diubah menjadi konfigurasi bintang menggunakan serangkaian rumus listrik. Mari kita turunkan persamaan untuk setiap impedansi. 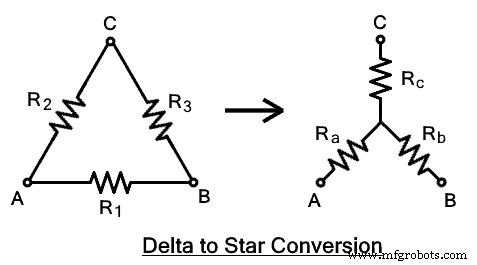 Gambar berikut menunjukkan jaringan delta yang memiliki terminal A, B, C dengan impedansi R1 , R2 , R3 . Jaringan terhubung bintang yang setara dengan RA , RB &RC di mana mereka terhubung ke terminal yang sesuai seperti yang ditunjukkan pada gambar.
Gambar berikut menunjukkan jaringan delta yang memiliki terminal A, B, C dengan impedansi R1 , R2 , R3 . Jaringan terhubung bintang yang setara dengan RA , RB &RC di mana mereka terhubung ke terminal yang sesuai seperti yang ditunjukkan pada gambar.
Seperti disebutkan sebelumnya, terminal A, B, C tetap sama, serta impedansi di antara keduanya, harus tetap sama.
Total impedansi antara A-B dalam jaringan delta; 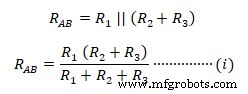 Demikian pula impedansi antar terminal B-C
Demikian pula impedansi antar terminal B-C 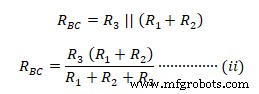 Demikian pula impedansi antara A-C
Demikian pula impedansi antara A-C 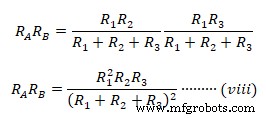 Menurut jaringan bintang;
Menurut jaringan bintang;
RAB =RA + RB
RBC =RB + RC
RAC =RA + RC
Sekarang tambahkan persamaan (i), (ii) &(iii) bersama-sama 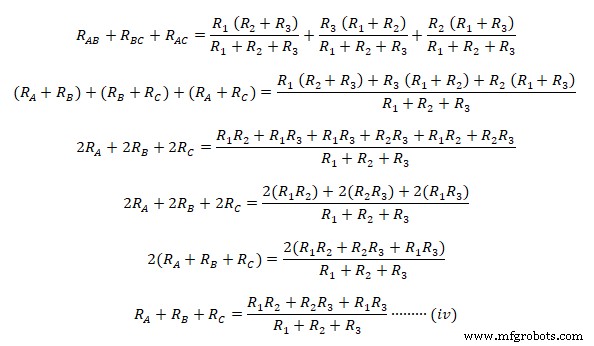 Sekarang kurangi persamaan (i), (ii), &(iii) satu per satu dari persamaan (iv)
Sekarang kurangi persamaan (i), (ii), &(iii) satu per satu dari persamaan (iv)
Pertama, Kurangi (ii) dari (iv) 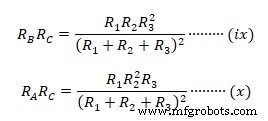 Pengurangan yang sama (i) &(iii) dari (iv) menghasilkan
Pengurangan yang sama (i) &(iii) dari (iv) menghasilkan 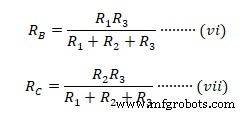 Dari persamaan turunan untuk impedansi setara bintang RA , RB , &RC kita dapat menyimpulkan hubungan antara konversi delta-ke-bintang sebagai; impedansi bintang ekivalen sama dengan produk dari impedansi delta yang berdekatan dengan terminal dibagi dengan jumlah dari ketiga impedansi delta.
Dari persamaan turunan untuk impedansi setara bintang RA , RB , &RC kita dapat menyimpulkan hubungan antara konversi delta-ke-bintang sebagai; impedansi bintang ekivalen sama dengan produk dari impedansi delta yang berdekatan dengan terminal dibagi dengan jumlah dari ketiga impedansi delta.
Jika ketiga Impedansi sama dalam jaringan delta, impedansi bintang setara akan menjadi
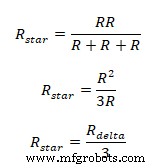 Karena semua impedansi di seluruh jaringan delta adalah sama, masing-masing tiga resistansi bintang setara akan menjadi 1/3 kali impedansi delta.
Karena semua impedansi di seluruh jaringan delta adalah sama, masing-masing tiga resistansi bintang setara akan menjadi 1/3 kali impedansi delta.
Konversi Bintang ke Delta
Sekarang kita akan mengubah impedansi terhubung bintang menjadi impedansi terhubung delta. Mari kita turunkan persamaan yang digunakan untuk konversi bintang ke delta.
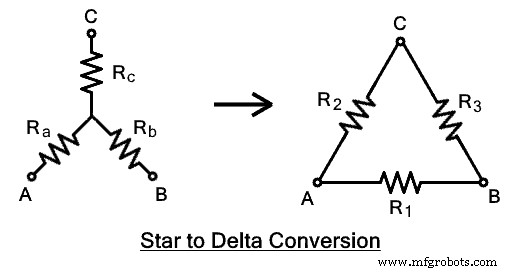 Gambar yang diberikan menunjukkan impedansi terhubung bintang RA , RB &RC. Sedangkan impedansi ekivalen delta yang dibutuhkan adalah R1 , R2 &R3 seperti yang ditunjukkan pada gambar.
Gambar yang diberikan menunjukkan impedansi terhubung bintang RA , RB &RC. Sedangkan impedansi ekivalen delta yang dibutuhkan adalah R1 , R2 &R3 seperti yang ditunjukkan pada gambar.
Untuk mencari resistansi delta ekivalen, kalikan persamaan sebelumnya (v) &(vi), serta (vi) &(vii) &(v) &( vii) bersama.
Perkalian (v) &(vi) 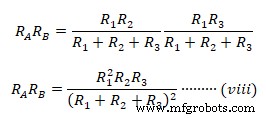 Serupa dengan mengalikan (vi) dengan (vii) &(v) dengan (vii)
Serupa dengan mengalikan (vi) dengan (vii) &(v) dengan (vii) 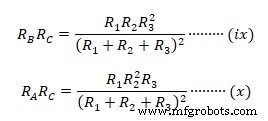
Sekarang tambahkan persamaan (viii), (ix) &(x) bersama-sama 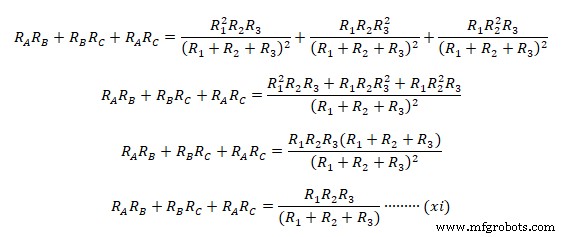 Untuk mendapatkan impedansi delta ekivalen individu, kita bagi persamaan (xi) dengan (v), (vi ) &(vii) secara terpisah seperti.
Untuk mendapatkan impedansi delta ekivalen individu, kita bagi persamaan (xi) dengan (v), (vi ) &(vii) secara terpisah seperti.
Membagi (xi) dengan (v) 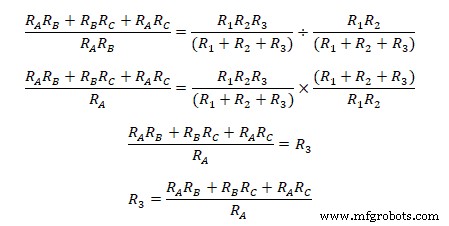 Membagi persamaan (xi) dengan (vi) &(vii) secara terpisah menghasilkan
Membagi persamaan (xi) dengan (vi) &(vii) secara terpisah menghasilkan
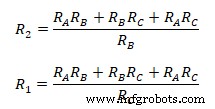 Hubungan antara impedansi ekivalen bintang ke delta jelas dari persamaan yang diberikan. Jumlah dari dua produk dari semua impedansi bintang dibagi dengan impedansi bintang dari terminal yang sesuai sama dengan impedansi delta yang terhubung dengan terminal yang berlawanan.
Hubungan antara impedansi ekivalen bintang ke delta jelas dari persamaan yang diberikan. Jumlah dari dua produk dari semua impedansi bintang dibagi dengan impedansi bintang dari terminal yang sesuai sama dengan impedansi delta yang terhubung dengan terminal yang berlawanan.
Menyederhanakan persamaan akan menghasilkan 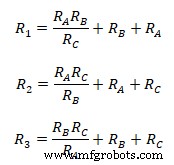 Jika semua impedansi bintang sama, impedansi delta ekivalennya adalah;
Jika semua impedansi bintang sama, impedansi delta ekivalennya adalah;
Menggunakan persamaan sebelumnya,
 Persamaan ini menunjukkan bahwa setiap impedansi delta ekivalen sama dengan 3 kali impedansi bintang.
Persamaan ini menunjukkan bahwa setiap impedansi delta ekivalen sama dengan 3 kali impedansi bintang.
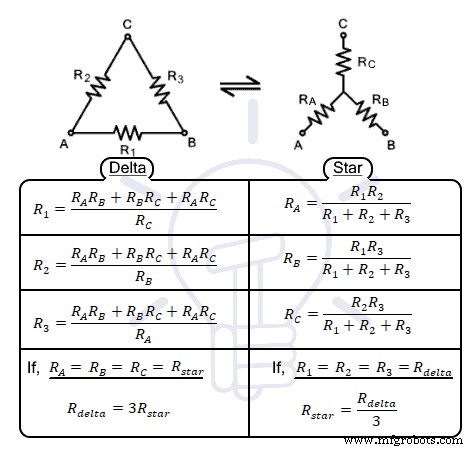







 Rangkaian yang diberikan di atas dapat dikonversi menggunakan transformasi berikut. Selama transformasi, terminal A, B, C harus tetap pada posisi yang sama, hanya impedansi &susunannya yang berubah. Gambar berikut mengilustrasikan pernyataan yang diberikan di atas.
Rangkaian yang diberikan di atas dapat dikonversi menggunakan transformasi berikut. Selama transformasi, terminal A, B, C harus tetap pada posisi yang sama, hanya impedansi &susunannya yang berubah. Gambar berikut mengilustrasikan pernyataan yang diberikan di atas. Gambar berikut menunjukkan jaringan delta yang memiliki terminal A, B, C dengan impedansi R1 , R2 , R3 . Jaringan terhubung bintang yang setara dengan RA , RB &RC di mana mereka terhubung ke terminal yang sesuai seperti yang ditunjukkan pada gambar.
Gambar berikut menunjukkan jaringan delta yang memiliki terminal A, B, C dengan impedansi R1 , R2 , R3 . Jaringan terhubung bintang yang setara dengan RA , RB &RC di mana mereka terhubung ke terminal yang sesuai seperti yang ditunjukkan pada gambar.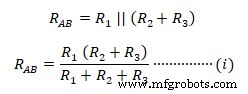 Demikian pula impedansi antar terminal B-C
Demikian pula impedansi antar terminal B-C 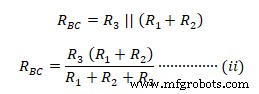 Demikian pula impedansi antara A-C
Demikian pula impedansi antara A-C 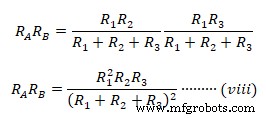 Menurut jaringan bintang;
Menurut jaringan bintang;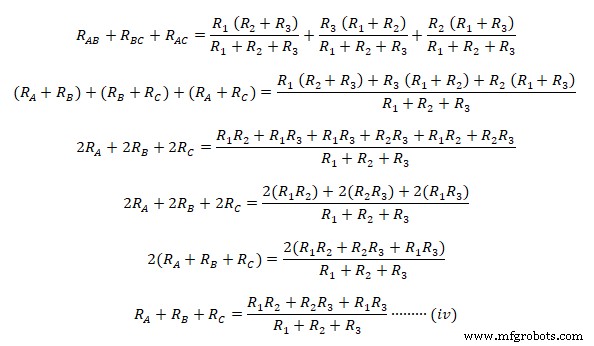 Sekarang kurangi persamaan (i), (ii), &(iii) satu per satu dari persamaan (iv)
Sekarang kurangi persamaan (i), (ii), &(iii) satu per satu dari persamaan (iv) 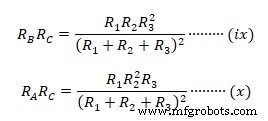 Pengurangan yang sama (i) &(iii) dari (iv) menghasilkan
Pengurangan yang sama (i) &(iii) dari (iv) menghasilkan 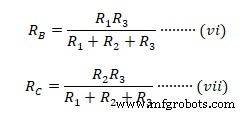 Dari persamaan turunan untuk impedansi setara bintang RA , RB , &RC kita dapat menyimpulkan hubungan antara konversi delta-ke-bintang sebagai; impedansi bintang ekivalen sama dengan produk dari impedansi delta yang berdekatan dengan terminal dibagi dengan jumlah dari ketiga impedansi delta.
Dari persamaan turunan untuk impedansi setara bintang RA , RB , &RC kita dapat menyimpulkan hubungan antara konversi delta-ke-bintang sebagai; impedansi bintang ekivalen sama dengan produk dari impedansi delta yang berdekatan dengan terminal dibagi dengan jumlah dari ketiga impedansi delta.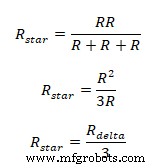 Karena semua impedansi di seluruh jaringan delta adalah sama, masing-masing tiga resistansi bintang setara akan menjadi 1/3 kali impedansi delta.
Karena semua impedansi di seluruh jaringan delta adalah sama, masing-masing tiga resistansi bintang setara akan menjadi 1/3 kali impedansi delta. Gambar yang diberikan menunjukkan impedansi terhubung bintang RA , RB &RC. Sedangkan impedansi ekivalen delta yang dibutuhkan adalah R1 , R2 &R3 seperti yang ditunjukkan pada gambar.
Gambar yang diberikan menunjukkan impedansi terhubung bintang RA , RB &RC. Sedangkan impedansi ekivalen delta yang dibutuhkan adalah R1 , R2 &R3 seperti yang ditunjukkan pada gambar.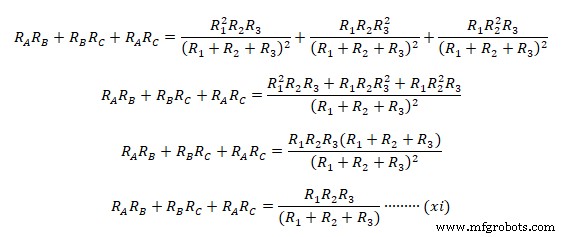 Untuk mendapatkan impedansi delta ekivalen individu, kita bagi persamaan (xi) dengan (v), (vi ) &(vii) secara terpisah seperti.
Untuk mendapatkan impedansi delta ekivalen individu, kita bagi persamaan (xi) dengan (v), (vi ) &(vii) secara terpisah seperti.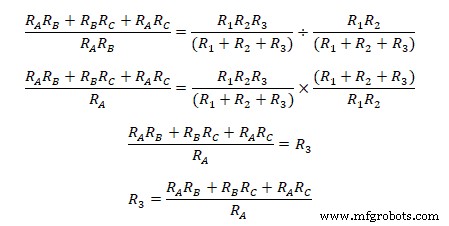 Membagi persamaan (xi) dengan (vi) &(vii) secara terpisah menghasilkan
Membagi persamaan (xi) dengan (vi) &(vii) secara terpisah menghasilkan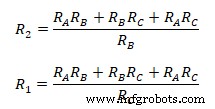 Hubungan antara impedansi ekivalen bintang ke delta jelas dari persamaan yang diberikan. Jumlah dari dua produk dari semua impedansi bintang dibagi dengan impedansi bintang dari terminal yang sesuai sama dengan impedansi delta yang terhubung dengan terminal yang berlawanan.
Hubungan antara impedansi ekivalen bintang ke delta jelas dari persamaan yang diberikan. Jumlah dari dua produk dari semua impedansi bintang dibagi dengan impedansi bintang dari terminal yang sesuai sama dengan impedansi delta yang terhubung dengan terminal yang berlawanan.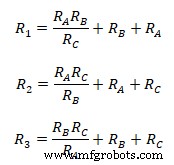 Jika semua impedansi bintang sama, impedansi delta ekivalennya adalah;
Jika semua impedansi bintang sama, impedansi delta ekivalennya adalah; Persamaan ini menunjukkan bahwa setiap impedansi delta ekivalen sama dengan 3 kali impedansi bintang.
Persamaan ini menunjukkan bahwa setiap impedansi delta ekivalen sama dengan 3 kali impedansi bintang.