Konversi Dari Penomoran Desimal

Karena sistem bilangan oktal dan heksadesimal memiliki basis yang merupakan kelipatan biner (basis 2), konversi bolak-balik antara heksadesimal atau oktal dan biner sangat mudah.

Juga, karena kita sudah sangat familiar dengan sistem desimal, mengubah biner, oktal, atau heksadesimal ke bentuk desimal relatif mudah (cukup menjumlahkan produk dari nilai sandi dan bobot tempat).

Namun, konversi dari desimal ke salah satu dari sistem penomoran "aneh" ini adalah masalah yang berbeda.

Metode Uji Coba

Metode yang mungkin paling masuk akal adalah metode "trial-and-fit", di mana Anda mencoba untuk "mencocokkan" notasi biner, oktal, atau heksadesimal ke nilai yang diinginkan seperti yang direpresentasikan dalam bentuk desimal.

Sebagai contoh, katakanlah saya ingin mewakili nilai desimal 87 dalam bentuk biner. Mari kita mulai dengan menggambar bidang bilangan biner, lengkap dengan nilai bobot tempat:

Yah, kita tahu bahwa kita tidak akan memiliki bit "1" di tempat 128, karena itu akan segera memberi kita nilai lebih besar dari 87.

Namun, karena bobot berikutnya ke kanan (64) kurang dari 87, kita tahu bahwa kita harus memiliki "1" di sana.

Jika kita juga membuat tempat berikutnya di sebelah kanan menjadi “1”, nilai total kita akan menjadi 64₁₀ + 32₁₀ , atau 96₁₀ . Ini lebih besar dari 87₁₀ , jadi kita tahu bahwa bit ini harus berupa “0”.

Jika kita membuat tempat berikutnya (16) sama dengan “1”, maka nilai total kita menjadi 64₁₀ + 16₁₀ , atau 80₁₀ , yang lebih mendekati nilai yang kita inginkan (87₁₀ ) tanpa melebihinya:

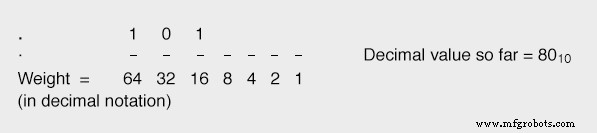
Dengan melanjutkan progresi ini, menetapkan setiap bit dengan bobot lebih rendah sesuai kebutuhan untuk mencapai nilai total yang diinginkan tanpa melebihinya, pada akhirnya kita akan sampai pada angka yang benar:

Metode Trial-and-Fit dalam Oktal dan Heksadesimal

Strategi uji coba ini akan bekerja dengan konversi oktal dan heksadesimal juga. Mari kita ambil angka desimal yang sama, 87₁₀ , dan ubah menjadi bilangan oktal:

Jika kita menempatkan sandi “1” di tempat 64, kita akan memiliki nilai total 64₁₀ (kurang dari 87₁₀ ). Jika kita menempatkan sandi “2” di tempat 64, kita akan memiliki nilai total 128₁₀ (lebih besar dari 87₁₀ ). Ini memberitahu kita bahwa penomoran oktal kita harus dimulai dengan "1" di tempat 64:

Sekarang, kita perlu bereksperimen dengan nilai cipher di tempat 8 untuk mencoba dan mendapatkan nilai total (desimal) sedekat mungkin dengan 87 tanpa melebihinya. Mencoba beberapa opsi cipher pertama, kami mendapatkan:

Nilai sandi "3" di tempat 8 akan menempatkan kita di atas total yang diinginkan 87₁₀ , jadi “2” itu!

Tentu saja, jika Anda memperhatikan selama bagian terakhir tentang konversi oktal/biner, Anda akan menyadari bahwa kita dapat mengambil representasi biner dari (desimal) 87₁₀ , yang sebelumnya kami tentukan sebagai 1010111₂ , dan dengan mudah mengkonversi dari itu ke oktal untuk memeriksa pekerjaan kami:

Bisakah kita melakukan konversi desimal ke heksadesimal dengan cara yang sama? Tentu, tapi siapa yang mau? Metode ini sederhana untuk dipahami, tetapi sulit untuk dilakukan.

Ada cara lain untuk melakukan konversi ini, yang pada dasarnya sama (secara matematis), tetapi lebih mudah dilakukan.

Teknik pembagian ulang

Metode lain ini menggunakan siklus pembagian berulang (menggunakan notasi desimal) untuk memecah penomoran desimal menjadi kelipatan nilai bobot tempat biner, oktal, atau heksadesimal.

Pada siklus pertama pembagian, kita mengambil bilangan desimal asli dan membaginya dengan basis sistem bilangan yang kita ubah (biner=2 oktal=8, hex=16).

Kemudian, kita mengambil bagian bilangan bulat dari hasil pembagian (bagi) dan membaginya dengan nilai dasar lagi, dan seterusnya, sampai kita mendapatkan hasil bagi kurang dari 1.

Digit biner, oktal, atau heksadesimal ditentukan oleh “sisa” yang tersisa dari setiap langkah pembagian. Mari kita lihat cara kerjanya untuk biner, dengan contoh desimal 87₁₀ :

Bit biner dirakit dari sisa langkah pembagian berturut-turut, dimulai dengan LSB dan melanjutkan ke MSB. Dalam hal ini, kita sampai pada notasi biner 1010111₂ .

Ketika kita membagi dengan 2, kita akan selalu mendapatkan hasil bagi yang diakhiri dengan ".0" atau ".5", yaitu sisa dari 0 atau 1. Seperti yang telah dikatakan sebelumnya, teknik pembagian ulang untuk konversi ini akan berfungsi untuk penomoran sistem selain biner.

Jika kita melakukan pembagian berturut-turut menggunakan angka yang berbeda, seperti 8 untuk konversi ke oktal, kita pasti akan mendapatkan sisa antara 0 dan 7. Mari kita coba ini dengan angka desimal yang sama, 87₁₀ :

Kita juga dapat menggunakan teknik serupa untuk mengonversi sistem penomoran yang berhubungan dengan jumlah yang kurang dari 1.

Untuk mengonversi bilangan desimal kurang dari 1 menjadi biner, oktal, atau heksadesimal, kita menggunakan perkalian berulang, dengan mengambil bagian bilangan bulat dari produk di setiap langkah sebagai digit berikutnya dari bilangan yang dikonversi.

Mari kita gunakan angka desimal 0,8125₁₀ sebagai contoh, konversi ke biner:

Seperti proses pembagian berulang untuk bilangan bulat, setiap langkah memberi kita digit (atau bit) berikutnya lebih jauh dari "titik".

Dengan bilangan bulat (pembagian), kami bekerja dari LSB ke MSB (kanan-ke-kiri), tetapi dengan perkalian berulang, kami bekerja dari kiri ke kanan.

Untuk mengonversi bilangan desimal yang lebih besar dari 1, dengan komponen <1, kita harus menggunakan keduanya teknik, satu per satu. Ambil contoh desimal dari 54.40625₁₀ , konversi ke biner:

LEMBAR KERJA TERKAIT:

• Lembar Kerja Sistem Penomoran