Teorema Superposisi digunakan untuk memecahkan jaringan yang kompleks dengan sejumlah sumber energi. Ini adalah konsep penting untuk menentukan tegangan dan arus melintasi elemen dengan menghitung efek masing-masing sumber secara individual. Dan gabungkan efek dari semua sumber untuk mendapatkan tegangan dan arus aktual dari elemen rangkaian.
Teorema superposisi menyatakan bahwa;
Dengan kata lain, kami akan mempertimbangkan hanya satu sumber independen yang bertindak pada satu waktu. Jadi, kita perlu menghapus sumber lain. Sumber tegangan dihubung pendek dan sumber arus dihubung terbuka untuk sumber ideal. Jika resistansi internal sumber diberikan, Anda perlu mempertimbangkan rangkaiannya.
Teorema superposisi hanya diterapkan pada rangkaian yang mengikuti hukum Ohm.
Jaringan harus mengikuti persyaratan di bawah ini untuk menerapkan teorema superposisi.
Langkah-1 Temukan sejumlah sumber independen yang tersedia di jaringan.
Langkah-2 Pilih salah satu sumber dan hilangkan semua sumber lainnya. Jika jaringan terdiri dari sumber dependen, Anda tidak dapat menghilangkannya. Tetap seperti itu selama perhitungan.
Jika Anda menganggap semua sumber energi adalah sumber ideal, Anda tidak perlu mempertimbangkan resistansi internal. Dan langsung sumber tegangan hubung singkat dan sumber arus hubung terbuka. Tetapi jika resistansi internal sumber diberikan, Anda harus mengganti resistansi internal.
Langkah-3 Sekarang, di sebuah sirkuit, hanya ada satu sumber energi independen. Anda perlu menemukan respons dengan hanya satu sumber energi di sirkuit.
Langkah-4 Ulangi langkah-2 dan 3 untuk semua sumber energi yang tersedia di jaringan. Jika ada tiga sumber independen, Anda perlu mengulangi langkah-langkah ini tiga kali. Dan setiap kali Anda mendapatkan beberapa nilai dari tanggapan tersebut.
Langkah-5 Sekarang, gabungkan semua respons dengan penjumlahan aljabar yang diperoleh dari sumber individual. Dan Anda akan mendapatkan nilai respons akhir untuk elemen jaringan tertentu. Jika Anda perlu menemukan respons untuk elemen lain, Anda perlu mengikuti langkah-langkah ini lagi untuk elemen tersebut.
Contoh:
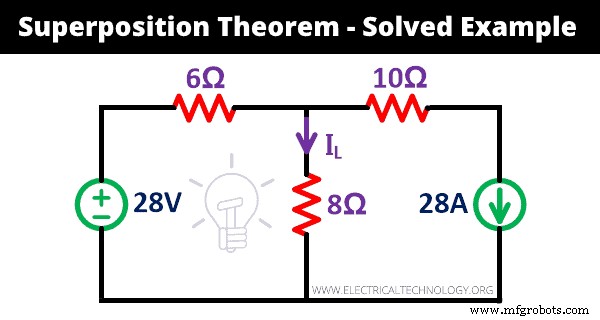
Mari kita pahami cara kerja teorema superposisi dengan contoh. Temukan arus (IL ) melewati resistor 8Ω di jaringan yang diberikan menggunakan teorema superposisi.
Solusi:
Langkah-1 Seperti yang ditunjukkan pada jaringan di atas, satu sumber tegangan, dan satu sumber arus diberikan. Oleh karena itu, kita perlu mengulangi prosedur ini dua kali.
Langkah-2 Pertama kami mempertimbangkan sumber tegangan 28V hadir di jaringan. Jadi, Anda perlu menghapus sumber arus dengan terminal sirkuit terbuka. Seperti di sini, kami menganggap sumber arus sebagai sumber arus yang ideal. Jadi, kita tidak perlu menghubungkan resistansi internal.
Sirkuit yang tersisa adalah seperti yang ditunjukkan pada gambar di bawah ini.
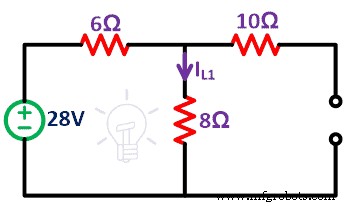
Langkah-3 Temukan arus (IL1 ) melewati resistor 8Ω. Ini hanya memberikan efek sumber tegangan.
Karena rangkaian terbuka dari sumber arus, tidak ada arus yang melewati resistor 10Ω. Jadi, jaringan hanya terdiri dari satu loop.
Terapkan KVL ke loop;
28 =6Saya L 1 + 8Saya L 1
28 =14Saya L 1
Saya L 1 =28/14
Saya L 1 =2A
Langkah-4 Sekarang, kita ulangi prosedur yang sama untuk sumber saat ini. Dalam kondisi ini, kami menghapus sumber tegangan dengan hubungan arus pendek. Sirkuit yang tersisa adalah seperti yang ditunjukkan pada gambar di bawah ini.
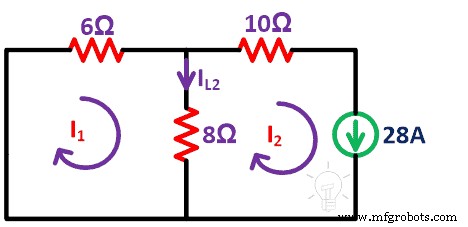
Di sini, kita harus mempertimbangkan dua loop. Saya1 dan saya2 adalah arus loop. Dan temukan IL2 current saat ini .
Terapkan KVL ke loop-1;
0 =6Saya 1 + 8Saya 1 – 8Saya 2
14Saya 1 – 8Saya 2 =0
Arus yang melewati loop-2 dihitung dari sumber saat ini. Dan itu akan menjadi;
Saya 2 =28A
Masukkan nilai ini ke dalam persamaan di atas;
14Saya 1 – 8 (28) =0
Saya 1 =16A
Sekarang, cabang resistor 8Ω umum di kedua loop. Jadi, kita perlu mencari arus yang dihasilkan (IL2 ) melewati resistor 8Ω.
Saya L 2 =Saya 1 – Saya 2
Saya L 2 =16 – 28
Saya L 2 =-12A
Langkah-5 Sekarang, kami menggabungkan efek dari kedua sumber dengan penjumlahan aljabar arus. Jadi, arus total yang melewati resistor 8Ω adalah IL . Di sini, arah arus paling penting. Saat ini sayaL2 memiliki tanda minus. Artinya selama sumber 28A, arus mengalir dalam arah yang berlawanan. Dan kita tidak bisa mengubah arah. Itulah alasannya saat menggabungkan semua sumber, kami melakukan penjumlahan aljabar.
Saya L =SayaL 1 – SayaL 2
Saya L =2 + (-12)
Saya L =-10A
Di sini, kita mengasumsikan bahwa arus yang melewati resistor 8Ω searah dengan panah yang ditunjukkan pada gambar. Tanda minus menunjukkan arah yang berlawanan. Dan besarnya arus adalah 8A.
Eksperimen teorema superposisi dapat dilakukan dengan mengikuti langkah-langkah di bawah ini.
Tujuan
Tentukan arus yang mengalir melalui resistor dan verifikasi teorema superposisi.
Komponen yang Diperlukan
Sumber DC, Resistor, multimeter DC, Kabel Penghubung, Breadboard, dll.
Teori
Teorema superposisi digunakan dalam analisis rangkaian untuk menemukan arus dan tegangan melintasi elemen dalam rangkaian tertentu. Teorema ini berguna ketika jumlah sumber lebih banyak.
Menurut teorema superposisi, respons elemen adalah penjumlahan aljabar respons dari sumber energi individu.
Pertama, kita akan menghitung arus yang melewati resistor di jaringan tertentu. Ketika semua sumber terhubung. Setelah itu, kami menghapus sumber dan menemukan arus untuk masing-masing sumber. Akhirnya, penjumlahan arus yang diukur dari masing-masing sumber serupa dengan pengukuran arus dengan semua sumber terhubung.
Prosedur
Kami mempertimbangkan sirkuit bilateral linier yang diberikan pada gambar di bawah ini.
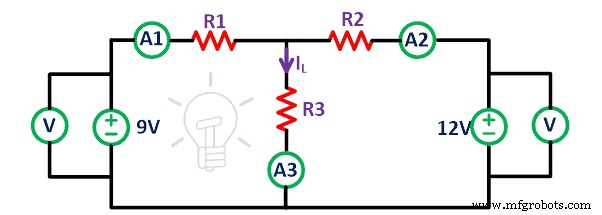
Hubungkan semua elemen pada papan tempat memotong roti seperti yang diberikan pada rangkaian di atas menggunakan kabel penghubung. Hubungkan ammeter dengan semua resistor untuk menemukan arus yang melewati resistor. Di sini, kami memiliki dua sumber tegangan.
Dalam kasus pertama, ukur arus yang melewati semua resistor ketika kedua sumber tegangan ada di sirkuit. Arus yang mengalir melalui resistor R1 , R2 , dan R3 adalah Saya 1 , Saya 2 , dan Saya 3 masing-masing.
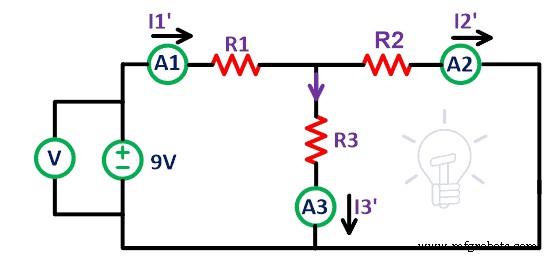
Sekarang lepaskan sumber tegangan 12V dari rangkaian. Pendek terminal A' dan B' seperti yang ditunjukkan pada gambar di atas. Di sini kita mengasumsikan bahwa sumber tegangan ideal. Jadi, tidak perlu menghubungkan resistansi internal. Sekarang, ukur arus I 1′ , Saya 2′ dan Saya 3′ yang merupakan arus yang melewati resistor R1, R2, dan R3 masing-masing.
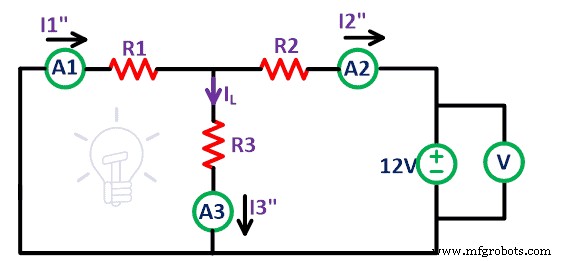
Demikian pula, lepaskan sumber tegangan 9V dan rangkaian yang tersisa seperti yang ditunjukkan pada gambar di atas. Sekali lagi, ukur arus yang mengalir melalui semua resistor dan beri nama I 1 “ , Saya 2 “ , dan Saya 3 “ .
Masukkan semua nilai pada tabel observasi di bawah ini.
Tabel Pengamatan
| Koneksi Sumber | R1 | R2 | R3 |
| Kedua sumber terhubung | Saya 1 | Saya 2 | Saya 3 |
| Hanya 12V yang terhubung | Saya 1′ | Saya 2′ | Saya 3′ |
| Hanya 9V yang terhubung | Saya 1″ | Saya 2″ | Saya 3″ |
Perhitungan :
Saya 1 =Saya 1′ + Saya 1″
Saya 2 =Saya 2′ + Saya 2″
Saya 3 =Saya 3′ + Saya 3″
Untuk memverifikasi teorema superposisi, kami membandingkan penjumlahan aljabar arus yang melewati resistor ketika satu sumber dihubungkan dengan arus yang diukur ketika kedua sumber dihubungkan dalam suatu rangkaian.
Jika perhitungan di atas memenuhi, kita dapat membuktikan teorema superposisi.
Kesimpulan
Dalam percobaan ini, kita dapat membuktikan bahwa arus yang melewati hambatan adalah penjumlahan aljabar arus ketika sumber energi individu dihubungkan. Dan ini membuktikan teorema superposisi.
Tutorial Analisis Rangkaian Listrik Terkait:
Teknologi Industri
Menganalisis &Menyelesaikan Rangkaian Listrik Menggunakan Teorema Substitusi Teorema Substitusi Seperti namanya, teorema substitusi digunakan untuk mengganti satu elemen rangkaian dengan elemen lain. Namun saat mengganti elemen, Anda harus ingat bahwa perilaku rangkaian tidak boleh berubah. Teorema
Perlu waktu terlalu lama untuk memindahkan inventaris dari penyimpanan ke pengiriman. Dibutuhkan pekerja terlalu lama untuk mengidentifikasi rak yang tepat dan memilih inventaris. Pekerja ditahan menunggu karyawan lain selesai mengambil inventaris dari area yang sama. Kemacetan lalu lintas sering te
Tentang Sirkuit Dengan Energi Gratis，Bisakah kita mendapatkan energi secara gratis? Bagaimana kita bisa mendapatkan listrik, dan apakah ada cara untuk menyimpan listrik yang kita kumpulkan? Di bawah ini, kita akan melihat perangkat yang dapat merasakan dan menangkap pita energi di sekitar kita. Si
Tidaklah bagus ketika air merusak sirkuit yang telah Anda kerjakan selama beberapa waktu. Dan, lebih menyebalkan lagi jika perangkat yang membutuhkan perlindungan dari air atau hujan terluka. Untungnya, kami punya solusinya. Sirkuit sensor air adalah semua yang Anda butuhkan. Sirkuit sensor air juga
