Teorema Tellegen – Contoh Soal &Simulasi MATLAB

Teorema Tellegen – Panduan Langkah demi Langkah dengan Contoh Selesai

Apa itu Teorema Tellegen?

Teorema Tellen diterbitkan oleh seorang insinyur dan penemu listrik Belanda Bernard D.H. Tellegen pada tahun 1952. Teorema ini merupakan teorema yang paling penting dan mendasar di antara teorema lain dalam analisis jaringan. Sebagian besar teorema lain diturunkan dari teorema ini.

Teorema Tellegen bergantung pada hukum Kirchhoff. Oleh karena itu, teorema ini dapat diterapkan pada jaringan yang mematuhi hukum Kirchhoff. Teorema ini dapat diterapkan pada berbagai jaringan yang memiliki elemen linier atau nonlinier, varian waktu atau nonvarian, pasif atau aktif.

Teorema Tellegen menyatakan bahwa;

Teorema Tellegen bekerja berdasarkan prinsip hukum kekekalan energi. Teorema ini digunakan dalam aplikasi kimia dan biologi untuk menemukan perilaku dinamis dari jaringan fisik. Dalam pemrosesan sinyal, teorema ini digunakan untuk merancang filter.

• Postingan Terkait:Teorema Thevenin. Panduan Langkah demi Langkah dengan Contoh Terpecahkan

Persamaan Matematika

Untuk analisis umum teorema, kami menganggap jumlah elemen 'n' diberikan dalam jaringan. Arus sesaat yang melewati elemen adalah i₁ , i₂ , i₃ , …., i_n . Dan tegangan sesaat dari cabang ini adalah v₁ , v₂ , v₃ , …., v_n .

Oleh karena itu, arus dan tegangan sesaat elemen-1 adalah i₁ dan v₁ . Kekuatan sesaat (p₁ ) yang dikonsumsi oleh elemen ini adalah v₁ i₁ .

p ₁ =v ₁ saya ₁

Kekuatan sesaat elemen-2 adalah (p ₂ );

p ₂ =v ₂ saya ₂

Demikian pula, kekuatan sesaat dari n ^th elemennya adalah (p _n );

p_n =v_n saya_n

Menurut teorema Tellegen, penjumlahan semua daya sesaat adalah nol. Itu berarti kita perlu menjumlahkan semua daya sesaat p₁ , p₂ , p₃ , …., p_n .

p ₁ + p ₂ + p ₃ + … + p_n = 0

v ₁ saya ₁ + v ₂ saya ₂ + v ₃ saya ₃ + … + v_n saya_n  = 0

Dalam bentuk umum, kita dapat menulis persamaan di atas untuk k ^th cabang;

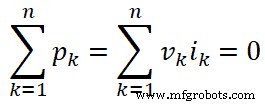
Di mana,

• n =jumlah total cabang dalam jaringan
• v_k =tegangan sesaat k ^th cabang
• i_k =arus sesaat k ^th cabang
• p_k =kekuatan sesaat k ^th cabang

Sekarang, perhatikan gambar di bawah ini karena cabang AB sama dengan cabang k.

Oleh karena itu, tegangan sesaat v_k ;

v_k =v_a – v_b

Dan arus sesaat yang melewati cabang (a ke b) adalah i_k ;

i_k =i_ab

Jadi, kekuatan sesaat p_k adalah;

p_k =v_k saya_k =(v_a – v_b ) i_ab ….. (1)

Sekarang, kita perhatikan arah berlawanan dari arus sesaat (b ke a);

i_ab =– i_ab

Tegangan sesaat;

v_k =v_b – v_a

Kekuatan sesaat p_k adalah;

p_k =v_k saya_k =(v_b – v_a ) saya_ba ….. (2)

Penjumlahan persamaan-1 dan 2;

2v_k saya_k =(v_a –v _b ) aku _ab + (v_b – v_a ) i_ba

v_k saya_k =1/2 [(v_a –v _b ) aku _ab + (v_b – v_a ) i_ba ] ….. (3)

Persamaan ini dapat ditulis seperti di bawah ini untuk n-branch;

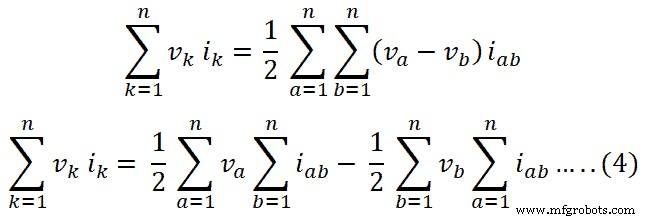
Menurut hukum Kirchhoff saat ini, penjumlahan aljabar arus adalah nol pada simpul rangkaian.

Oleh karena itu,

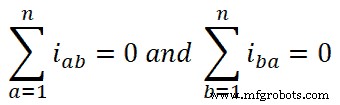
Jika kita memasukkan nilai ini ke dalam persamaan-4, kita memperoleh;

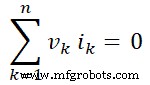
Dengan demikian, terbukti bahwa penjumlahan daya yang dikirimkan ke jaringan adalah nol. Oleh karena itu, teorema Tellegen terbukti. Dijelaskan juga bahwa jumlah daya yang diserap oleh elemen jaringan sama dengan jumlah daya yang dikirimkan oleh sumber.

• Postingan Terkait: Teorema Norton. Panduan Langkah demi Langkah dengan Contoh Terpecahkan

Langkah-Langkah yang Harus Diikuti untuk Teorema Tellegen

Kita perlu mengikuti langkah-langkah di bawah ini untuk menyelesaikan jaringan listrik apa pun dengan teorema Tellegen.

Langkah-1: Kita perlu menemukan sejumlah cabang di jaringan listrik yang diberikan. Kemudian temukan daya yang hilang di setiap cabang. Untuk menemukan daya, kita perlu mencari tegangan atau arus dari cabang tersebut menggunakan metode analisis konvensional.

Langkah-2: Temukan kekuatan sesaat dari setiap cabang.

Langkah-3: Cabang yang memiliki sumber energi dianggap sebagai cabang pemberi tenaga. Dan cabang yang memiliki unsur lain dianggap sebagai cabang penyerap tenaga. Sekarang kenali cabang pemberi daya dan cabang penyerap daya.

Langkah-4: Asumsikan tanda positif pada cabang penghantar daya dan penurunan tegangan negatif pada cabang penyerap daya. Anda dapat mengasumsikan tanda-tanda terbalik juga. Tetapi tidak dapat mengubah seluruh contoh.

Langkah-5: Untuk membenarkan teorema Tellegen, kita perlu menambahkan semua kekuatan yang dihitung dari semua cabang. Dan penjumlahan ini selalu nol.

• Postingan Terkait: Analisis Sirkuit SUPERMESH – Langkah demi Langkah dengan Contoh Terpecahkan

Mari kita pahami dengan sebuah contoh.

Contoh Pemecahan Teorema Tellegen

Contoh #1

Membenarkan teorema Tellegen untuk jaringan di bawah ini.

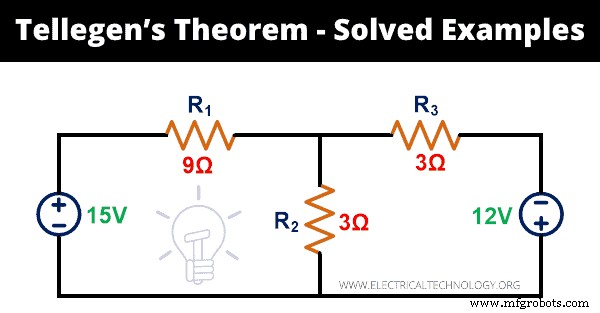
Solusi:

Langkah-1: Jaringan sirkuit yang diberikan memiliki 5 cabang. Untuk menghitung daya sesaat, kita perlu mencari arus yang melewati setiap cabang. Untuk itu, kami akan menerapkan KVL ke jaringan.

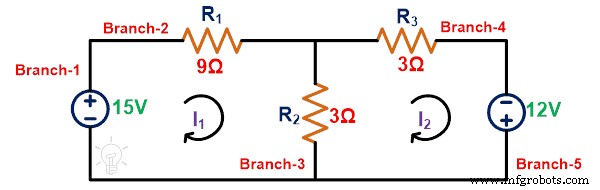
Terapkan KVL ke loop-1;

15 =12Saya ₁ – 3Saya ₂

Terapkan KVL ke loop-2;

12 =– 3Saya ₂ + 6Saya ₂

Dengan menyelesaikan persamaan di atas, kita dapat menemukan nilai arus loop I₁ dan saya₂ . Dan nilai-nilai ini adalah;

Saya ₁ =2A

Saya ₂ =3A

Langkah-2: Arus yang melalui cabang-3 adalah;

Saya _{1 2} =Saya ₂ – Saya ₁ =3 – 2 =1A

Kami memiliki arus yang mengalir melalui semua cabang. Sekarang, temukan kekuatan setiap cabang.

P ₁ =V I ₁ =15 x 2 =30W

P ₂ =R ₁ Saya ₁ ² =9 x 4 =36W

P ₃ =R ₁ Saya ₁₂ ² =3 x 1 =3W

P ₄ =R ₃ Saya ₂ ² =3 x 9 =27W

P ₅ =V I ₂ =12 x 3 =36W

Langkah-3: Ada dua cabang yang memiliki sumber. Cabang-cabang ini adalah cabang pemberi daya dan tiga cabang lainnya adalah cabang penyerap daya.

Di sini, untuk contoh ini, kita asumsikan bahwa tanda cabang pemberi daya adalah positif dan tanda cabang penyerap daya adalah negatif. Oleh karena itu, cabang-1 dan 5 adalah cabang pemberi daya dan cabang lainnya adalah cabang penyerap daya.

Langkah-4: Tanda kekuatan P₁ dan P₅ positif (cabang yang memberikan kekuatan) dan tanda P₂ , P₃ , dan P₄ negatif (cabang penyerap daya).

Langkah-5: Sekarang, kita perlu menemukan penjumlahan daya yang dihamburkan oleh semua cabang.

P ₁ – P ₂ – P ₃ – P ₄ + P ₅ =30W – 36W – 3W – 27W + 36W =0W

Jadi, penjumlahan daya sesaat adalah nol. Dan karenanya, teorema ini terbukti.

• Postingan Terkait:Analisis Rangkaian SUPERNODE – Langkah demi Langkah dengan Contoh Selesai

Contoh #2

Temukan tegangan pada sumber arus 6A menggunakan teorema Tellegen.

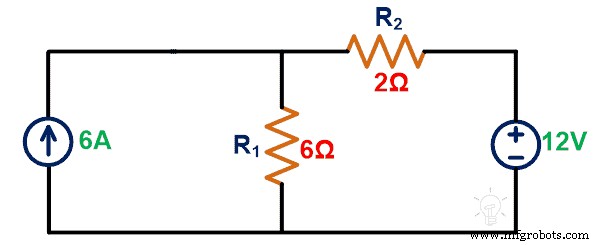
Solusi:

Langkah-1: Kita perlu menghitung tegangan atau arus yang melewati elemen tersebut. Untuk itu, kami menerapkan KCL atau KVL ke jaringan yang diberikan.

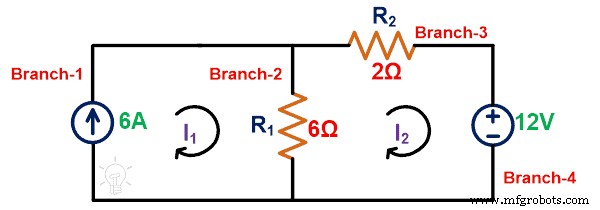
Terapkan KVL ke loop-2;

-12 =8Saya ₂ – 6Saya ₁

Arus yang melewati cabang yang memiliki sumber arus adalah I ₁;

Saya ₁ =6A

Masukkan nilai ini ke dalam persamaan di atas;

-12 =8Saya ₂ – 6(6)

-12 =8Saya ₂ – 36

36 – 12 =8Saya ₂

24 =8Saya ₂

Saya ₂ =3A

Langkah-2: Arus yang melalui cabang-2 adalah;

Saya ₁₂ =Saya ₁ – Saya ₂ =6 – 3 =3A

Sekarang, temukan kekuatan setiap cabang;

P ₁ =V I ₁ =V x 6 =6 x V

P ₂ =R ₁ Saya ₁₂ ² =6 x 9 =54W

P ₄ =R ₂ Saya ₂ ² =2 x 9 =18W

P ₄ =V I ₂ =-12 x 3 =-36W

Langkah-3: Di sini, dua cabang memiliki sumber energi. Oleh karena itu, kita harus mempertimbangkan cabang-cabang ini sebagai cabang pemberi kekuatan. Dan atur tanda positif ke kekuatan sesaat.

Dua cabang lainnya hanya memiliki resistor. Jadi, cabang-cabang ini adalah cabang penyerap kekuatan dan mengatur tanda negatif ke kekuatan sesaat.

Langkah-4: Daya P₁ dan P₄ memiliki tanda positif dan pangkat P₂ dan P3 bertanda negatif.

Langkah-5: Sekarang, kita perlu menjumlahkan semua kekuatan sesaat.

P ₁ – P ₂ – P ₃ + P ₄ =0W

P ₁ – 54 – 18 + 36 =108W

Daya yang dikirimkan oleh sumber arus 6A adalah 108W. Oleh karena itu, tegangan pada sumber arus dihitung dengan;

P ₁ =V I

108W =V x 6A

V =18V

Oleh karena itu, tegangan pada sumber arus adalah 18V.

• Pos Terkait: Teorema Transfer Daya Maksimum untuk Sirkuit AC &DC

Analisis &Simulasi Teorema Tellegen Menggunakan MATLAB  

Tujuan:

Buktikan Teorema Tellegen untuk diagram rangkaian yang diberikan dalam contoh di atas.

Persyaratan: MATLAB

Teori:

Menurut teorema Tellegen, penjumlahan pangkat semua cabang sama dengan nol. Untuk membuktikan teorema ini, kita perlu menghitung kekuatan sesaat dari semua cabang.

Untuk mencari daya sesaat, kita perlu menghitung tegangan atau arus semua cabang. Untuk itu, kita dapat menggunakan teorema KCL atau KVL. Namun disini kita akan menggunakan model MATLAB Simulink untuk mencari arus dan tegangan.

Kita juga bisa menggunakan software lain seperti multisim, psim, dll. Kita akan membuat diagram rangkaian dalam model Simulink. Dengan model Simulink, Anda dapat menemukan tegangan dan arus setiap cabang.

Setelah itu, Anda dapat menemukan daya sesaat dari tegangan dan arus. Anda dapat langsung menemukan kekuatan sesaat dari beberapa perangkat lunak.

Model Simulink MATLAB

Gambar di bawah menunjukkan diagram rangkaian dari contoh di atas.

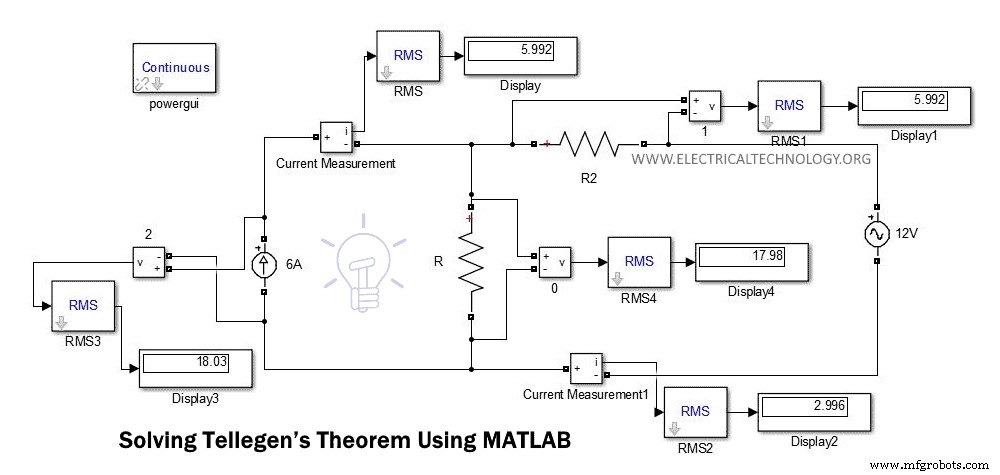
Pada gambar ini, kita dapat langsung menemukan tegangan dan arus dari tampilan. Anda dapat membandingkan nilai ini dengan menghitung tegangan dan arus dengan bantuan KCL atau KVL.

Perhitungan

Setelah menghitung tegangan atau arus, Anda dapat menemukan daya sesaat. Atau Anda dapat langsung menemukan kekuatan instan dari perangkat lunak. Yang kita butuhkan hanyalah kekuatan sesaat. Dan setelah itu, kita perlu menambahkan semua kekuatan.

Penjumlahan pangkat selalu nol. Untuk contoh ini, kami membandingkan nilai tegangan dan arus yang ditemukan dari Simulink dan nilai yang sama yang dihitung pada contoh sebelumnya menggunakan KVL dan KCL. Nilai-nilai ini sama.

Nilai ini juga dihitung oleh resistor penghubung dan sumber pada papan tempat memotong roti. Dan kita dapat mengukur tegangan dan arus yang melewati semua cabang dengan bantuan voltmeter dan ammeter.

Dengan demikian, teorema Tellegen terbukti.

• Postingan Terkait:Hukum Arus &Tegangan Kirchhoff (KCL &KVL) | Contoh yang Diselesaikan

Penerapan Teorema Tellegen

Teorema ini sangat mendasar dan banyak digunakan dalam analisis rangkaian. Ada banyak aplikasi teorema ini. Beberapa aplikasi tercantum di bawah ini.

• Untuk mendesain filter, teorema ini sangat berguna dalam aplikasi pemrosesan sinyal digital.
• Untuk menentukan stabilitas pabrik kimia, teorema ini digunakan dalam teknik kimia.
• Teorema ini berlaku untuk sistem gabungan yang memiliki elemen linear-nonlinier, aktif-pasif, varian waktu/waktu-invarian.
• Teorema ini digunakan dalam proses biologis.
• Ini digunakan dalam topologi dan analisis reaksi struktur.
• Ini juga digunakan untuk menemukan perilaku dinamis jaringan fisik.

Tutorial Analisis Rangkaian Listrik Terkait:

• Teorema Superposisi – Analisis Rangkaian dengan Contoh Selesai
• Kalkulator Aturan Cramer – Sistem Persamaan 2 dan 3 untuk Rangkaian Listrik
• Jembatan Wheatstone – Sirkuit, Kerja, Derivasi, dan Aplikasi
• Kalkulator Teknik Elektro dan Elektronik
• 5000+ Rumus &Persamaan Teknik Elektro dan Elektronik