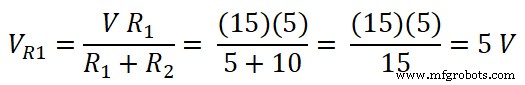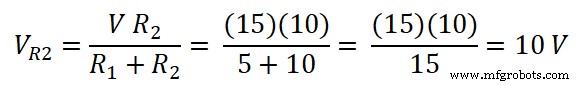Teorema Substitusi – Panduan Langkah demi Langkah dengan Contoh Selesai
Menganalisis &Menyelesaikan Rangkaian Listrik Menggunakan Teorema Substitusi
Teorema Substitusi
Seperti namanya, teorema substitusi digunakan untuk mengganti satu elemen rangkaian dengan elemen lain. Namun saat mengganti elemen, Anda harus ingat bahwa perilaku rangkaian tidak boleh berubah.
Teorema substitusi menyatakan bahwa;
Teorema ini digunakan untuk membuktikan beberapa teorema. Untuk mengganti cabang jaringan, teorema ini memberi tahu kita kondisi batas.
Jika nilai arus yang melewati cabang dan nilai tegangan yang melintasi cabang diketahui, kita dapat mengganti cabang ini dengan elemen lain seperti sumber tegangan, sumber arus, berbeda nilai resistor, dll. dengan melakukan ini, kondisi awal tetap tidak berubah.
Teorema ini tidak dapat diterapkan jika rangkaian memiliki lebih dari dua sumber yang dihubungkan secara seri atau paralel.
- Postingan Terkait: Teorema Thevenin. Panduan Langkah demi Langkah dengan Contoh Terpecahkan
Penjelasan Teorema Substitusi
Teorema substitusi adalah penggantian setiap cabang jaringan dengan cabang setara yang memiliki elemen berbeda. Dalam teorema ini, jika ada cabang atau elemen yang diganti dengan sumber tegangan dan arus yang sama dengan jaringan aslinya, maka tegangan dan arus cabang tersebut.
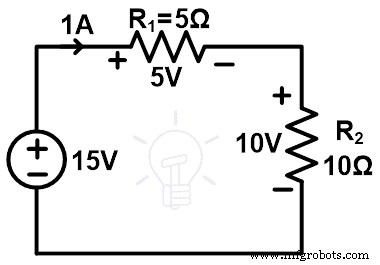
Mari kita pahami teorema substitusi dengan jaringan yang ditunjukkan pada gambar di bawah ini.
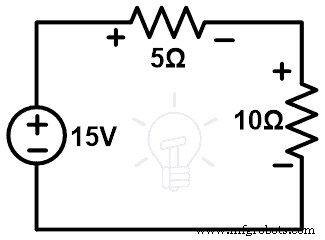
Seperti yang ditunjukkan pada gambar di atas, ia memiliki dua resistor yang dihubungkan secara seri dengan sumber DC. Sekarang, kami akan mencoba mengganti cabang atau elemen apa pun dengan elemen lain. Sebelum itu, kita perlu mengetahui tegangan dan arus yang melewati semua cabang.
Di sini, sirkuit ini hanya memiliki satu loop. Oleh karena itu, arus yang melewati semua cabang dan elemen adalah sama. Arus ini dapat ditentukan dengan menerapkan KVL ke jaringan.
Katakanlah, saya jumlah arus yang melewati loop.
+15 =5Saya + 10Saya
15 =15Saya
Saya =1A
Jadi, arus yang melewati setiap elemen adalah 1A. Sekarang, kita perlu mencari tegangan di semua elemen.
Satu cabang memiliki sumber tegangan. Jadi, kami tidak menemukan tegangan cabang itu. Tegangan ini terbagi menjadi dua resistor. Dan kita perlu menemukan tegangan di setiap resistor. Ini dapat ditemukan dengan menerapkan aturan pembagi tegangan.
Jadi, tegangan pada resistor 5Ω adalah;
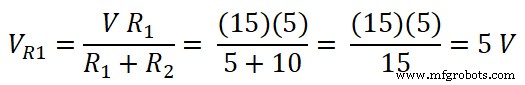
Demikian pula, tegangan pada resistor 10Ω adalah;
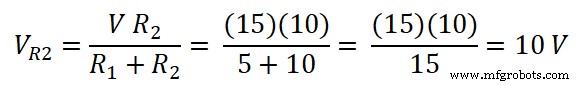
- Postingan Terkait: Teorema Norton. Panduan Langkah demi Langkah dengan Contoh Terpecahkan
Pengganti-1
Kita dapat mengganti cabang resistor 10Ω dengan sumber tegangan 10V seperti yang ditunjukkan pada gambar di bawah.
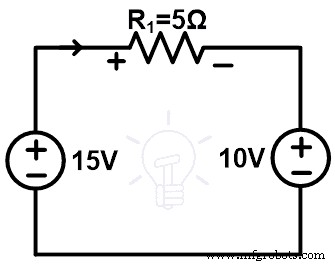
Sekarang, terapkan KVL ke jaringan,
+15 – 10 =5Saya
5 =5Saya
Saya =1A
Jadi, arus loop sama dengan rangkaian aslinya. Sekarang, hitung tegangan lintas elemen. Cabang resistor 10Ω diganti dengan sumber 10V. Oleh karena itu, tegangan di cabang itu adalah 10V. Dan tegangan ini sama dengan tegangan cabang itu di sirkuit aslinya.
Sekarang, cari tegangan pada cabang resistor 5Ω. Arus yang melalui cabang ini adalah 1A. Oleh karena itu, menurut hukum Ohm;
V 5Ω =1A × 5 =5V
Jadi, arus melewati semua cabang dan tegangan di semua cabang sama dengan jaringan aslinya.
Pengganti-2
Hapus cabang resistor 5Ω. Dan ganti cabang ini dengan sumber tegangan 5V. Diagram rangkaian substitusi ini seperti yang ditunjukkan pada gambar di bawah ini.
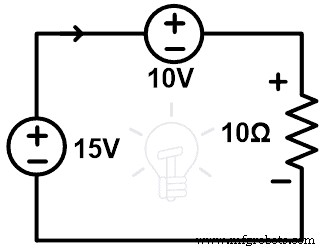
Sekarang, hitung arus dan tegangan semua cabang dan bandingkan dengan jaringan asli.
Untuk menemukan arus yang melewati loop, terapkan KVL;
+15 – 5 =10Saya
10 =10Saya
Saya =1A
Oleh karena itu, arus loop atau arus yang melewati elemen sama dengan arus yang melewati jaringan asli.
Cabang resistor 5Ω diganti dengan sumber tegangan 5V. Oleh karena itu, tegangan cabang ini sama dengan tegangan di jaringan asli. Sekarang, kita perlu menghitung tegangan pada cabang resistor 10Ω.
Arus yang melewati cabang resistor 10Ω adalah 1A. Menurut hukum Ohm;
V 10Ω =IR
V 10Ω =1 × 10
V 10Ω =+10 V
Jadi, setelah mengganti resistor 5Ω dengan sumber tegangan 5V, perilaku jaringan tidak berubah.
- Postingan Terkait: Teorema Superposisi – Analisis Rangkaian dengan Contoh Selesai
Pengganti-3
Lepaskan cabang resistor 10Ω dan ganti dengan sumber arus 1A. Diagram rangkaian setelah substitusi adalah seperti yang ditunjukkan pada gambar di bawah ini.
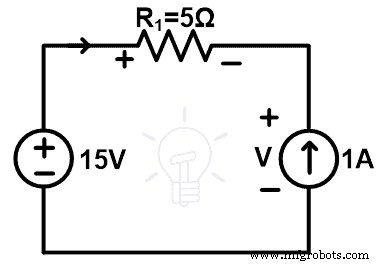
Ada sumber arus di sirkuit. Oleh karena itu, arus yang melewati loop sama dengan jumlah sumber arus. Dalam kondisi ini, sumber arus 1A terhubung ke jaringan. Dan karenanya, arus yang melewati loop adalah 1A yang sama dengan arus yang melewati jaringan asli.
Sekarang, hitung tegangan pada resistor 5Ω dan sumber arus 1A.
Menurut hukum Ohm,
V 5Ω =IR
V 5Ω =1 × 5
V 5Ω =+5 V
Sekarang, cari tegangan pada sumber arus 1A. Mari kita asumsikan tegangan pada sumber arus 1A adalah V.
Dari gambar di atas;
+15 – 5 – V =0
V =+10 V
Jadi, terbukti bahwa tegangan dan arus yang melewati semua elemen sama dengan jaringan aslinya setelah resistor 10Ω diganti dengan sumber arus 1A.
- Postingan Terkait:Teorema Millman – Menganalisis Rangkaian AC &DC – Contoh
Substitusi-4
Lepaskan cabang resistor 10Ω dan ganti dengan resistor 5Ω yang dihubungkan seri dengan sumber tegangan 5V. Diagram rangkaian pengganti ini seperti yang ditunjukkan pada gambar di bawah ini.
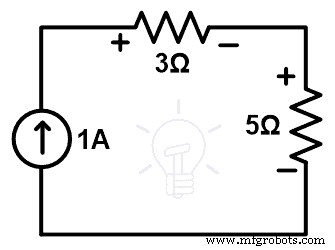
Sekarang, kita perlu menemukan arus yang melewati loop. Jadi, terapkan KVL ke jaringan di atas.
15 – 5 =5Saya + 5Saya
10 =10Saya
Saya =1A
Jadi, arus yang melewati elemen sama dengan jaringan aslinya. Sekarang, temukan tegangan di semua elemen.
Untuk mencari tegangan pada resistor 5Ω; kami menggunakan hukum Ohm.
V 5Ω =IR
V 5Ω =1 × 5
V 5Ω =5 V
Sekarang, kita cari tegangan di titik A dan B.
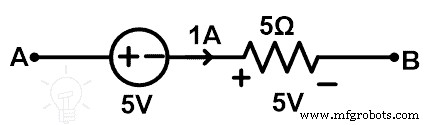
Dari gambar di atas, arus yang melewati resistor 5Ω adalah 1A. Jadi, tegangan pada elemen ini adalah 5V. Dan tegangan total antara titik A dan B adalah
V AB =5 + V 5Ω
V AB =5 + 5
V AB =+10V
Oleh karena itu, setelah penggantian cabang resistor 10Ω dengan resistor 5Ω dan sumber tegangan 5V, perilaku jaringan tetap sama.
Jadi, kita dapat mengatakan bahwa ada beberapa metode yang tersedia untuk menemukan substitusi elemen jaringan apa pun tanpa mengubah tegangan dan arus elemen dan tanpa mengubah perilaku elemen jaringan.
- Postingan Terkait: Teorema Tellegen – Contoh Soal &Simulasi MATLAB
Langkah-Langkah Menyelesaikan Jaringan Menggunakan Teorema Substitusi
Langkah-1 Temukan tegangan dan arus semua elemen jaringan. Umumnya, tegangan dan arus dapat dihitung dengan sederhana menggunakan hukum KCL, KVL, atau Ohm.
Langkah-2 Temukan cabang yang bersangkutan, yang ingin Anda hapus dengan elemen lain seperti sumber arus, sumber tegangan, atau hambatan.
Langkah-3 Temukan nilai elemen pengganti yang sesuai dengan ketentuan bahwa tegangan dan arus tidak boleh berubah.
Langkah-4 Verifikasi sirkuit baru dengan menghitung tegangan dan arus semua elemen. Dan bandingkan dengan jaringan aslinya.
Ini semua tentang teorema substitusi. Sekarang, mari kita ambil contoh.
- Pos Terkait: Teorema Transfer Daya Maksimum untuk Sirkuit AC &DC
Contoh &Solusi Teorema Substitusi
Pecahkan jaringan di bawah ini menggunakan teorema substitusi untuk menghitung arus dan tegangan di semua resistor.
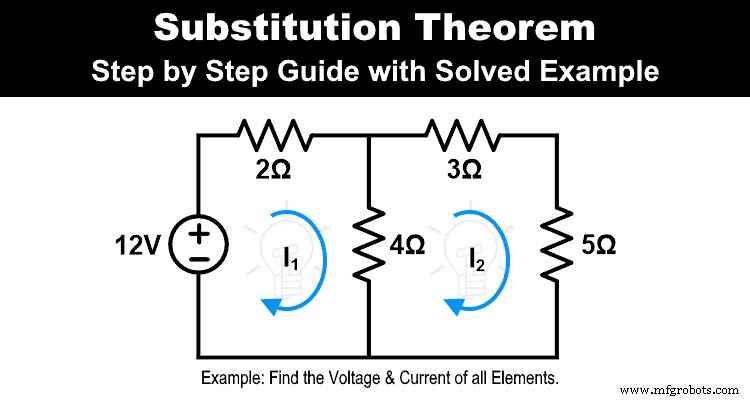
Langkah-1 Temukan tegangan dan arus semua elemen. Untuk itu, dalam contoh ini, kami menerapkan KVL ke jaringan.
Terapkan KVL pada loop-1;
14 =6Saya 1 – 4Saya 2 … (1)
Terapkan KVL pada loop-2;
0 =12Saya 2 – 4Saya 1
12Saya 2 =4Saya 1
Saya 1 =3Saya 2 … (2)
Masukkan nilai ini ke dalam persamaan-1;
14 =6(3Saya 2 ) – 4Saya 2
14 =18Saya 2 – 4Saya 2
14 =14Saya 2
Saya 2 =1A
Dari persamaan-2;
Saya 1 =3A
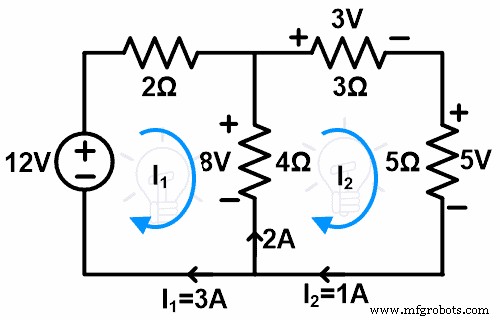
Langkah-2 Sekarang, kita akan menghapus cabang dari loop-1 dan membuat satu loop.
Langkah-3 Kita dapat menempatkan sumber tegangan atau sumber arus sebagai pengganti resistor 4Ω. Di sini, kami akan menempatkan sumber saat ini.
Arus yang melewati loop-2 adalah 1A. Oleh karena itu, kami mengganti cabang dengan sumber arus 1A. Jadi, rangkaian yang tersisa adalah seperti yang ditunjukkan pada gambar di bawah ini.

Langkah-4 Mari kita verifikasi tegangan dan arus semua elemen.
Jaringan ini memiliki satu loop. Dan loop ini memiliki sumber arus. Jadi, nilai arus yang melewati loop sama dengan nilai sumber arus.
Di sini, nilai sumber saat ini adalah 1A. Oleh karena itu, arus yang melalui cabang 3Ω dan cabang resistor 5Ω adalah 1A yang sama dengan jaringan aslinya.
Sekarang, cari tegangan pada resistor 3Ω menggunakan hukum Ohm;
V 3Ω =IR
V 3Ω =1 x 3
V 3Ω =3V
Sekarang, cari tegangan pada resistor 5Ω menggunakan hukum Ohm;
V 5Ω =IR
V 5Ω =1 x 5
V 5Ω = 5V
Jadi, tegangan dan arusnya sama dengan jaringan aslinya. Beginilah cara kerja teorema substitusi.
Alih-alih sumber arus jika kita memilih sumber tegangan pada langkah-3. Pada kondisi ini, nilai sumber tegangan sama dengan nilai cabang resistor 4Ω.
Pada jaringan asli, arus yang melewati cabang resistor 4Ω adalah;
Saya 1 – Saya 2 =3 – 1 =2A
Menurut hukum Ohm;
V 4Ω =2 x 4 =8V
Jadi, kita perlu menghubungkan sumber tegangan 8V dengan jaringan dan rangkaian yang tersisa seperti yang ditunjukkan pada gambar di bawah ini.
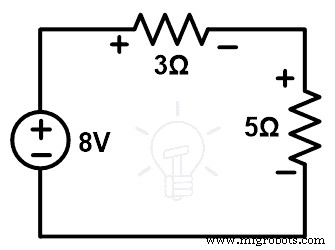
Langkah-4 Verifikasi tegangan dan arus. Terapkan KVL ke loop di atas.
8 =3Saya + 5Saya
8 =8Saya
Saya =8A
Tegangan pada resistor 3Ω;
V 3Ω =1 × 3 =3V
Tegangan pada resistor 5Ω;
V 5Ω =1 × 5 =5V
Jadi, tegangan dan arus setelah penggantian sama dengan jaringan aslinya.
Tutorial Analisis Rangkaian Listrik Terkait:
- Analisis Rangkaian SUPERNODE – Langkah demi Langkah dengan Contoh Selesai
- Analisis Rangkaian SUPERMESH – Langkah demi Langkah dengan Contoh Terpecahkan
- Hukum Arus &Tegangan Kirchhoff (KCL &KVL) | Contoh Penyelesaian
- Kalkulator Aturan Cramer – Sistem Persamaan 2 dan 3 untuk Rangkaian Listrik
- Jembatan Wheatstone – Sirkuit, Kerja, Derivasi, dan Aplikasi
- Kalkulator Teknik Elektro dan Elektronik
- 5000+ Rumus &Persamaan Teknik Elektro dan Elektronik