Aturan Pembagi Arus (CDR) – Contoh Soal untuk Sirkuit AC dan DC

Divisi Arus "CDR" untuk Rangkaian Resistif, Induktif, dan Kapasitif

Apa apakah Current Divider Rule (CDR)?

Ketika sejumlah elemen dihubungkan secara paralel, arus terbagi menjadi sejumlah jalur paralel. Dan tegangannya sama untuk semua elemen yang sama dengan tegangan sumbernya.

Dengan kata lain, ketika arus melewati lebih dari satu jalur paralel (aturan pembagi tegangan “VDR” atau pembagian tegangan digunakan untuk menghitung tegangan pada rangkaian seri), membagi arus di setiap jalur. Nilai arus yang melewati cabang tertentu bergantung pada impedansi cabang tersebut.

Aturan pembagi saat ini atau aturan pembagian saat ini adalah rumus paling penting yang banyak digunakan untuk menyelesaikan rangkaian. Kita dapat menemukan arus yang melewati setiap cabang jika kita mengetahui impedansi setiap cabang dan arus total.

Arus selalu mengalir melalui impedansi terkecil. Jadi, arus memiliki hubungan terbalik dengan impedansi. Menurut hukum ohm, arus yang masuk ke node akan dibagi antara mereka dalam proporsi terbalik dengan impedansi.

Ini berarti bahwa nilai impedansi yang lebih kecil memiliki arus yang lebih besar karena arus memilih jalur resistansi yang paling kecil. Dan resistansi nilai yang lebih besar memiliki arus paling kecil.

Menurut elemen rangkaian, aturan pembagi arus dapat menjelaskan resistor, induktor, dan kapasitor.

Aturan Pembagi Arus untuk Rangkaian Resistif

Untuk memahami aturan pembagi arus resistif, mari kita ambil rangkaian di mana resistor dihubungkan secara paralel. Diagram sirkuit ditunjukkan pada gambar di bawah ini.

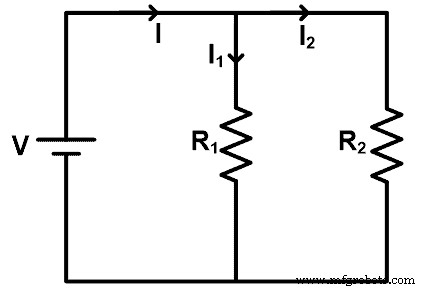
Dalam contoh ini, sumber DC mensuplai semua resistor. Tegangan resistor sama dengan tegangan sumber. Tetapi karena koneksi paralel, arus terbagi menjadi jalur yang berbeda. Arus membagi pada setiap node dan nilai arus tergantung pada resistansi.

Kita dapat langsung mencari nilai arus yang melewati setiap resistor dengan bantuan aturan pembagi arus.

Dalam contoh ini, arus utama yang disuplai oleh sumber adalah I. Dan dibagi menjadi dua resistor R₁ dan R₂ . Arus melewati resistor R₁ apakah saya₁ dan arus melewati resistor R₂ apakah saya₂ .

Karena resistor dihubungkan secara paralel. Jadi, resistansi ekivalennya adalah R_eq .

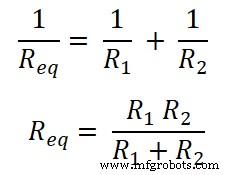
Sekarang, menurut hukum Ohm;

V =I R_eq

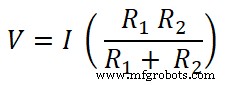
Kedua resistor dihubungkan secara paralel dengan sumber DC. Oleh karena itu, tegangan pada resistor sama dengan tegangan sumber. Dan arus yang melewati resistor R₁ apakah saya₁ .

Jadi, untuk resistor R₁;

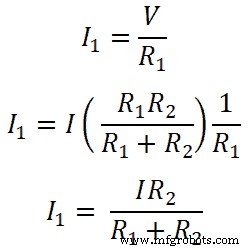
Demikian pula, untuk resister R₂;

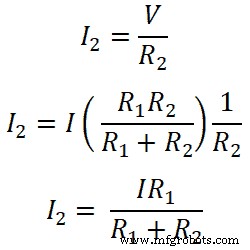
Jadi, persamaan ini menunjukkan aturan pembagi arus untuk hambatan yang dihubungkan secara paralel. Dari persamaan tersebut, kita dapat mengatakan bahwa arus yang melewati resistor sama dengan rasio perkalian antara arus total dan resistansi berlawanan dengan resistansi total.

Pos Terkait:

• Teorema Thevenin. Panduan Langkah demi Langkah dengan Contoh Terpecahkan
• Teorema Norton. Panduan Langkah demi Langkah dengan Contoh Terpecahkan

Aturan Pembagi Arus untuk Sirkuit Induktif

Bila induktor dihubungkan secara paralel, kita dapat menerapkan aturan pembagi arus untuk menemukan arus yang melewati setiap induktor. Untuk memahami aturan pembagi arus, kita ambil rangkaian di mana induktor dihubungkan secara paralel seperti yang ditunjukkan pada gambar di bawah ini.

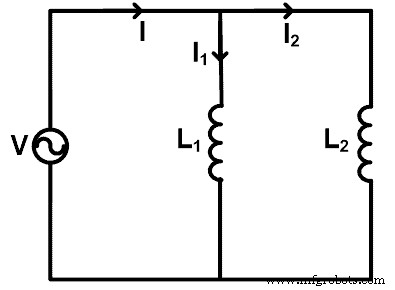
Di sini, dua induktor (L₁ dan L₂ ) dihubungkan secara paralel dengan tegangan sumber V. Arus total yang melalui sumber adalah I ampere. Arus melewati induktor L₁ apakah saya₁ dan arus melewati induktor L₂ apakah saya₂ .

Sekarang, kita perlu mencari persamaan untuk I₁ saat ini dan saya₂ . Untuk itu, kita akan menemukan induktansi ekivalen L_eq;

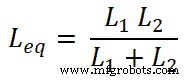
Kita tahu bahwa arus total yang melewati rangkaian adalah I dan disamakan sebagai;

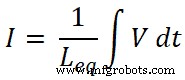
Jadi,

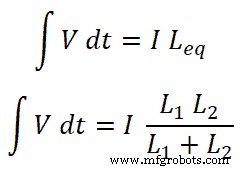
Sekarang, untuk induktor L₁ , arus yang melewati induktor ini adalah I₁;

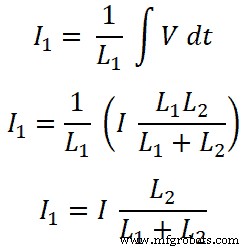
Untuk induktor L₂;

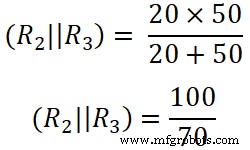
Aturan pembagi saat ini untuk induktor sama dengan aturan pembagi arus untuk resistor.

Aturan Pembagi Arus untuk Sirkuit Kapasitif

Bila kapasitor dihubungkan secara paralel, kita dapat menemukan arus yang melewati setiap kapasitor dengan menggunakan aturan pembagi arus. Untuk memahami aturan pembagi arus untuk kapasitor, kita ambil contoh di mana kapasitor dihubungkan secara paralel seperti yang ditunjukkan pada gambar di bawah ini.

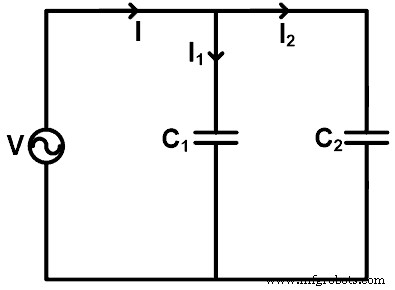
Di sini, dua kapasitor (C₁ dan C₂ ) dihubungkan secara paralel dengan sumber tegangan V. Arus melewati kapasitor C₁ adalah saya_1, dan arus melewati kapasitor C₂ apakah saya₂ . Arus total yang disuplai melalui sumber adalah I.

Sekarang, kita perlu mencari persamaan untuk I₁ saat ini dan saya₂ . Untuk itu, kita akan mencari kapasitansi ekivalen C_eq;

C_eq =C ₁ + C ₂

Kita tahu persamaan untuk arus yang melewati kapasitor. Dan persamaan untuk arus total yang disuplai oleh sumber adalah;

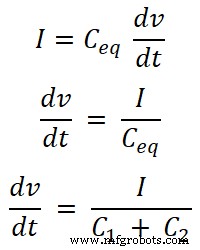
Untuk kapasitor C₁ , arus yang melewati kapasitor ini adalah I₁;

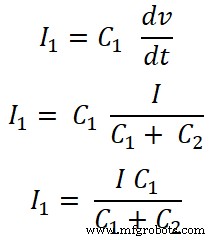
Untuk Kapasitor C₂;

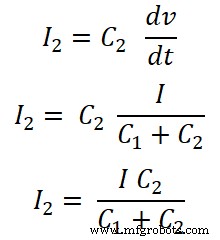
Aturan pembagi arus untuk kapasitor sedikit berbeda dari aturan pembagi arus untuk induktor dan resistor.

Dalam aturan pembagi arus kapasitor, arus yang melewati kapasitor adalah rasio dari arus total dikalikan kapasitor itu dengan kapasitansi total.

Contoh Penyelesaian untuk Rangkaian AC dan DC menggunakan CDR

Aturan Penyelam Saat Ini untuk Sirkuit DC

Contoh:1

Temukan arus yang melewati setiap resistor dengan aturan pembagi arus untuk jaringan yang diberikan.

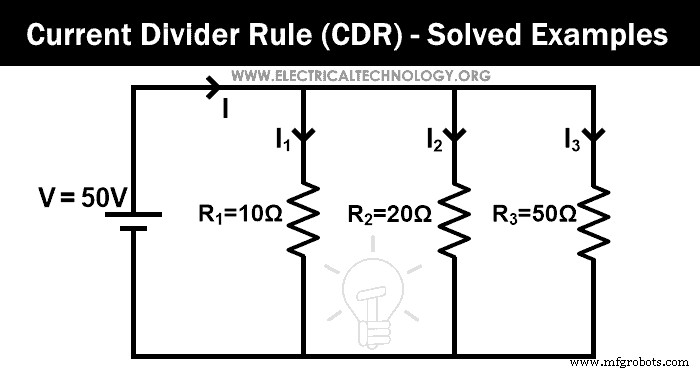
Dalam contoh ini, tiga resistor dihubungkan secara paralel. Pertama, kita cari resistansi ekivalennya.

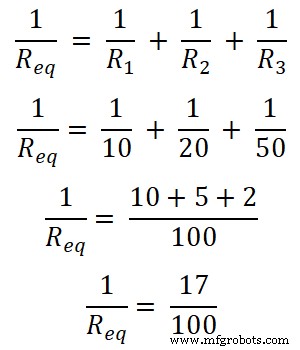
R_eq = 100/17

R_eq = 5.882

Total arus yang disuplai oleh sumber adalah I. Jadi, menurut hukum ohm;

V =I R_eq

50V =Saya (5.882Ω)

I = 50V / 5.882Ω

I = 8.5 A

Sekarang, kita menerapkan aturan pembagi arus ke resistor pertama (10 ), dan arus yang melewati resistor ini adalah I₁;

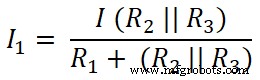
Di sini R₂ dan R₃ dihubungkan secara paralel. Jadi, kita perlu mencari resistansi ekivalen antara R₂ dan R₃ .

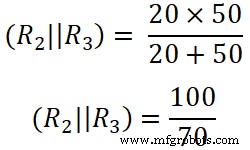
(R ₂ || R ₃ ) =14,285

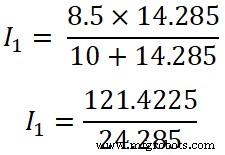
Saya ₁ =4.9999 5 A

Demikian pula, kami menerapkan aturan pembagi arus ke resistor Kedua (20 ), dan arus yang melewati resistor ini adalah I₂;

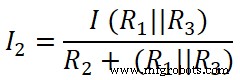
Di sini,

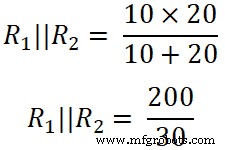
(R ₁ || R ₃ ) =8,33

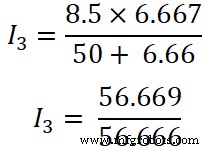
Saya ₂ =2,499 2,5 A

Sekarang, kita menerapkan aturan pembagi arus ke resistor ketiga (50 ), dan arus yang melewati resistor ini adalah I₃ .

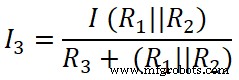
Di sini,

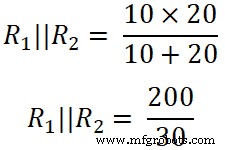
(R ₁ || R ₂ ) =6,66

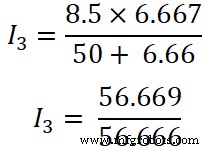
Saya ₃ =1,00 A

Jadi, penjumlahan ketiga arus adalah;

Saya ₁ + Saya ₂ + Saya ₃ =5 + 2,5 + 1 =8,5 A

Dan arus ini sama dengan arus total yang disuplai oleh sumber.

Aturan Penyelam Saat Ini untuk Sirkuit AC

Contoh-2

Pertimbangkan rangkaian AC yang memiliki resistor dan kapasitor yang dihubungkan secara paralel seperti yang ditunjukkan pada gambar di bawah. Temukan arus yang melewati resistor dan kapasitor menggunakan aturan pembagi arus. Pertimbangkan frekuensi 60 Hz.

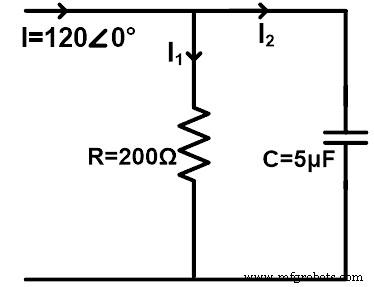
Z_R =200 =200∠0°Ω

Z_C =1/(2 f C) =1/(2 60(5×10 ⁶ ) )

Z_C =10 ⁶ / (600 )

Z_C =530,78 -90°

Sekarang, menurut aturan pembagi arus, persamaan arus yang melewati resistor adalah;

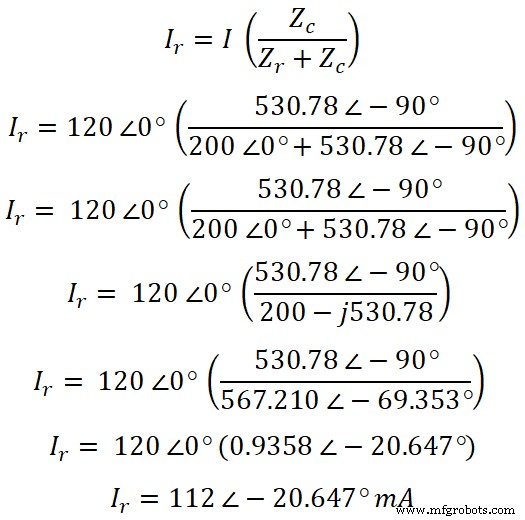
Sekarang, dengan cara yang sama, kita dapat menemukan arus yang melewati kapasitor. Menurut aturan pembagi arus, persamaan arus yang melalui kapasitor adalah;

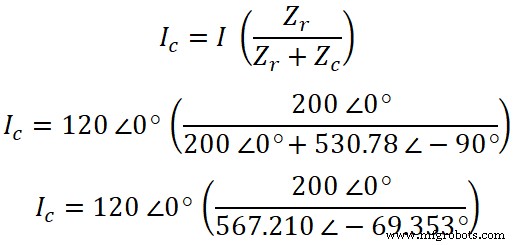
Saya_C =120 0° (0,3526 69,353°)

Saya_C =42,31 69,353°

Jika Anda ingin membuktikan jawaban ini, Anda dapat menambahkan kedua arus. Dan nilai arus ini sama dengan arus sumber.

Tutorial Analisis Rangkaian Listrik Terkait:

• Teorema Kompensasi – Bukti, Penjelasan, dan Contoh Penyelesaian
• Teorema Substitusi – Panduan Langkah demi Langkah dengan Contoh Selesai
• Analisis Rangkaian SUPERNODE – Langkah demi Langkah dengan Contoh Selesai
• Analisis Rangkaian SUPERMESH – Langkah demi Langkah dengan Contoh Selesai
• Hukum Arus &Tegangan Kirchhoff (KCL &KVL) | Contoh Penyelesaian
• Kalkulator Aturan Cramer – Sistem Persamaan 2 dan 3 untuk Rangkaian Listrik
• Jembatan Wheatstone – Sirkuit, Kerja, Derivasi, dan Aplikasi
• Kalkulator Teknik Elektro dan Elektronik
• 5000+ Rumus &Persamaan Teknik Elektro dan Elektronik