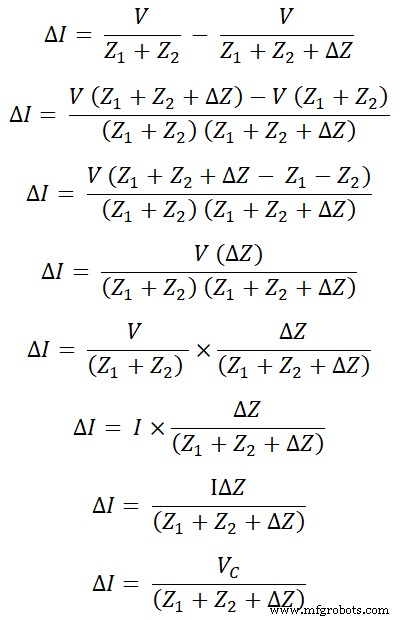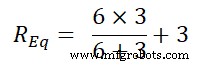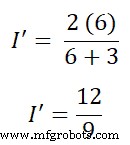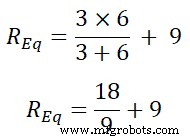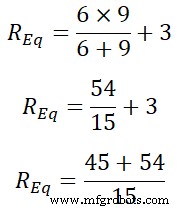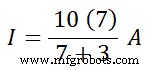Bersamaan dengan teori jaringan, penting untuk mengetahui atau mempelajari pengaruh perubahan impedansi di salah satu cabangnya. Ini akan mempengaruhi tegangan dan arus yang sesuai dari jaringan atau sirkuit. Teorema kompensasi memberikan informasi tentang perubahan dalam jaringan.
Teorema kompensasi bekerja berdasarkan konsep dasar hukum Ohm. Menurut hukum Ohm, ketika arus melewati resistor, sejumlah penurunan tegangan terjadi pada resistor. Penurunan tegangan ini akan melawan tegangan sumber.
Oleh karena itu, kami menghubungkan sumber tegangan ekstra dalam polaritas yang berlawanan dibandingkan dengan tegangan sumber dan besarnya sama dengan penurunan tegangan. Teorema kompensasi bekerja pada konsep ini.
Teorema kompensasi menyatakan bahwa,
Untuk memahami teorema kompensasi, perhatikan gambar di bawah ini.
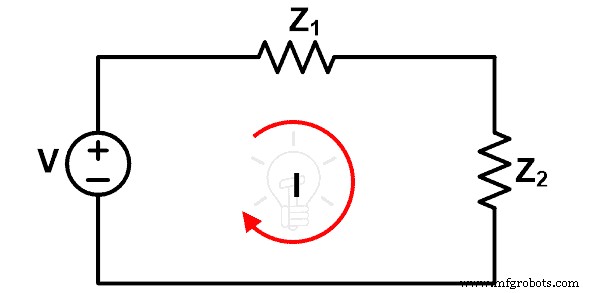
Pada gambar ini, sumber tegangan V adalah tegangan dan sumber independen dan dua impedansi Z1 dan Z2 adalah elemen linier atau bilateral. Oleh karena itu, kita dapat menerapkan teorema kompensasi ke jaringan ini. Arus yang melewati loop adalah I.
Sekarang, asumsikan bahwa impedansi Z2 meningkat sebesar Z. Karena perubahan ini, arus yang melewati loop berubah dan itu adalah I'. Diagram sirkuit baru ditunjukkan pada gambar di bawah ini.
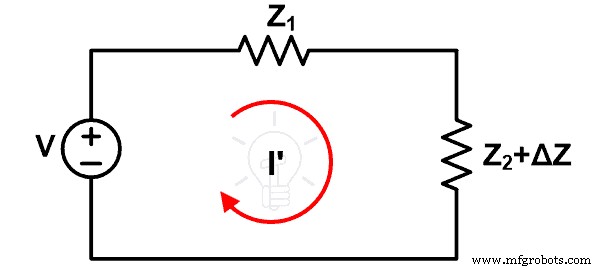
Karena perubahan impedansi, perubahan arus diberikan oleh I.
ΔSaya =Saya – Saya
Menurut pernyataan teorema kompensasi, kita dapat langsung menghitung perubahan I saat ini. Untuk itu, kita perlu memodifikasi sirkuitnya.
Modifikasi pertama adalah, sambungkan sumber tegangan bernilai I∆Z di cabang yang impedansinya diubah. Dan polaritas sumber tegangan ini berlawanan dengan sumber utama. Sumber tegangan yang baru ditambahkan VC dikenal sebagai sumber kompensasi.
VC =Saya Z
Modifikasi kedua adalah kita perlu menghapus sumber tegangan lama dengan impedansi internalnya. Jika kita mempertimbangkan sumber tegangan yang ideal, dalam kondisi ini, kita dapat menghilangkan sumber tegangan ini dengan melakukan hubungan pendek pada terminalnya. Setelah modifikasi ini, rangkaian yang tersisa adalah seperti yang ditunjukkan pada gambar di bawah ini.
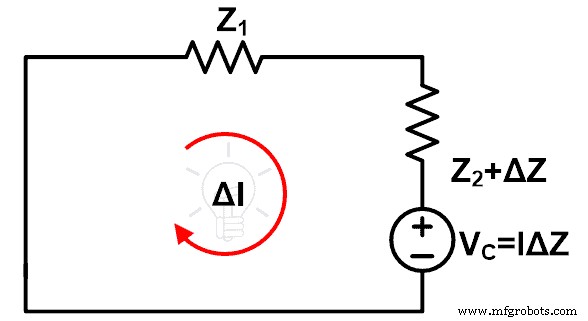
Dengan menyelesaikan rangkaian di atas, kita dapat dengan mudah menemukan perubahan arus setelah perubahan impedansi.
Perhatikan rangkaian yang diberikan pada gambar-1. Hitung arus (I) yang melewati loop.
Terapkan KVL ke gambar-1;
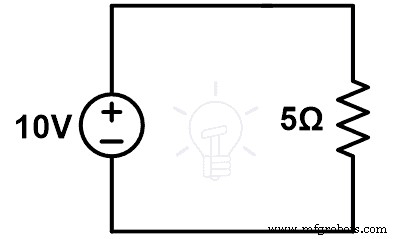
Sekarang, kita telah mengasumsikan bahwa impedansi Z2 diubah oleh Z. Dan rangkaian yang dimodifikasi adalah seperti yang ditunjukkan pada gambar-2. Kita perlu menghitung (I’) arus yang melewati loop pada gambar-2.
Terapkan KVL ke gambar-2;
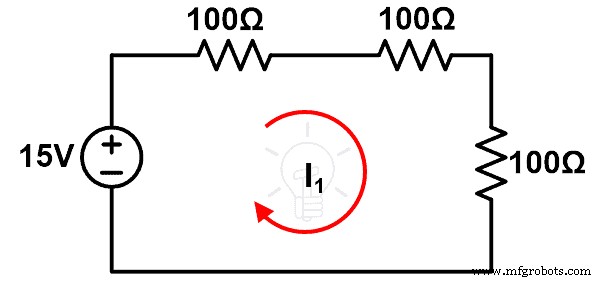
Karena perubahan impedansi, perubahan arus loop dilambangkan sebagai I. Dan I sama dengan selisih antara I arus lama dan I arus baru’.
ΔSaya =Saya – Saya
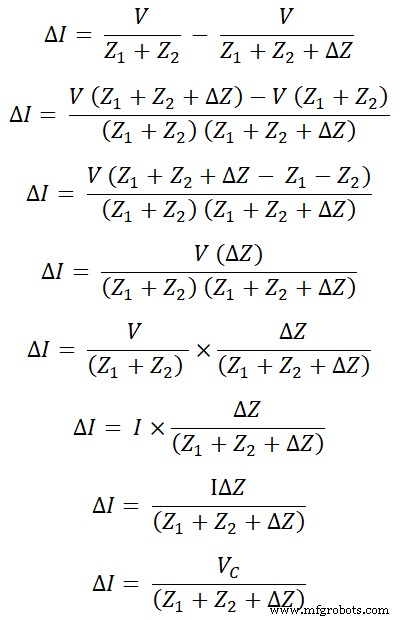
Sekarang, perhatikan gambar di bawah ini.
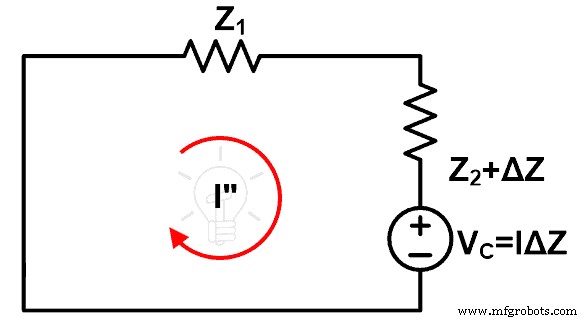
Angka ini mewakili rangkaian setelah penerapan teorema kompensasi. Di sini, sumber tegangan asli dihilangkan dengan hubungan arus pendek (anggap sumber tegangan ideal).
Kita akan menemukan arus yang melewati loop ini yaitu I”. Dan bandingkan arus ini dengan arus yang dihitung di atas.
Untuk menghitung arus yang melewati loop, terapkan KVL pada gambar di atas.
VC =Z 1 Saya” +(Z 2 +ΔZ ) Saya”
VC =Saya” (Z 1 + Z 2 + Z )
Saya” =VC / (Z 1 + Z 2 + Z )
Saya” =Saya
Dengan demikian, terbukti bahwa perubahan arus (∆I) setelah modifikasi adalah sama dengan arus yang dihitung dengan teorema kompensasi.
Dan kami telah membuktikan pernyataan teorema kompensasi.
Tujuan: Buktikan teorema kompensasi dan temukan perubahan arus.
Aparat: Voltmeter, Ammeter, Resistor, Kabel penghubung, Breadboard,
Diagram sirkuit:
Prosedur:
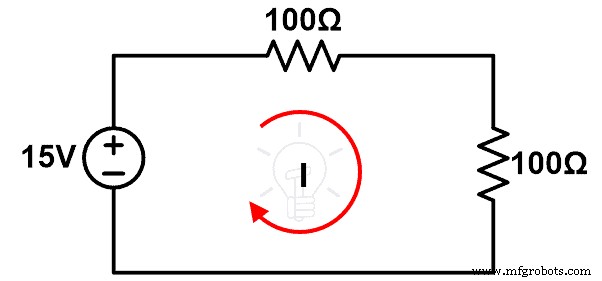
Langkah-1 Hubungkan komponen seperti yang ditunjukkan pada gambar-5 menggunakan kabel penghubung pada papan tempat memotong roti.
Langkah-2 Ukur I saat ini.
Langkah-3 Hubungkan komponen seperti yang ditunjukkan pada gambar-6. Di sini, kami telah menghubungkan resistor tambahan.
Langkah-4 Ukur I1 saat ini.
Langkah-5 Hitung perubahan arus (∆I) dari nilai I dan I1.
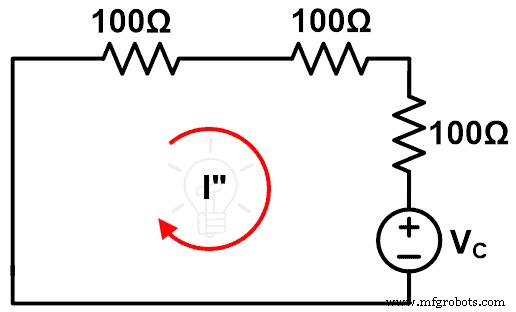
Langkah-6 Hubungkan komponen seperti yang ditunjukkan pada gambar-7. Sirkuit ini adalah sirkuit kompensasi.
Langkah-7 Ukur I saat ini”.
Langkah-8 Bandingkan perubahan arus (∆I) dengan I”.
Tabel Eksperimen:
| Sr. Tidak. | Saya | Saya 1 | ∆Saya | Saya” |
| 1 |
Hasil:
Dengan membandingkan nilai arus I’’ dengan I, kita dapat membuktikan teorema kompensasi.
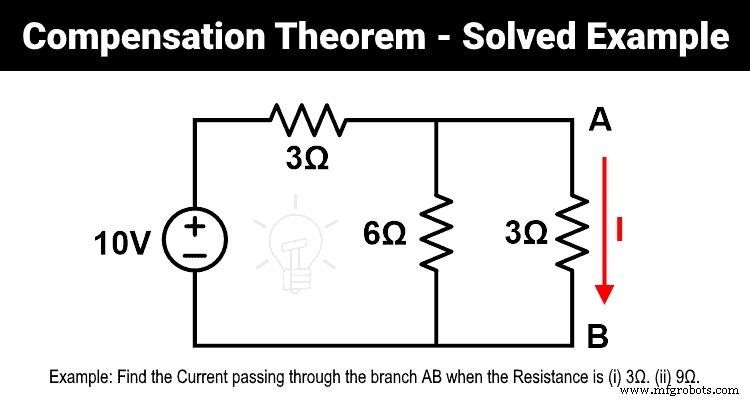
Answer-1
Seperti yang ditunjukkan pada gambar, resistor 6Ω dan 3Ω berada secara paralel. Dan kombinasi paralel ini dihubungkan secara seri dengan resistor 3Ω. Oleh karena itu, resistansi ekivalennya adalah;
R Persamaan =6 | | 3+3
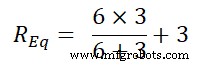
R Persamaan =2 + 3
R Persamaan =5
Menurut hukum Ohm;
10 =Saya (5)
Saya =10 5
Saya =2 J
Sekarang, kita perlu mencari arus yang melewati cabang AB. Jadi, menurut aturan pembagi saat ini;
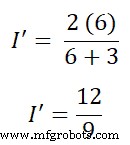
Saya =1,333 A (atau 3/4 A)
Answer-2
Kita perlu mengganti resistor 3Ω dengan resistor 9Ω. Menurut teorema kompensasi, kita perlu menambahkan sumber tegangan baru secara seri dengan resistor 9Ω. Dan nilai dari sumber tegangan ini adalah;
VC =Saya Z
Di mana,
Z =9 – 3 =6 dan Saya =4/3 A (atau 1,333 A)
VC =(4/3A) x 6
VC =8 V
Diagram sirkuit yang dimodifikasi atau diagram sirkuit terkompensasi adalah seperti yang ditunjukkan pada gambar di bawah ini.
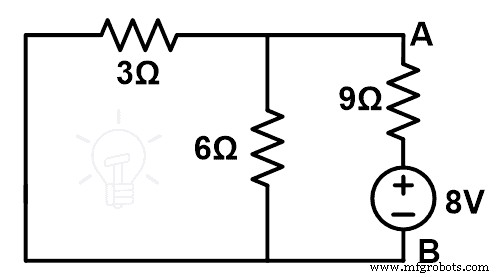
Sekarang, kita akan menemukan resistansi yang setara. Di sini, resistor 3Ω dan 6Ω dihubungkan secara paralel. Dan kombinasi paralel ini dihubungkan secara seri dengan resistor 9Ω.
RPersamaan =3 | | 6 + 9
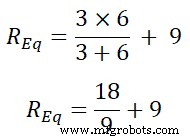
RPersamaan =2 + 9
RPersamaan =11
Sekarang, menurut hukum Ohm;
V =I R
8 =Saya (11 )
ΔSaya =8 11
ΔSaya =0,7272 A
Jadi, menurut teorema kompensasi; perubahan arus adalah 0,7272A.
Answer-3
Kami ingin membuktikan teorema kompensasi. Jadi, kami menghitung arus dalam contoh yang diberikan dengan resistor 9Ω.
Diagram rangkaian yang dimodifikasi ditunjukkan pada gambar di bawah.
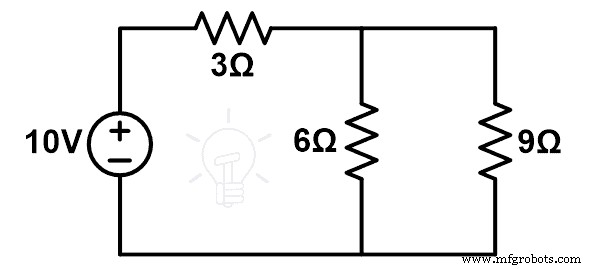
Di sini, resistor 9Ω dan 6Ω dihubungkan secara paralel dan kombinasi paralel ini dihubungkan secara seri dengan resistor 3Ω.
Resistensi yang setara sama dengan;
RPersamaan =9 | | 6 + 3
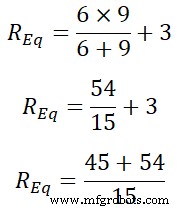
RPersamaan =99 15
RPersamaan =6,66
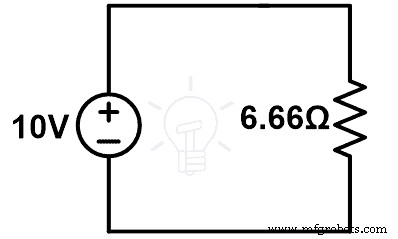
Dari gambar di atas;
10 =Saya (6.66)
Saya =10 6,66
Saya =1,5151 A
Menurut aturan pembagi saat ini;
Saya” =0.6060A
ΔSaya =Saya – Saya”
ΔSaya =(4/3A) – 0,6060
ΔSaya =1,333A – 0,6060
ΔSaya =0,7273 A
Dengan demikian, terbukti bahwa perubahan arus yang dihitung dari teorema kompensasi sama dengan perubahan arus yang dihitung dari rangkaian aslinya.
Pada rangkaian di bawah, tentukan perubahan arus jika resistor 3Ω diganti dengan resistor 7Ω menggunakan teorema kompensasi. Dan buktikan teorema kompensasi.
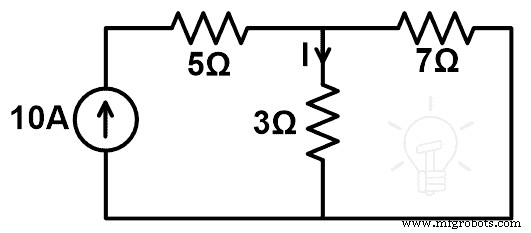
Jaringan di atas hanya terdiri dari resistor dan sumber arus independen. Jadi, kita dapat menerapkan teorema kompensasi ke jaringan ini.
Pada gambar ini, jaringan dipasok oleh sumber saat ini. Sekarang, kita perlu mencari arus yang melewati cabang resistor 3Ω. Arus ini dapat ditemukan menggunakan KCL atau KVL. Tapi di sini, arus ini dapat dengan mudah ditemukan dengan aturan pembagi saat ini.
Oleh karena itu, sesuai dengan aturan pembagi saat ini;
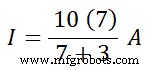
Saya =70 10 A
Saya =7 A
Pada jaringan asli dengan resistor 3Ω, arus yang melewati cabang tersebut adalah 3A. Sekarang, kita perlu mengubah resistor ini dari 3Ω menjadi 7Ω. Karena modifikasi ini, arus yang melewati cabang itu akan diubah. Dan kita akan menemukan perubahan arus ini dengan teorema kompensasi.
Untuk itu, kita perlu membuat jaringan kompensasi. Untuk membuat jaringan kompensasi, kita perlu menghapus semua sumber independen yang tersedia di jaringan dengan melakukan hubungan arus pendek sumber tegangan dan hubungan arus terbuka sumber arus.
Dalam jaringan ini, hanya satu sumber saat ini yang tersedia. Kami menganggap sumber arus adalah sumber arus yang ideal. Oleh karena itu, kita tidak perlu menambahkan resistansi internal.
Modifikasi kedua yang perlu kita lakukan pada rangkaian kompensasi adalah dengan menambahkan sumber tegangan tambahan. Dan nilai tegangan ini adalah;
VC =Saya Z
VC =7 × (7 – 3)
VC =7 × 4
VC =28 V
Jaringan kompensasi seperti yang ditunjukkan pada gambar di bawah.
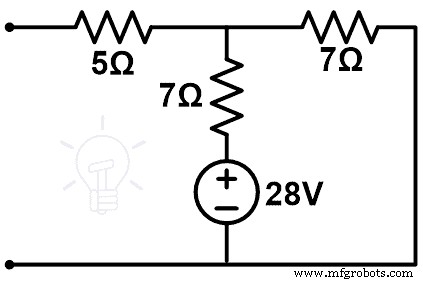
Angka ini hanya memiliki satu loop. Dan arus yang melewati cabang 7Ω akan memberikan perubahan arus (∆I).
ΔSaya =VC (7+7)
ΔSaya =28 14
ΔSaya =2 J
Untuk membuktikan teorema kompensasi, kita akan mencari arus pada rangkaian dengan resistor 7Ω yang terhubung. Diagram sirkuit yang dimodifikasi ditunjukkan pada gambar di bawah ini.
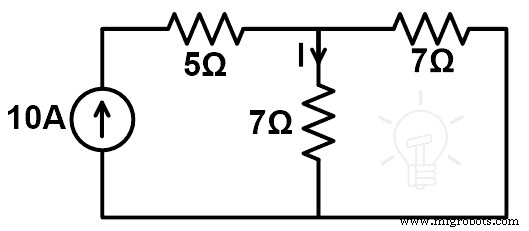
Saya” =(10 (7)) (7 + 7)
Saya” =70 14
Saya” =5 A
Dengan menerapkan aturan pembagi saat ini;
Untuk menemukan perubahan arus, kita perlu mengurangi arus ini dari arus yang melewati jaringan asli.
ΔSaya =Saya – Saya”
ΔSaya =7 – 5
ΔSaya =2 J
Oleh karena itu, kami telah membuktikan teorema kompensasi.
Tutorial Analisis Rangkaian Listrik Terkait:
Teknologi Industri
Divisi Tegangan “VDR” untuk Rangkaian Resistif, Induktif, dan Kapasitif Apa itu Aturan Pembagi Tegangan? Dalam sebuah rangkaian, ketika sejumlah elemen dihubungkan secara seri, tegangan input terbagi di seluruh elemen. Dan dalam sebuah rangkaian, ketika sejumlah elemen dihubungkan secara paralel, a
Divisi Arus CDR untuk Rangkaian Resistif, Induktif, dan Kapasitif Apa apakah Current Divider Rule (CDR)? Ketika sejumlah elemen dihubungkan secara paralel, arus terbagi menjadi sejumlah jalur paralel. Dan tegangannya sama untuk semua elemen yang sama dengan tegangan sumbernya. Dengan kata lain, ke
Menganalisis &Menyelesaikan Rangkaian Listrik Menggunakan Teorema Substitusi Teorema Substitusi Seperti namanya, teorema substitusi digunakan untuk mengganti satu elemen rangkaian dengan elemen lain. Namun saat mengganti elemen, Anda harus ingat bahwa perilaku rangkaian tidak boleh berubah. Teorema
Software ERP Manufacturing juga dikenal sebagai MRP, adalah ERP khusus untuk manufaktur. Saat memilih sistem ERP baru, perusahaan perlu membuat beberapa perbandingan dan analisis. Itu karena solusi ERP merupakan investasi jangka panjang bagi perusahaan. Oleh karena itu, proses seleksi perlu banyak m
