Peta Karnaugh yang lebih besar mengurangi desain logika yang lebih besar. Seberapa besar cukup besar? Itu tergantung pada jumlah input, penggemar , ke rangkaian logika yang dipertimbangkan. Salah satu perusahaan logika besar yang dapat diprogram memiliki jawabannya.
Data Altera sendiri, yang diambil dari perpustakaan desain pelanggannya, mendukung nilai heterogenitas. Dengan memeriksa kerucut logika, memetakannya ke node berbasis LUT dan menyortirnya berdasarkan jumlah input yang terbaik di setiap node, Altera menemukan bahwa distribusi fan-in hampir rata antara dua dan enam input, dengan puncak yang bagus pukul lima.
Jawabannya adalah tidak lebih dari enam input untuk hampir semua desain, dan lima input untuk desain logika rata-rata. Lima variabel peta Karnaugh berikut.
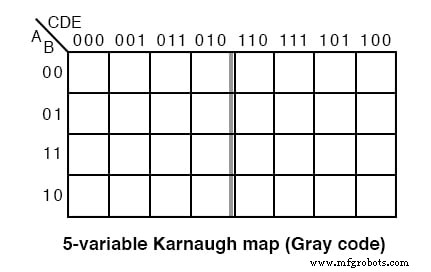
Versi lama dari lima variabel K-map, peta Kode Abu-abu atau peta refleksi, ditampilkan di atas. Bagian atas (dan samping untuk peta 6-variabel) peta diberi nomor dengan kode abu-abu penuh. Kode Gray mencerminkan sekitar tengah kode. Peta gaya ini ditemukan dalam teks-teks lama. Gaya pilihan yang lebih baru ada di bawah.
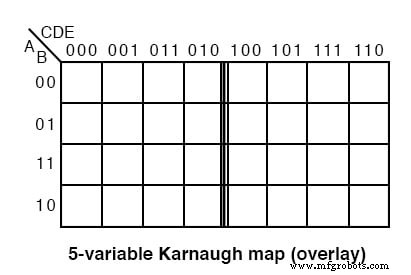
Versi overlay peta Karnaugh, yang ditunjukkan di atas, hanyalah dua (empat untuk peta 6-variabel) yang identik kecuali untuk bit paling signifikan dari alamat 3-bit di bagian atas.
Jika kita melihat pada bagian atas peta, kita akan melihat bahwa penomoran berbeda dengan peta kode Gray sebelumnya. Jika kita mengabaikan digit terpenting dari 3 angka tersebut, barisan 00, 01, 11, 10 berada pada heading kedua sub peta dari peta overlay. Urutan delapan angka 3 digit bukan kode Gray. Padahal urutan empat dari dua bit terkecil adalah.
Mari kita gunakan Peta Karnaugh 5-variabel. Rancang rangkaian yang memiliki input biner 5-bit (A, B, C, D, E), dengan A sebagai MSB (Bit Paling Signifikan). Ini harus menghasilkan logika keluaran Tinggi untuk setiap bilangan prima yang terdeteksi dalam data masukan.
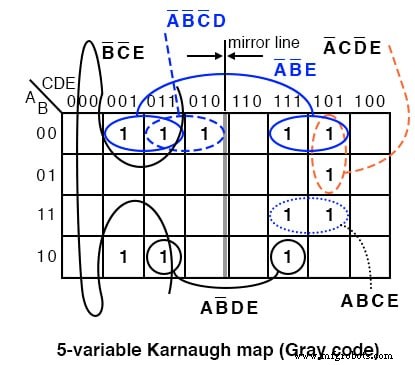
Kami menunjukkan solusi di atas pada peta kode Abu-abu (refleksi) yang lebih tua untuk referensi. Bilangan prima adalah (1,2,3,5,7,11,13,17,19,23,29,31). Plot a 1 di setiap sel yang sesuai. Kemudian, lanjutkan dengan pengelompokan sel. Akhiri dengan menulis hasil yang disederhanakan.
Perhatikan bahwa kelompok 4-sel A'B'E terdiri dari dua pasang sel di kedua sisi garis cermin. Hal yang sama berlaku untuk grup 2 sel AB'DE. Ini adalah sekelompok 2-sel dengan dipantulkan tentang garis cermin. Saat menggunakan versi K-map ini, cari gambar cermin di bagian lain peta.
Keluar =A'B'E + B'C'E + A'C'DE + A'CD'E + ABCE + AB'DE + A'B'C'D
Di bawah ini kami menampilkan versi yang lebih umum dari peta 5-variabel, peta overlay.
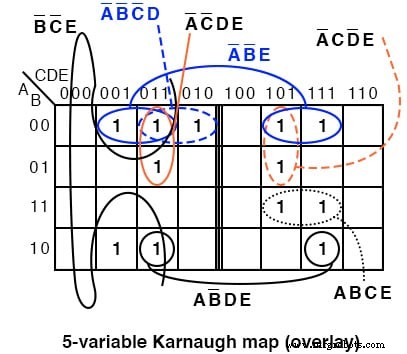
Jika kita membandingkan pola di kedua peta, beberapa sel di bagian kanan peta akan dipindahkan karena pengalamatan di bagian atas peta berbeda. Kita juga perlu mengambil pendekatan berbeda dalam menemukan kesamaan antara dua bagian peta.
Overlay satu setengah dari peta di atas setengah lainnya. Setiap tumpang tindih dari peta atas ke peta bawah adalah grup potensial. Gambar di bawah menunjukkan bahwa grup AB'DE terdiri dari dua sel yang ditumpuk. Grup A'B'E terdiri dari dua pasang sel yang ditumpuk.
Untuk A'B'E grup 4-sel ABCDE =00xx1 untuk grup. Artinya A,B,E sama 001 masing-masing untuk kelompok. Dan, CD=xx itu bervariasi, tidak ada kesamaan di CD=xx untuk kelompok 4-sel. Karena ABCDE =00xx1 , kelompok 4-sel dicakup oleh A'B'XXE =A'B'E .
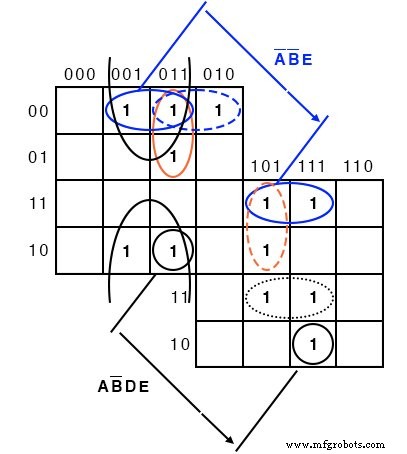
Peta overlay 5-variabel di atas ditampilkan bertumpuk.
Contoh peta Karnaugh enam variabel berikut. Kami telah menumpuk empat sub peta secara mental untuk melihat grup 4-sel yang sesuai dengan Out =C'F'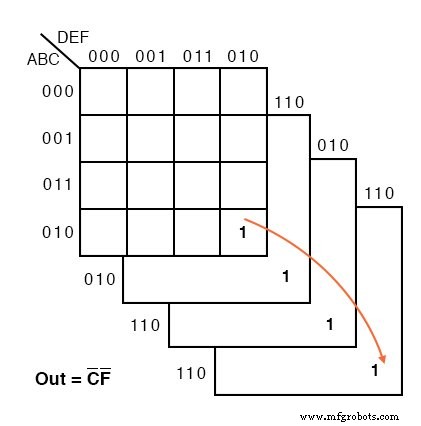 
Pembanding magnitudo (digunakan untuk mengilustrasikan peta-K 6-variabel) membandingkan dua bilangan biner, yang menunjukkan apakah keduanya sama, lebih besar, atau lebih kecil satu sama lain pada tiga keluaran masing-masing. Pembanding magnitudo tiga bit memiliki dua input A2 A1 A0 dan B2 B1 B0 Pembanding magnitudo sirkuit terpadu (7485) sebenarnya akan memiliki empat input, Tapi, peta Karnaugh di bawah ini perlu dijaga agar ukurannya masuk akal. Kami hanya akan menyelesaikan A>B keluaran.
Di bawah, peta Karnaugh 6-variabel membantu penyederhanaan logika untuk komparator magnitudo 3-bit. Ini adalah jenis peta overlay. Kode alamat biner di bagian atas dan bawah sisi kiri peta bukan kode Gray 3-bit penuh.
Padahal kode alamat 2 bit dari keempat sub peta tersebut adalah kode Gray. Temukan ekspresi yang berlebihan dengan menumpuk empat sub peta di atas satu sama lain (ditunjukkan di atas). Mungkin ada sel yang sama untuk keempat peta, meskipun tidak dalam contoh di bawah ini. Itu memang memiliki sel yang sama dengan pasangan sub peta.
Output A>B di atas adalah ABC>XYZ pada peta di bawah.
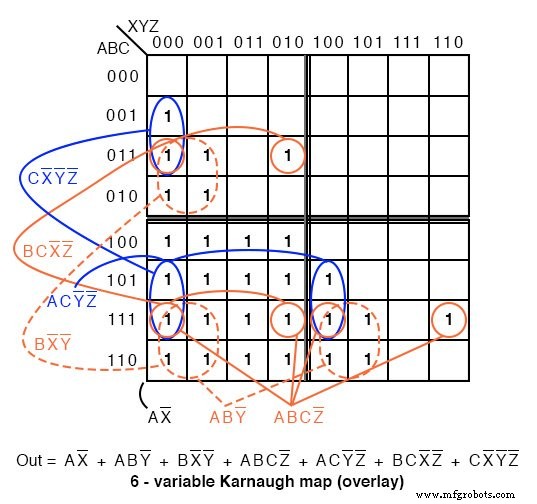
Di mana pun ABC lebih besar dari XYZ , a 1 diplot. Di baris pertama ABC=000 tidak boleh lebih besar dari salah satu nilai XYZ . Tidak ada 1 s di baris ini. Di baris kedua, ABC=001 , hanya sel pertama ABCXYZ=001000 adalah ABC lebih besar dari XYZ . Satu 1 dimasukkan dalam sel pertama dari baris kedua. Baris keempat, ABC=010 , memiliki sepasang 1 S. Baris ketiga, ABC=011 memiliki tiga 1 S. Dengan demikian, peta diisi dengan 1 s di sel mana pun di mana ABC lebih besar dari XXZ .
Dalam mengelompokkan sel, bentuk grup dengan sub peta yang berdekatan jika memungkinkan. Semua kecuali satu kelompok 16-sel melibatkan sel-sel dari pasangan sub peta. Cari grup berikut:
Kelompok 16-sel, AX' menempati semua sub peta kanan bawah; meskipun, kami tidak melingkarinya pada gambar di atas.
Satu grup 8-sel terdiri dari sekelompok 4-sel di sub peta atas yang melapisi grup serupa di peta kiri bawah. Kelompok 8 sel kedua terdiri dari kelompok 4 sel serupa di sub peta kanan yang melapisi kelompok 4 sel yang sama di peta kiri bawah.
Empat kelompok 4-sel ditampilkan pada peta Karnaugh di atas dengan istilah produk terkait. Bersama dengan istilah produk untuk dua kelompok sel 8 dan kelompok 16 sel, pengurangan Jumlah Produk akhir ditampilkan, semua tujuh istilah.
Menghitung 1 s di peta, ada total 16+6+6=28 yang. Sebelum pengurangan logika K-map akan ada 28 istilah produk dalam output SOP kami, masing-masing dengan 6 input. Peta Karnaugh menghasilkan tujuh suku produk dari empat input atau kurang. Ini benar-benar tentang peta Karnaugh!
Diagram pengkabelan tidak ditampilkan. Namun, berikut adalah daftar bagian untuk komparator magnitudo 3-bit untuk ABC>XYZ menggunakan 4 bagian keluarga logika TTL:
TINJAUAN:
Teknologi Industri
Apa itu Hashmap di Java? HashMap pada dasarnya menunjuk kunci unik ke nilai corresponding yang sesuai yang dapat diambil pada titik tertentu. Fitur Java Hashmap a) Nilai dapat disimpan dalam peta dengan membentuk nilai kunci pasangan. Nilai dapat diambil menggunakan kunci dengan meneruskannya k
Dibutuhkan lebih dari sekadar situs web yang mencolok dan email promosi yang cerdas untuk bersaing di arena pemasaran manufaktur. Kemungkinannya adalah, pesaing Anda yang lebih besar menawarkan produk dan layanan serupa ke basis klien yang sama. Solusi industri perusahaan Anda mungkin menawarkan fit
Peta situs interaktif dan denah lantai adalah cara yang bagus untuk menempatkan teknisi pemeliharaan Anda tepat di tempat yang Anda butuhkan, dengan cepat. Tim Anda berhenti berlari berputar-putar, dan mulai bergerak dalam garis lurus. Tetapi dengan perangkat lunak CMMS yang tepat, Anda dapat meng
Printer 3D FDM saat ini tersedia di pasaran dalam berbagai volume build. Dari printer dengan alas 15 x 15 cm hingga alas 50 x 50 cm. Ada kepercayaan umum bahwa semakin besar volume build, semakin baik. Ini karena alasan bahwa semua yang dapat dicetak pada printer kecil dapat dicetak pada printer bes
