Metode Saat Ini Cabang

Teknik analisis jaringan pertama dan paling mudah disebut Metode Saat Ini Cabang . Dalam metode ini, kita mengasumsikan arah arus dalam jaringan, kemudian menulis persamaan yang menggambarkan hubungan mereka satu sama lain melalui Hukum Kirchhoff dan Ohm. Setelah kita memiliki satu persamaan untuk setiap arus yang tidak diketahui, kita dapat menyelesaikan persamaan simultan dan menentukan semua arus, dan oleh karena itu semua tegangan turun di jaringan.

Penyelesaian Menggunakan Metode Cabang Saat Ini

Mari gunakan rangkaian ini untuk mengilustrasikan metodenya:

Memilih Node

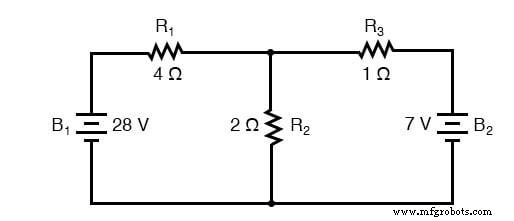
Langkah pertama adalah memilih simpul (persimpangan kabel) di sirkuit untuk digunakan sebagai titik referensi untuk arus kita yang tidak diketahui. Saya akan memilih simpul yang bergabung di sebelah kanan R₁ , bagian atas R₂ , dan kiri R₃ .

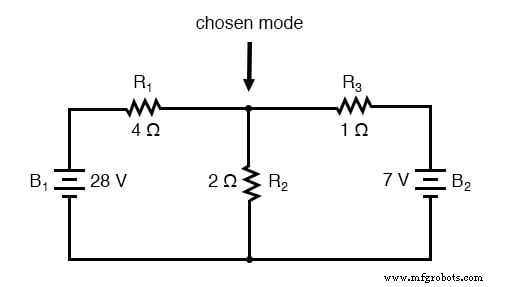
Pada simpul ini, tebak arah mana yang diambil arus ketiga kabel, beri label pada ketiga arus tersebut sebagai I₁ , saya₂ , dan saya₃ , masing-masing. Ingatlah bahwa arah arus ini bersifat spekulatif pada titik ini. Untungnya, jika ternyata salah satu tebakan kita salah, kita akan tahu kapan kita memecahkan arus secara matematis (arah arus yang "salah" akan muncul sebagai angka negatif dalam solusi kita).

Terapkan Hukum Arus Kirchhoff (KCL)

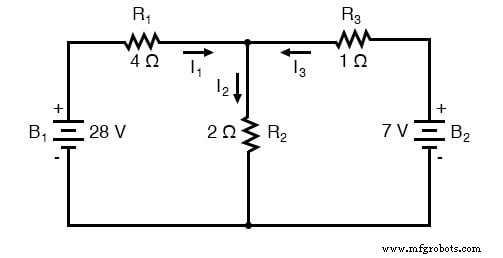
Hukum Arus Kirchhoff (KCL) memberi tahu kita bahwa jumlah aljabar arus yang masuk dan keluar suatu simpul harus sama dengan nol, sehingga kita dapat menghubungkan ketiga arus ini (I₁ , saya₂ , dan saya₃ ) satu sama lain dalam satu persamaan. Demi konvensi, saya akan menunjukkan setiap masuk saat ini simpul sebagai tanda positif, dan arus keluar simpul sebagai tanda negatif:

Label Semua Penurunan Tegangan

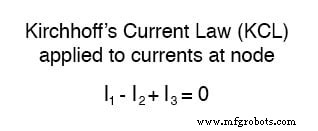
Langkah selanjutnya adalah memberi label semua polaritas penurunan tegangan pada resistor sesuai dengan arah arus yang diasumsikan. Polaritas positif di mana arus masuk ke resistor dan negatif di mana ia keluar dari resistor:

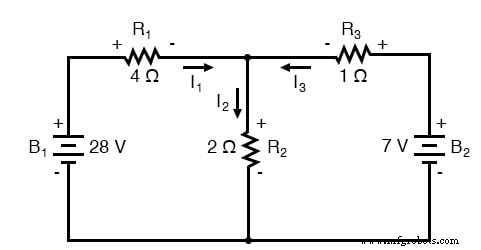
Polaritas baterai, tentu saja, tetap sesuai dengan simbologinya (negatif ujung pendek, ujung panjang positif). Tidak apa-apa jika polaritas penurunan tegangan resistor tidak sesuai dengan polaritas baterai terdekat, asalkan polaritas tegangan resistor benar berdasarkan asumsi arah arus yang melaluinya. Dalam beberapa kasus, kami mungkin menemukan bahwa arus akan dipaksa kembali melalui baterai, menyebabkan efek ini. Hal penting untuk diingat di sini adalah mendasarkan semua polaritas resistor Anda dan perhitungan selanjutnya pada arah arus yang awalnya diasumsikan. Seperti yang dinyatakan sebelumnya, jika asumsi Anda salah, itu akan terlihat setelah persamaan diselesaikan (melalui solusi negatif). Namun, besarnya solusi akan tetap benar.

Terapkan Hukum Tegangan Kirchhoff (KVL)

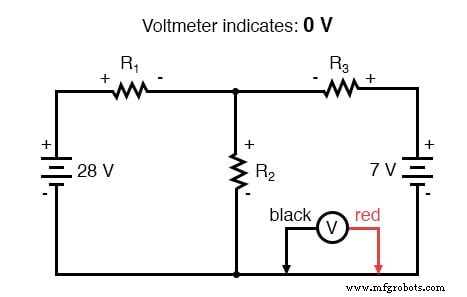
Hukum Tegangan Kirchhoff (KVL) memberitahu kita bahwa jumlah aljabar dari semua tegangan dalam satu lingkaran harus sama dengan nol, sehingga kita dapat membuat lebih banyak persamaan dengan istilah saat ini (I₁ , saya₂ , dan saya₃ ) untuk persamaan simultan kami. Untuk mendapatkan persamaan KVL, kita harus menghitung penurunan tegangan dalam satu lingkaran rangkaian, seolah-olah kita sedang mengukur dengan voltmeter nyata. Saya akan memilih untuk melacak loop kiri sirkuit ini terlebih dahulu, mulai dari sudut kiri atas dan bergerak berlawanan arah jarum jam (pilihan titik awal dan arahnya sewenang-wenang). Hasilnya akan terlihat seperti ini:

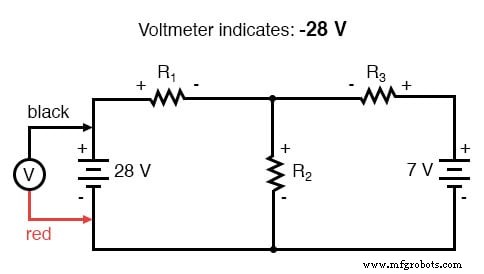
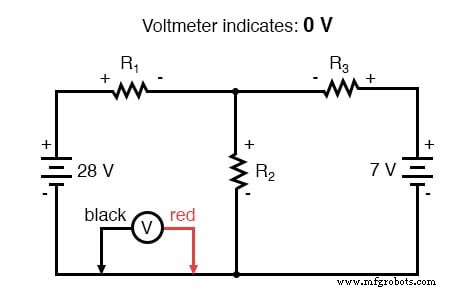
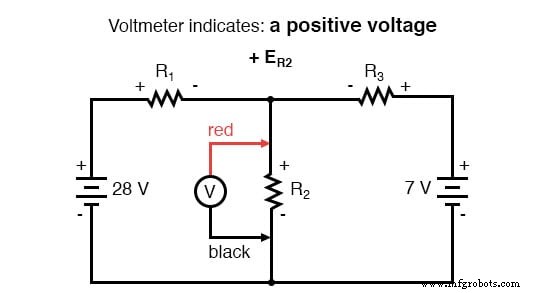
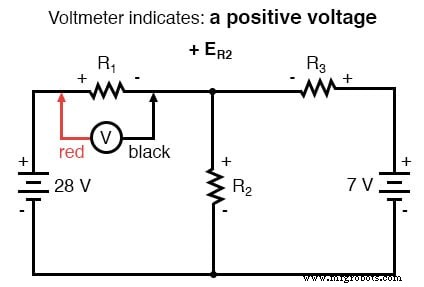
Setelah menyelesaikan jejak loop kiri kami, kami menambahkan indikasi tegangan ini bersama-sama untuk jumlah nol:

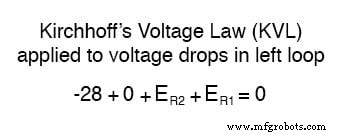
Tentu saja, kami belum mengetahui tegangan pada R₁ atau R₂ , jadi kami tidak dapat memasukkan nilai tersebut ke dalam persamaan sebagai angka numerik pada saat ini. Namun, kami melakukannya tahu bahwa ketiga tegangan harus secara aljabar ditambahkan ke nol, sehingga persamaannya benar. Kita dapat melangkah lebih jauh dan menyatakan tegangan yang tidak diketahui sebagai produk dari arus yang tidak diketahui yang sesuai (I₁ dan saya₂ ) dan resistornya masing-masing, mengikuti Hukum Ohm (E=IR), serta menghilangkan suku 0:

Karena kita tahu nilai semua resistor dalam ohm, kita bisa mengganti angka-angka itu ke dalam persamaan untuk sedikit menyederhanakan:

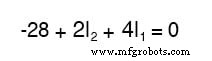
Anda mungkin bertanya-tanya mengapa kita mengalami kesulitan dalam memanipulasi persamaan ini dari bentuk awalnya (-28 + E_R2 + E_R1 ). Lagi pula, dua suku terakhir masih belum diketahui, jadi apa untungnya menyatakannya dalam tegangan yang tidak diketahui atau sebagai arus yang tidak diketahui (dikalikan dengan hambatan)? Tujuan melakukan ini adalah untuk mendapatkan persamaan KVL yang diekspresikan menggunakan variabel tidak diketahui yang sama sebagai persamaan KCL, karena ini adalah persyaratan yang diperlukan untuk setiap metode solusi persamaan simultan. Untuk memecahkan tiga arus yang tidak diketahui (I₁ , saya₂ , dan saya₃ ), kita harus memiliki tiga persamaan yang menghubungkan ketiga arus (bukan tegangan !) bersama.

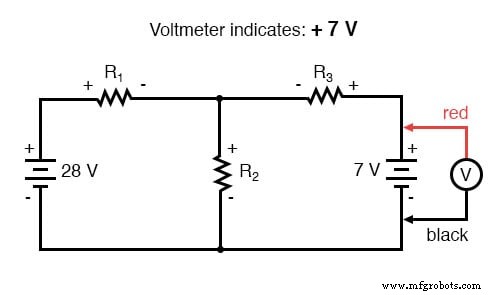
Menerapkan langkah yang sama ke loop kanan sirkuit (mulai dari node yang dipilih dan bergerak berlawanan arah jarum jam), kita mendapatkan persamaan KVL lain:

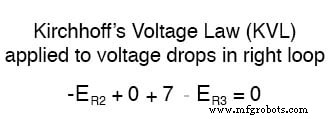
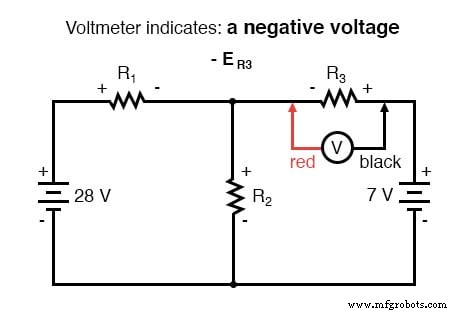
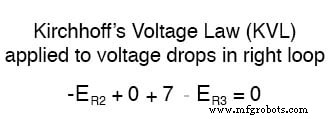
Mengetahui sekarang bahwa tegangan pada setiap resistor dapat dan seharusnya dinyatakan sebagai produk dari arus yang sesuai dan resistansi (yang diketahui) dari masing-masing resistor, kita dapat menulis ulang persamaan sebagai berikut:

Memecahkan Masalah yang Tidak Diketahui

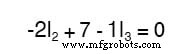
Sekarang kita memiliki sistem matematika dari tiga persamaan (satu persamaan KCL dan dua persamaan KVL) dan tiga yang tidak diketahui:

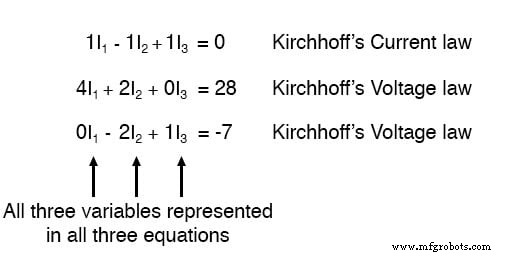
Untuk beberapa metode penyelesaian (terutama metode apa pun yang melibatkan kalkulator), akan sangat membantu untuk menyatakan setiap suku yang tidak diketahui dalam setiap persamaan, dengan nilai konstan apa pun di sebelah kanan tanda sama dengan, dan dengan suku "kesatuan" apa pun yang dinyatakan dengan koefisien eksplisit dari 1. Menulis ulang persamaan lagi, kita mendapatkan:

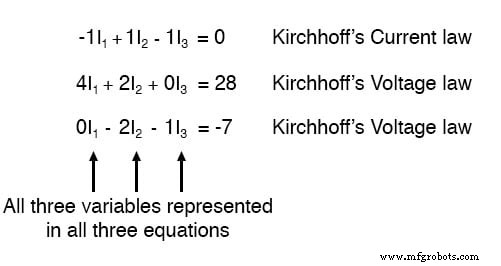
Dengan menggunakan teknik solusi apa pun yang tersedia bagi kita, kita harus sampai pada solusi untuk tiga nilai arus yang tidak diketahui:

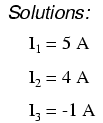
Jadi, saya₁ adalah 5 amp, saya₂ adalah 4 amp, dan saya₃ adalah 1 amp negatif. Tapi apa artinya arus "negatif"? Dalam hal ini, itu berarti asumsi kami arah untuk I₃ adalah kebalikan dari nyata arah. Kembali ke sirkuit awal, kita dapat menggambar ulang panah saat ini untuk I₃ (dan gambar ulang polaritas R₃ penurunan tegangan yang sesuai):

Gambar Ulang Sirkuit

Perhatikan bagaimana arus didorong mundur melalui baterai 2 (elektron mengalir “naik”) karena tegangan baterai 1 yang lebih tinggi (yang arusnya mengarah “turun” seperti biasanya)! Terlepas dari kenyataan bahwa polaritas baterai B2 mencoba untuk mendorong elektron ke bawah di cabang sirkuit itu, elektron dipaksa kembali melaluinya karena tegangan superior baterai B1. Apakah ini berarti bahwa baterai yang lebih kuat akan selalu "menang" dan baterai yang lebih lemah selalu mendapatkan arus yang dipaksa melaluinya ke belakang? Tidak! Ini sebenarnya tergantung pada tegangan relatif baterai dan nilai resistor pada rangkaian. Satu-satunya cara pasti untuk menentukan apa yang terjadi adalah dengan meluangkan waktu untuk menganalisis jaringan secara matematis.

Hitung Penurunan Tegangan Pada Semua Resistor

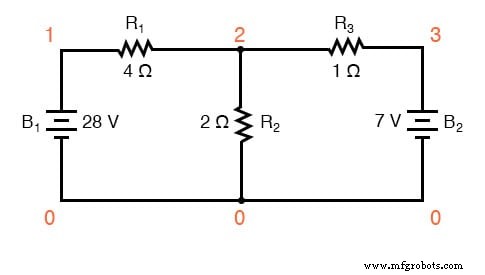
Sekarang setelah kita mengetahui besarnya semua arus dalam rangkaian ini, kita dapat menghitung penurunan tegangan pada semua resistor dengan Hukum Ohm (E=IR):

Menganalisis Jaringan Menggunakan SPICE

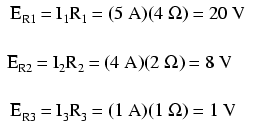
Sekarang mari kita menganalisis jaringan ini menggunakan SPICE untuk memverifikasi angka tegangan kita. Kita dapat menganalisis arus juga dengan SPICE, tetapi karena itu memerlukan penyisipan komponen tambahan ke dalam rangkaian, dan karena kita tahu bahwa jika tegangannya sama dan semua hambatannya sama, arusnya harus semuanya sama, saya akan memilih analisis yang tidak terlalu rumit. Berikut adalah gambar ulang sirkuit kami, lengkap dengan nomor simpul untuk referensi SPICE:

contoh analisis jaringan v1 1 0 v2 3 0 dc 7 r1 1 2 4 r2 2 0 2 r3 2 3 1 .dc v1 28 28 1 .cetak dc v(1,2) v(2,0) v(2,3) .akhir v1 v(1,2) v(2) v(2,3) 2.800E+01 2.000E+01 8.000E+00 1.000E+00 

Benar saja, semua angka tegangan menjadi sama:20 volt melintasi R₁ (simpul 1 dan 2), 8 volt melintasi R₂ (simpul 2 dan 0), dan 1 volt melintasi R₃ (simpul 2 dan 3). Perhatikan tanda-tanda dari semua angka tegangan ini:semuanya bernilai positif! SPICE mendasarkan polaritasnya pada urutan di mana node terdaftar, node pertama menjadi positif dan node kedua-negatif. Misalnya, angka positif (+) 20 volt antara node 1 dan 2 berarti bahwa node 1 positif terhadap node 2. Jika angka tersebut keluar negatif dalam analisis SPICE, kita akan tahu bahwa polaritas kita yang sebenarnya adalah "mundur" (simpul 1 negatif sehubungan dengan simpul 2). Memeriksa urutan node dalam daftar SPICE, kita dapat melihat bahwa semua polaritas cocok dengan apa yang kita tentukan melalui metode analisis Branch Current.

TINJAUAN:

• Langkah-langkah yang harus diikuti untuk metode analisis “Arus Cabang”:
  • Pilih simpul dan asumsikan arah arus.
  • Tuliskan persamaan KCL yang menghubungkan arus pada simpul tersebut.
  • Beri label polaritas penurunan tegangan resistor berdasarkan arus yang diasumsikan.
  • Tulis persamaan KVL untuk setiap loop rangkaian, substitusikan produk IR untuk E di setiap suku resistor persamaan.
  • Pecahkan untuk arus cabang yang tidak diketahui (persamaan simultan).
  • Jika ada solusi yang negatif, maka asumsi arah arus untuk solusi tersebut salah!
  • Atasi penurunan tegangan di semua resistor (E=IR).

LEMBAR KERJA TERKAIT:

• Lembar Kerja Analisis Arus Cabang DC