-Y dan Y-Δ Konversi

Dalam banyak aplikasi rangkaian, kita menemukan komponen yang terhubung bersama dalam salah satu dari dua cara untuk membentuk jaringan tiga terminal:konfigurasi "Delta," atau (juga dikenal sebagai "Pi," atau ), dan "Y" ( juga dikenal sebagai konfigurasi “T”).

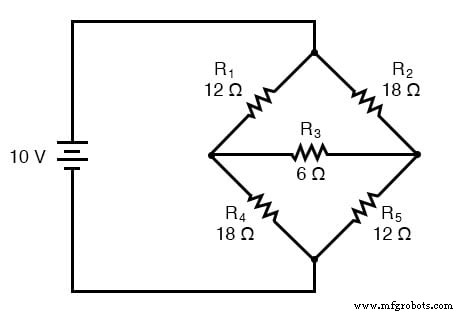
Dimungkinkan untuk menghitung nilai resistor yang tepat yang diperlukan untuk membentuk satu jenis jaringan (Δ atau Y) yang berperilaku identik dengan jenis lainnya, seperti yang dianalisis dari koneksi terminal saja. Artinya, jika kita memiliki dua jaringan resistor terpisah, satu dan satu Y, masing-masing dengan resistornya tersembunyi dari pandangan, dengan hanya tiga terminal (A, B, dan C) yang terbuka untuk pengujian, resistor dapat diukur untuk dua jaringan sehingga tidak ada cara untuk secara elektrik menentukan satu jaringan terpisah dari yang lain. Dengan kata lain, jaringan dan Y yang setara berperilaku identik.

Δ dan Persamaan Konversi Y

Ada beberapa persamaan yang digunakan untuk mengonversi satu jaringan ke jaringan lainnya:

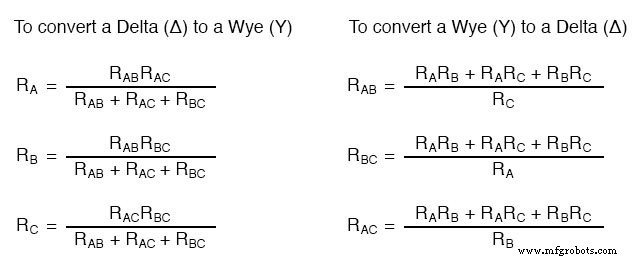
Jaringan dan Y sering terlihat dalam sistem daya AC 3-fase (topik yang dibahas dalam volume II seri buku ini), tetapi meskipun demikian, jaringan tersebut biasanya merupakan jaringan yang seimbang (semua resistor nilainya sama) dan konversi dari satu ke yang lain tidak perlu melibatkan perhitungan rumit seperti itu. Kapan rata-rata teknisi perlu menggunakan persamaan ini?

Penerapan Konversi dan Y

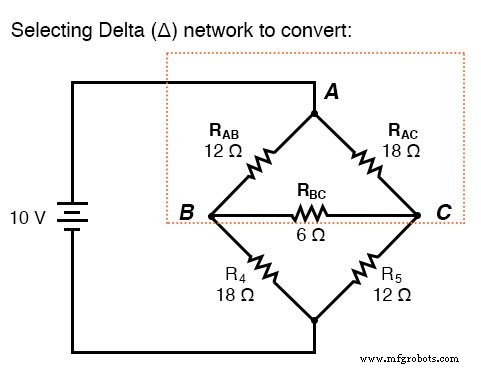
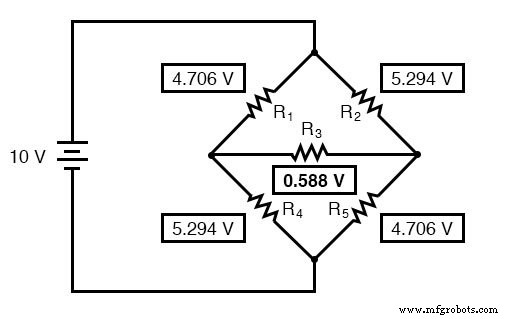
Aplikasi utama untuk konversi -Y adalah dalam solusi rangkaian jembatan tidak seimbang, seperti di bawah ini:

Solusi dari rangkaian ini dengan analisis Arus Cabang atau Arus Mesh cukup terlibat, dan baik Teorema Millman maupun Superposisi tidak membantu karena hanya ada satu sumber daya. Kita bisa menggunakan Teorema Thevenin atau Norton, memperlakukan R₃ sebagai beban kita, tapi apa itu menyenangkan?

Jika kita memperlakukan resistor R₁ , R₂ , dan R₃ sebagai terhubung dalam konfigurasi (R_ab , R_ac , dan R_bc , masing-masing) dan menghasilkan jaringan Y yang setara untuk menggantikannya, kita dapat mengubah rangkaian jembatan ini menjadi rangkaian kombinasi seri/paralel (lebih sederhana):

Setelah konversi -Y . . .

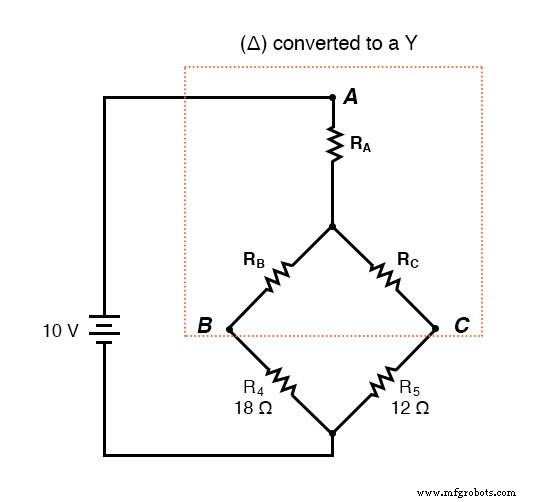
Jika kita melakukan perhitungan dengan benar, tegangan antara titik A, B, dan C akan sama di sirkuit yang dikonversi seperti di sirkuit asli, dan kita dapat mentransfer nilai-nilai itu kembali ke konfigurasi jembatan asli.

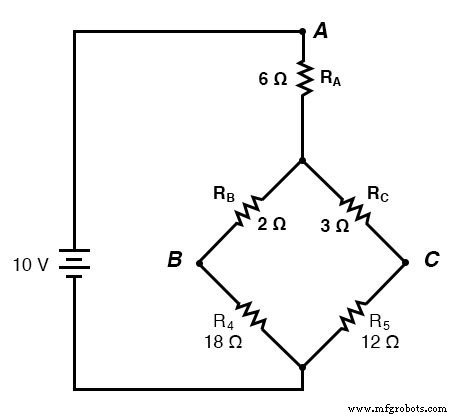
Resistor R₄ dan R₅ , tentu saja, tetap sama pada 18 dan 12 , masing-masing. Menganalisis rangkaian sekarang sebagai kombinasi seri/paralel, kita sampai pada gambar berikut:

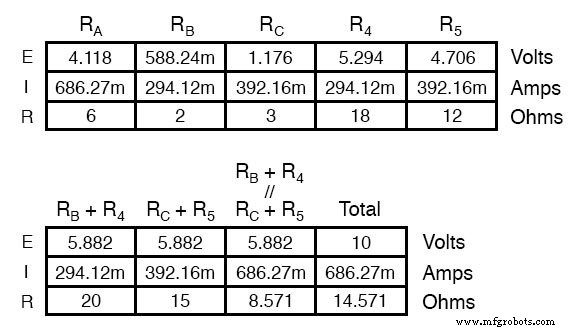
Kita harus menggunakan angka penurunan tegangan dari tabel di atas untuk menentukan tegangan antara titik A, B, dan C, dengan melihat bagaimana mereka dijumlahkan (atau dikurangi, seperti halnya dengan tegangan antara titik B dan C):

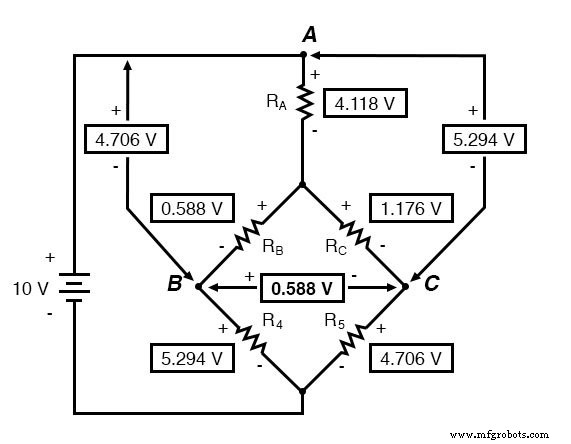
Sekarang kita mengetahui tegangan ini, kita dapat mentransfernya ke titik yang sama A, B, dan C di rangkaian jembatan asli:

Tegangan turun di R₄ dan R₅ , tentu saja, sama persis dengan rangkaian konverter.

Pada titik ini, kita dapat mengambil tegangan ini dan menentukan arus resistor melalui penggunaan berulang Hukum Ohm (I=E/R):

Simulasi Menggunakan SPICE

Simulasi cepat dengan SPICE akan berfungsi untuk memverifikasi pekerjaan kami:

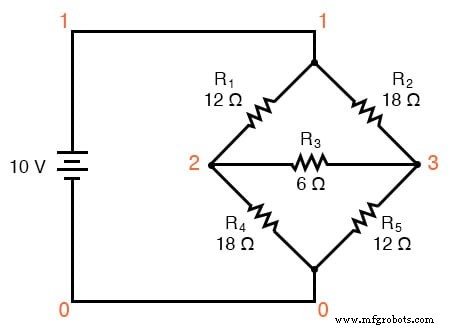
sirkuit jembatan tidak seimbang v1 1 0 r1 1 2 12 r2 1 3 18 r3 2 3 6 r4 2 0 18 r5 3 0 12 .dc v1 10 10 1 .cetak dc v(1,2) v(1,3) v(2,3) v(2,0) v(3,0) .akhir v1 v(1,2) v(1,3) v(2,3) v(2) v(3) 1.000E+01 4.706E+00 5.294E+00 5.882E-01 5.294E+00 4.706E+00 

Angka tegangan, seperti yang dibaca dari kiri ke kanan, menunjukkan penurunan tegangan pada lima resistor masing-masing, R₁ melalui R₅ . Saya bisa saja menunjukkan arus juga, tetapi karena itu akan membutuhkan penyisipan sumber tegangan "dummy" di netlist SPICE, dan karena kami terutama tertarik untuk memvalidasi persamaan konversi -Y dan bukan Hukum Ohm, ini sudah cukup.

TINJAUAN:

• Jaringan “Delta” (Δ) juga dikenal sebagai jaringan “Pi” (π).
• Jaringan “Y” juga dikenal sebagai jaringan “T”.
• Jaringan Δ dan Y dapat dikonversi ke jaringan setaranya dengan persamaan resistansi yang tepat. Dengan “setara”, maksud saya kedua jaringan akan identik secara elektrik yang diukur dari tiga terminal (A, B, dan C).
• Rangkaian jembatan dapat disederhanakan menjadi rangkaian seri/paralel dengan mengubah setengahnya dari jaringan ke jaringan Y. Setelah penurunan tegangan antara tiga titik koneksi awal (A, B, dan C) telah diselesaikan, tegangan tersebut dapat ditransfer kembali ke rangkaian jembatan asli, melalui titik ekivalen yang sama.

LEMBAR KERJA TERKAIT:

• Lembar Kerja Sirkuit 3-Fase Delta dan Wye