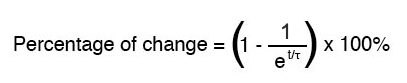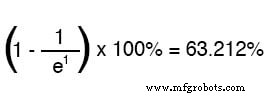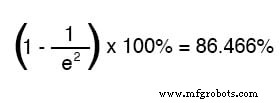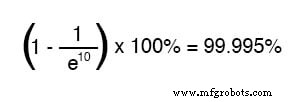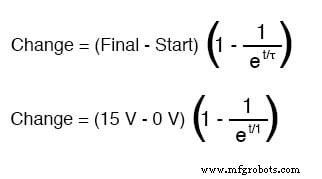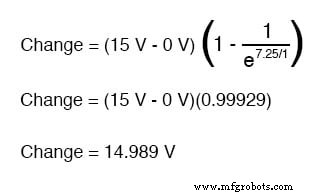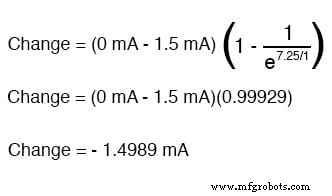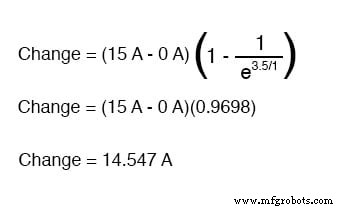Perhitungan Tegangan dan Arus

Ada cara pasti untuk menghitung nilai apa pun dalam rangkaian DC reaktif dari waktu ke waktu.

Menghitung Nilai dalam Rangkaian DC Reaktif

Langkah pertama adalah mengidentifikasi nilai awal dan akhir untuk kuantitas apa pun yang ditentang kapasitor atau induktor terhadap perubahan; yaitu, berapa pun kuantitas yang coba dipertahankan oleh komponen reaktif. Untuk kapasitor, besaran ini adalah tegangan; untuk induktor, kuantitas ini adalah arus . Ketika sakelar dalam rangkaian ditutup (atau dibuka), komponen reaktif akan berusaha mempertahankan kuantitas itu pada tingkat yang sama seperti sebelum transisi sakelar, sehingga nilai akan digunakan untuk nilai "awal".

Nilai akhir untuk kuantitas ini adalah berapa pun kuantitas itu setelah waktu yang tak terbatas. Ini dapat ditentukan dengan menganalisis rangkaian kapasitif seolah-olah kapasitor adalah rangkaian terbuka, dan rangkaian induktif seolah-olah induktor adalah hubungan pendek karena itulah yang berperilaku komponen ini ketika mereka telah mencapai "muatan penuh," setelah waktu yang tak terbatas.

Langkah selanjutnya adalah menghitung konstanta waktu sirkuit:jumlah waktu yang diperlukan untuk nilai tegangan atau arus untuk mengubah sekitar 63 persen dari nilai awal ke nilai akhir dalam situasi transien.

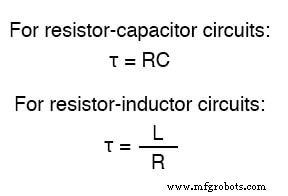
Dalam rangkaian RC seri, konstanta waktu sama dengan hambatan total dalam ohm dikalikan dengan kapasitansi total dalam farad. Untuk rangkaian L/R seri, itu adalah induktansi total dalam henrys dibagi dengan resistansi total dalam ohm. Dalam kedua kasus, konstanta waktu dinyatakan dalam satuan detik dan dilambangkan dengan huruf Yunani “tau” (τ):

Naik turunnya nilai rangkaian seperti tegangan dan arus sebagai respons terhadap transien, seperti yang telah disebutkan sebelumnya, asimptotik . Karena itu, nilai-nilai mulai berubah dengan cepat segera setelah transien dan menetap seiring waktu. Jika diplot pada grafik, pendekatan ke nilai akhir tegangan dan arus membentuk kurva eksponensial.

Seperti yang dinyatakan sebelumnya, satu konstanta waktu adalah jumlah waktu yang diperlukan untuk salah satu dari nilai-nilai ini untuk berubah sekitar 63 persen dari nilai awal ke nilai akhir (akhir). Untuk setiap waktu yang konstan, nilai-nilai ini bergerak (kurang lebih) 63 persen lebih dekat ke tujuan akhirnya. Rumus matematika untuk menentukan persentase yang tepat cukup sederhana:

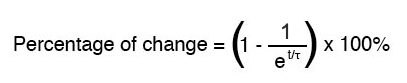
Surat e singkatan dari konstanta Euler, yaitu sekitar 2,7182818. Ini berasal dari teknik kalkulus, setelah secara matematis menganalisis pendekatan asimtotik dari nilai rangkaian. Setelah nilai waktu konstan satu kali, persentase perubahan dari nilai awal ke nilai akhir adalah:

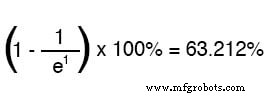
Setelah nilai waktu dua konstanta waktu, persentase perubahan dari nilai awal ke nilai akhir adalah:

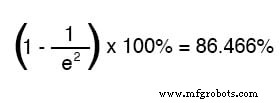
Setelah waktu sepuluh konstanta waktu, persentasenya adalah:

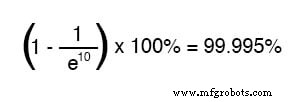
Semakin banyak waktu yang berlalu sejak penerapan tegangan sementara dari baterai, semakin besar nilai penyebut dalam pecahan, yang membuat nilai yang lebih kecil untuk seluruh pecahan, yang membuat total keseluruhan (1 dikurangi pecahan) mendekati 1, atau 100 persen.

Rumus Konstanta Waktu Universal

Kita dapat membuat rumus yang lebih universal dari rumus ini untuk penentuan nilai tegangan dan arus dalam rangkaian transien, dengan mengalikan besaran ini dengan selisih antara nilai rangkaian akhir dan awal:

Mari kita analisis kenaikan tegangan pada rangkaian resistor-kapasitor seri yang ditunjukkan pada awal bab ini.

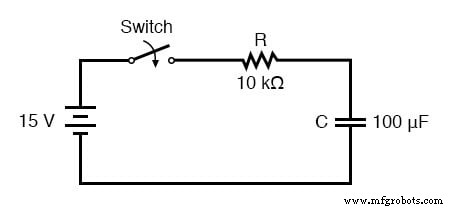
Perhatikan bahwa kami memilih untuk menganalisis tegangan karena itulah jumlah kapasitor yang cenderung konstan. Meskipun rumus bekerja cukup baik untuk arus, nilai awal dan akhir untuk arus sebenarnya diturunkan dari tegangan kapasitor, jadi penghitungan tegangan adalah metode yang lebih langsung. Resistansinya adalah 10 kΩ, dan kapasitansinya adalah 100 F (mikrofarad). Karena konstanta waktu (τ) untuk rangkaian RC adalah produk dari resistansi dan kapasitansi, kami memperoleh nilai 1 detik:

Jika kapasitor mulai dalam keadaan kosong total (0 volt), maka kita dapat menggunakan nilai tegangan tersebut untuk nilai "awal". Nilai akhir, tentu saja, adalah tegangan baterai (15 volt). Rumus universal kami untuk tegangan kapasitor di sirkuit ini terlihat seperti ini:

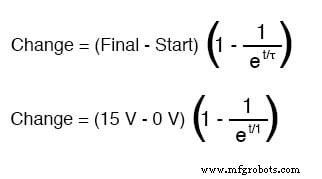
Jadi, setelah 7,25 detik menerapkan tegangan melalui sakelar tertutup, tegangan kapasitor kita akan meningkat sebesar:

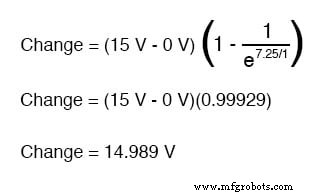
Karena kita mulai dengan tegangan kapasitor 0 volt, peningkatan 14,899 volt ini berarti bahwa kita memiliki 14,899 volt setelah 7,25 detik.

Rumus yang sama akan bekerja untuk menentukan arus di sirkuit itu juga. Karena kita tahu bahwa kapasitor yang dikosongkan awalnya bertindak seperti korsleting, arus awal akan menjadi jumlah maksimum yang mungkin:15 volt (dari baterai) dibagi dengan 10 kΩ (satu-satunya oposisi terhadap arus di sirkuit di awal):

Kita juga tahu bahwa arus akhir akan menjadi nol, karena kapasitor pada akhirnya akan berperilaku sebagai rangkaian terbuka, yang berarti bahwa pada akhirnya, tidak ada elektron yang akan mengalir dalam rangkaian. Sekarang setelah kita mengetahui nilai arus awal dan akhir, kita dapat menggunakan rumus universal untuk menentukan arus setelah 7,25 detik penutupan sakelar di sirkuit RC yang sama:

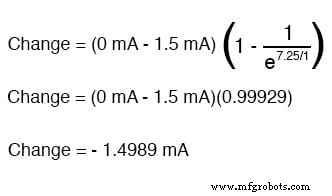
Perhatikan bahwa angka yang diperoleh untuk perubahan adalah negatif, bukan positif! Ini memberitahu kita bahwa arus telah berkurang bukannya meningkat seiring berjalannya waktu. Karena kita memulai pada arus 1,5 mA, penurunan ini (-1,4989 mA) berarti kita memiliki 0,001065 mA (1,065 A) setelah 7,25 detik.

Kita juga dapat menentukan arus rangkaian pada waktu=7,25 detik dengan mengurangkan tegangan kapasitor (14,899 volt) dari tegangan baterai (15 volt) untuk mendapatkan penurunan tegangan pada resistor 10 kΩ, kemudian menghitung arus yang melalui resistor (dan seluruh rangkaian seri) dengan Hukum Ohm (I=E/R). Bagaimanapun, kita harus mendapatkan jawaban yang sama:

Menggunakan Rumus Konstanta Waktu Universal untuk Menganalisis Rangkaian Induktif

Rumus konstanta waktu universal juga bekerja dengan baik untuk menganalisis rangkaian induktif. Mari kita terapkan pada contoh rangkaian L/R kita di awal bab ini:

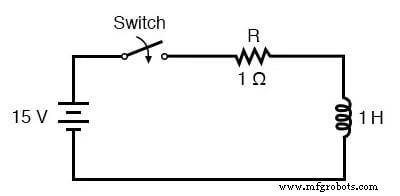
Dengan induktansi 1 henry dan hambatan seri 1 , konstanta waktu kita sama dengan 1 detik:

Karena ini adalah rangkaian induktif, dan kita tahu bahwa induktor menentang perubahan arus, kita akan membuat rumus konstanta waktu untuk nilai awal dan nilai akhir arus. Jika kita memulai dengan sakelar dalam posisi terbuka, arus akan sama dengan nol, jadi nol adalah nilai arus awal kita.

Setelah sakelar dibiarkan tertutup untuk waktu yang lama, arus akan turun ke nilai akhirnya, sama dengan tegangan sumber dibagi dengan resistansi rangkaian total (I=E/R), atau 15 amp dalam kasus rangkaian ini .

Jika kita ingin menentukan nilai arus pada 3,5 detik, kita akan menerapkan rumus konstanta waktu universal seperti ini:

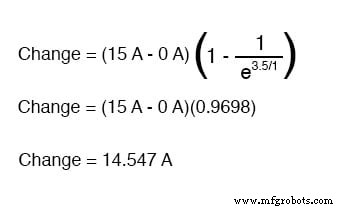
Mengingat fakta bahwa arus awal kami adalah nol, ini membuat kami pada arus rangkaian 14,547 amp pada waktu 3,5 detik.

Menentukan tegangan dalam rangkaian induktif paling baik dilakukan dengan terlebih dahulu mencari arus rangkaian dan kemudian menghitung penurunan tegangan melintasi resistansi untuk menemukan apa yang tersisa untuk jatuh melintasi induktor. Dengan hanya satu resistor di rangkaian contoh kami (memiliki nilai 1 ), ini agak mudah:

Dikurangi dari tegangan baterai 15 volt, ini menyisakan 0,453 volt melintasi induktor pada waktu=3,5 detik.

TINJAUAN:

• Rumus Konstanta Waktu Universal:
• Untuk menganalisis rangkaian RC atau L/R, ikuti langkah-langkah berikut:
• (1):Tentukan konstanta waktu untuk rangkaian (RC atau L/R).
• (2):Identifikasi besaran yang akan dihitung (jumlah apa pun yang perubahannya secara langsung ditentang oleh komponen reaktif. Untuk kapasitor ini adalah tegangan; untuk induktor ini adalah arus).
• (3):Tentukan nilai awal dan akhir untuk besaran tersebut.
• (4):Masukkan semua nilai ini (Akhir, Mulai, waktu, konstanta waktu) ke dalam rumus konstanta waktu universal dan selesaikan perubahan dalam jumlah.
• (5):Jika nilai awalnya adalah nol, maka nilai sebenarnya pada waktu yang ditentukan sama dengan perubahan yang dihitung yang diberikan oleh rumus universal. Jika tidak, tambahkan perubahan ke nilai awal untuk mengetahui di mana Anda berada.

LEMBAR KERJA TERKAIT:

• Lembar Kerja Sirkuit Konstanta Waktu
• Lembar Kerja Perhitungan Konstanta Waktu

Lihat koleksi . kami Kalkulator Daya di . kami Alat bagian.