Teknologi Industri








Pada bagian sebelumnya, kita telah mengeksplorasi apa yang akan terjadi pada rangkaian AC sederhana yang hanya terdiri dari resistor dan hanya induktor. Sekarang kita akan menggabungkan kedua komponen tersebut dalam bentuk seri dan menyelidiki efeknya.
Ambil sirkuit ini sebagai contoh untuk bekerja dengan:
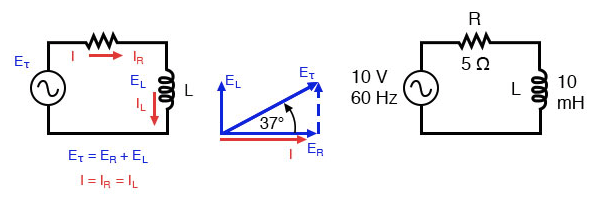
Rangkaian induktor resistor seri:Arus tertinggal dari tegangan yang diberikan sebesar 0o hingga 90o.
Resistor akan menawarkan 5 resistansi terhadap arus AC terlepas dari frekuensinya, sedangkan induktor akan menawarkan 3,7699 reaktansi terhadap arus AC pada 60 Hz.
Karena hambatan resistor adalah bilangan real (5 0°, atau 5 + j0 ), dan reaktansi induktor adalah bilangan imajiner (3,7699 90°, atau 0 + j3,7699 ), efek gabungan dari dua komponen akan berlawanan dengan arus yang sama dengan jumlah kompleks kedua bilangan tersebut.
Oposisi gabungan ini akan menjadi kombinasi vektor resistensi dan reaktansi. Untuk mengekspresikan oposisi ini secara ringkas, kita memerlukan istilah yang lebih komprehensif untuk oposisi terhadap arus daripada resistansi atau reaktansi saja.
Istilah ini disebut impedansi , simbolnya adalah Z, dan juga dinyatakan dalam satuan ohm, seperti resistansi dan reaktansi. Dalam contoh di atas, impedansi rangkaian total adalah:

Impedansi terkait dengan tegangan dan arus seperti yang Anda duga, dengan cara yang mirip dengan resistansi dalam Hukum Ohm:

Faktanya, ini adalah bentuk Hukum Ohm yang jauh lebih komprehensif daripada apa yang diajarkan dalam elektronik DC (E =IR), sama seperti impedansi adalah ekspresi oposisi terhadap aliran arus yang jauh lebih komprehensif daripada resistansi. Apa saja resistansi dan reaktansi apapun, secara terpisah atau dalam kombinasi (seri/paralel), dapat dan harus direpresentasikan sebagai impedansi tunggal dalam rangkaian AC.
Untuk menghitung arus pada rangkaian di atas, pertama-tama kita perlu memberikan referensi sudut fasa untuk sumber tegangan, yang umumnya diasumsikan nol. (Sudut fase impedansi resistif dan induktif selalu 0 ° dan +90 °, masing-masing, terlepas dari sudut fase yang diberikan untuk tegangan atau arus).
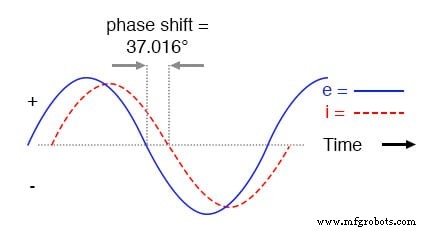
Seperti pada rangkaian induktif murni, gelombang arus tertinggal di belakang gelombang tegangan (dari sumber), meskipun kali ini kelambatannya tidak sebesar:hanya 37,016° dibandingkan dengan 90° penuh seperti yang terjadi pada rangkaian induktif murni. .

Arus tertinggal dari tegangan dalam rangkaian L-R seri.
Untuk resistor dan induktor, hubungan fase antara tegangan dan arus tidak berubah. Tegangan melintasi resistor berada dalam fase (pergeseran 0°) dengan arus yang melaluinya, dan tegangan melintasi induktor adalah +90° di luar fase dengan arus yang melewatinya. Kami dapat memverifikasi ini secara matematis:

Tegangan melintasi resistor memiliki sudut fasa yang sama persis dengan arus yang melaluinya, memberi tahu kita bahwa E dan I berada dalam fasa (hanya untuk resistor).

Tegangan melintasi induktor memiliki sudut fasa 52,984°, sedangkan arus yang melalui induktor memiliki sudut fasa -37.016°, perbedaan antara keduanya tepat 90°. Ini memberitahu kita bahwa E dan I masih berada di luar fase 90° (hanya untuk induktor).
Kita juga dapat membuktikan secara matematis bahwa nilai kompleks ini dijumlahkan untuk menghasilkan tegangan total, seperti yang diprediksi oleh Hukum Tegangan Kirchhoff:

Mari kita periksa validitas perhitungan kita dengan SPICE:
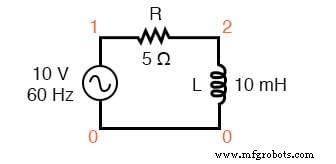
v1 1 0 ac 10 sin r1 1 2 5 l1 2 0 10m .ac lin 1 60 60 .cetak ac v(1,2) v(2,0) i(v1) .cetak ac vp(1,2) vp(2,0) ip(v1) .akhir

Perhatikan bahwa seperti halnya sirkuit DC, SPICE mengeluarkan angka arus seolah-olah mereka negatif (di luar fase 180 °) dengan tegangan suplai. Alih-alih sudut fase -37.016°, kami mendapatkan sudut fase saat ini 143°(-37° + 180°).
Ini hanyalah keistimewaan SPICE dan tidak mewakili sesuatu yang signifikan dalam simulasi rangkaian itu sendiri. Perhatikan bagaimana pembacaan fase tegangan resistor dan induktor cocok dengan perhitungan kami (masing-masing -37,02° dan 52,98°), seperti yang kami harapkan.
Dengan semua angka ini untuk dilacak bahkan untuk rangkaian sederhana seperti ini, akan bermanfaat bagi kita untuk menggunakan metode "tabel". Menerapkan tabel ke rangkaian resistor-induktor seri sederhana ini akan berjalan seperti itu.
Pertama, buat tabel untuk gambar E/I/Z dan masukkan semua nilai komponen dalam istilah ini (dengan kata lain, jangan masukkan nilai resistansi atau induktansi aktual dalam ohm dan henri, masing-masing, ke dalam tabel; alih-alih, konversikan ke dalam angka impedansi kompleks dan tuliskan dalam):
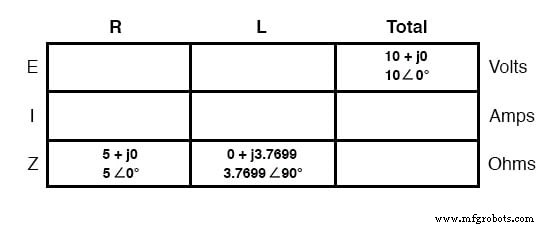
Meskipun tidak perlu, saya merasa terbantu untuk menulis keduanya bentuk persegi panjang dan kutub dari setiap kuantitas dalam tabel. Jika Anda menggunakan kalkulator yang memiliki kemampuan untuk melakukan aritmatika kompleks tanpa memerlukan konversi antara bentuk persegi dan kutub, maka dokumentasi tambahan ini sama sekali tidak diperlukan.
Namun, jika Anda dipaksa untuk melakukan aritmatika yang kompleks "tangan" (penjumlahan dan pengurangan dalam bentuk persegi panjang, dan perkalian dan pembagian dalam bentuk kutub), menulis setiap kuantitas dalam kedua bentuk akan sangat berguna.
Sekarang angka "yang diberikan" kami dimasukkan ke dalam lokasi masing-masing dalam tabel, kami dapat melanjutkan seperti dengan DC:tentukan total impedansi dari masing-masing impedansi. Karena ini adalah rangkaian seri, kita tahu bahwa oposisi terhadap aliran arus (hambatan atau impedansi) menambah membentuk oposisi total:
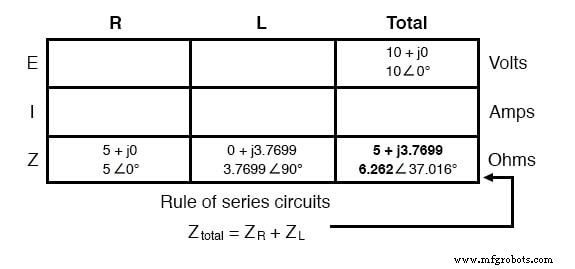
Sekarang setelah kita mengetahui tegangan total dan impedansi total, kita dapat menerapkan Hukum Ohm (I=E/Z) untuk menentukan arus total:
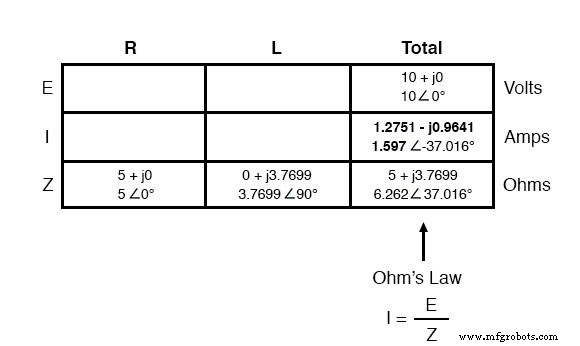
Sama seperti DC, arus total dalam rangkaian AC seri dibagi rata oleh semua komponen. Ini masih benar karena dalam rangkaian seri hanya ada satu jalur untuk arus mengalir, oleh karena itu laju alirannya harus seragam di seluruh. Akibatnya, kita dapat mentransfer angka arus ke dalam kolom untuk resistor dan induktor sama:
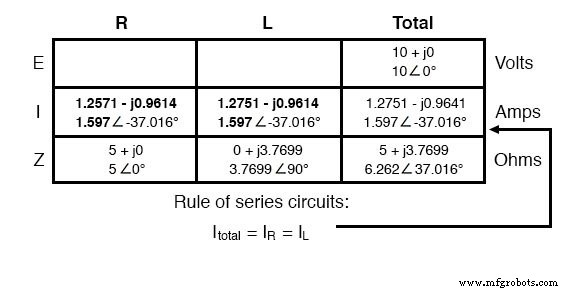
Sekarang yang tersisa untuk dihitung adalah penurunan tegangan pada resistor dan induktor, masing-masing. Ini dilakukan melalui penggunaan Hukum Ohm (E=IZ), diterapkan secara vertikal di setiap kolom tabel:
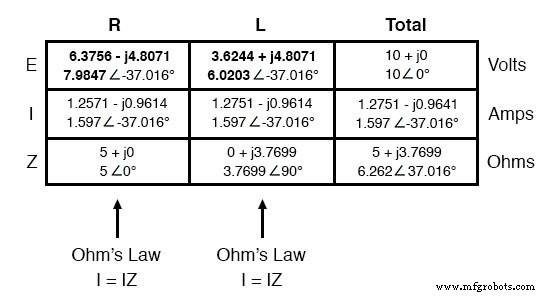
Dan dengan itu, meja kami selesai. Aturan yang sama persis yang kami terapkan dalam analisis rangkaian DC juga berlaku untuk rangkaian AC, dengan peringatan bahwa semua besaran harus direpresentasikan dan dihitung dalam bentuk kompleks dan bukan skalar.
Selama pergeseran fasa terwakili dengan benar dalam perhitungan kami, tidak ada perbedaan mendasar dalam cara kami mendekati analisis rangkaian AC dasar versus DC.
Sekarang adalah saat yang tepat untuk meninjau hubungan antara angka-angka yang dihitung ini dan pembacaan yang diberikan oleh pengukuran instrumen aktual dari tegangan dan arus.
Angka-angka di sini yang secara langsung berhubungan dengan pengukuran kehidupan nyata adalah dalam notasi kutub , bukan persegi panjang! Dengan kata lain, jika Anda menghubungkan voltmeter melintasi resistor di sirkuit ini, itu akan menunjukkan 7,9847 volt, bukan 6,3756 (persegi panjang nyata) atau 4,8071 (persegi panjang imajiner).
Untuk menggambarkan hal ini dalam istilah grafis, instrumen pengukuran hanya memberi tahu Anda berapa lama vektor untuk kuantitas tertentu (tegangan atau arus).
Notasi persegi panjang, sementara nyaman untuk penambahan dan pengurangan aritmatika, adalah bentuk notasi yang lebih abstrak daripada polar dalam kaitannya dengan pengukuran dunia nyata. Seperti yang saya nyatakan sebelumnya, saya akan menunjukkan bentuk kutub dan persegi panjang dari masing-masing kuantitas dalam tabel rangkaian AC saya hanya untuk kenyamanan perhitungan matematis.
Ini tidak mutlak diperlukan, tetapi mungkin bermanfaat bagi mereka yang mengikuti tanpa menggunakan kalkulator canggih. Jika kita membatasi diri pada penggunaan hanya satu bentuk notasi, pilihan terbaik adalah polar, karena itu adalah satu-satunya yang dapat dikorelasikan langsung dengan pengukuran nyata.
Impedansi (Z) dari rangkaian RL seri dapat dihitung, mengingat resistansi (R) dan reaktansi induktif (XL). Karena E=IR, E=IXL, dan E=IZ, resistansi, reaktansi, dan impedansi masing-masing sebanding dengan tegangan. Dengan demikian, diagram fasor tegangan dapat diganti dengan diagram impedansi yang serupa.
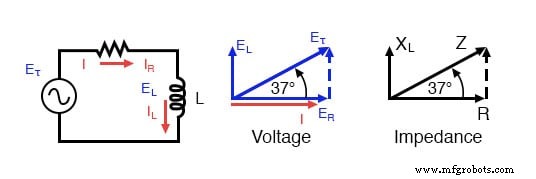
Seri:Diagram fasor impedansi rangkaian R-L.
Contoh: Diketahui:Sebuah resistor 40 dirangkai seri dengan induktor 79,58 millihenry. Temukan impedansi pada 60 hertz.
TINJAUAN:
LEMBAR KERJA TERKAIT:
Teknologi Industri
Sirkuit AC resistif murni:tegangan dan arus sefasa. Jika kita memplot arus dan tegangan untuk rangkaian AC yang sangat sederhana yang terdiri dari sumber dan resistor, (gambar di atas) akan terlihat seperti ini:(gambar di bawah) Tegangan dan arus “dalam fase” untuk rangkaian resistif. Ka
Pada bagian terakhir, kita telah mempelajari apa yang akan terjadi pada rangkaian AC sederhana yang hanya terdiri dari resistor dan kapasitor. Sekarang kita akan menggabungkan dua komponen bersama-sama dalam bentuk seri dan menyelidiki efeknya. Rangkaian kapasitor seri:tegangan tertinggal dari a
Kabel Paralel dengan Panjang Tak Terbatas Namun, seandainya kita memiliki satu set kabel paralel tak berhingga panjang, tanpa lampu di ujungnya. Apa yang akan terjadi ketika kita menutup saklar? Karena tidak ada lagi beban di ujung kabel, sirkuit ini terbuka. Apakah tidak akan ada arus sama sekali?
Pengatur arus bekerja setiap kali ponsel diisi ulang, mobil dinyalakan, komputer dicolokkan, atau peralatan listrik kecil dinyalakan. Kadang-kadang disebut pengatur tegangan, pengatur arus mengurangi dan membatasi jumlah listrik ke tingkat yang diperlukan agar perangkat listrik dapat beroperasi. Aru