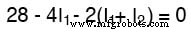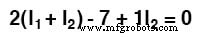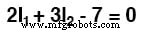Metode dan Analisis Mesh Saat Ini
Metode Mesh-Saat Ini , juga dikenal sebagai Metode Arus Loop , sangat mirip dengan metode Arus Cabang karena menggunakan persamaan simultan, Hukum Tegangan Kirchhoff, dan Hukum Ohm untuk menentukan arus yang tidak diketahui dalam jaringan. Ini berbeda dari metode Branch Current karena tidak gunakan Hukum Arus Kirchhoff, dan biasanya dapat menyelesaikan rangkaian dengan variabel yang lebih sedikit dan persamaan yang kurang simultan, yang sangat bagus jika Anda terpaksa menyelesaikannya tanpa kalkulator.
Mesh Current, metode konvensional
Mari kita lihat bagaimana metode ini bekerja pada contoh masalah yang sama:
Identifikasi Loop
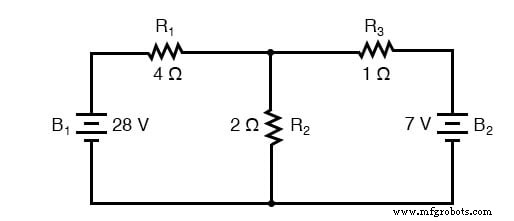
Langkah pertama dalam metode Arus Jala adalah mengidentifikasi "loop" di dalam sirkuit yang mencakup semua komponen. Dalam rangkaian contoh kami, loop yang dibentuk oleh B1 , R1 , dan R2 akan menjadi yang pertama saat loop dibentuk oleh B2 , R2 , dan R3 akan menjadi yang kedua. Bagian paling aneh dari metode Arus Jala adalah membayangkan arus yang bersirkulasi di setiap loop. Sebenarnya, metode ini mendapatkan namanya dari ide arus yang menyatu di antara loop seperti set roda gigi yang berputar:
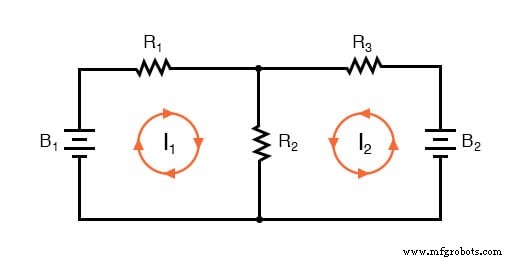
Pilihan arah masing-masing arus sepenuhnya arbitrer, seperti pada metode Arus Cabang, tetapi persamaan yang dihasilkan lebih mudah diselesaikan jika arus mengalir ke arah yang sama melalui komponen yang berpotongan (perhatikan bagaimana arus I1 dan saya2 keduanya akan "naik" melalui resistor R2 , di mana mereka "bertautan", atau berpotongan). Jika asumsi arah arus mesh salah, jawaban untuk arus tersebut akan bernilai negatif.
Beri label pada Polaritas Penurunan Tegangan
Langkah selanjutnya adalah memberi label semua polaritas penurunan tegangan pada resistor sesuai dengan arah arus mesh yang diasumsikan. Ingatlah bahwa ujung "hulu" resistor akan selalu negatif, dan ujung "hilir" resistor positif terhadap satu sama lain, karena elektron bermuatan negatif. Polaritas baterai, tentu saja, ditentukan oleh orientasi simbolnya dalam diagram, dan mungkin atau mungkin tidak "setuju" dengan polaritas resistor (asumsi arah arus):
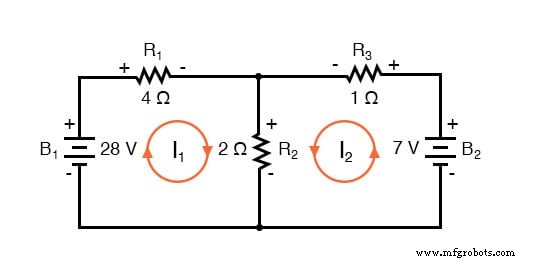
Menggunakan Hukum Tegangan Kirchhoff, sekarang kita dapat melangkah di sekitar setiap loop ini, menghasilkan persamaan yang mewakili penurunan tegangan dan polaritas komponen. Seperti metode Arus Cabang, kita akan menunjukkan penurunan tegangan resistor sebagai produk dari resistansi (dalam ohm) dan arus mesh masing-masing (jumlah itu tidak diketahui pada saat ini). Di mana dua arus menyatu, kita akan menulis istilah itu dalam persamaan dengan arus resistor menjadi jumlah dari dua arus meshing.
Menelusuri Loop Kiri Sirkuit dengan Persamaan
Menelusuri loop kiri sirkuit, mulai dari sudut kiri atas dan bergerak berlawanan arah jarum jam (pilihan titik awal dan arah pada akhirnya tidak relevan), menghitung polaritas seolah-olah kita memiliki voltmeter di tangan, timah merah di titik di depan dan timah hitam pada titik di belakang, kita mendapatkan persamaan ini:
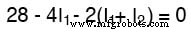
Perhatikan bahwa suku tengah persamaan menggunakan jumlah arus mesh I1 dan saya2 sebagai arus yang melalui resistor R2 . Ini karena arus mesh I1 dan saya2 menuju arah yang sama melalui R2 , dan dengan demikian saling melengkapi. Mendistribusikan koefisien 2 ke I1 dan saya2 istilah, dan kemudian menggabungkan I1 suku dalam persamaan, kita dapat menyederhanakannya sebagai berikut:

Saat ini kita memiliki satu persamaan dengan dua yang tidak diketahui. Untuk dapat menyelesaikan dua arus mesh yang tidak diketahui, kita harus memiliki dua persamaan. Jika kita menelusuri loop lain dari rangkaian, kita dapat memperoleh persamaan KVL lain dan memiliki data yang cukup untuk menyelesaikan dua arus. Makhluk kebiasaan saya, saya akan mulai di sudut kiri atas lingkaran kanan dan melacak berlawanan arah jarum jam:
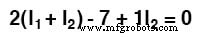
Menyederhanakan persamaan seperti sebelumnya, kita mendapatkan:
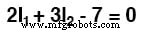
Memecahkan Masalah yang Tidak Diketahui
Sekarang, dengan dua persamaan, kita dapat menggunakan salah satu dari beberapa metode untuk menyelesaikan secara matematis arus yang tidak diketahui I1 dan saya2 :

Gambar Ulang Sirkuit
Mengetahui bahwa solusi ini adalah nilai untuk mesh arus, bukan cabang arus, kita harus kembali ke diagram kita untuk melihat bagaimana mereka cocok bersama untuk memberikan arus melalui semua komponen:
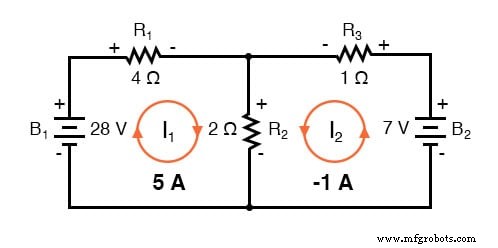
Solusi -1 amp untuk I2 berarti bahwa kami awalnya menganggap arah arus salah. Sebenarnya, saya2 mengalir berlawanan arah jarum jam pada nilai (positif) 1 amp:
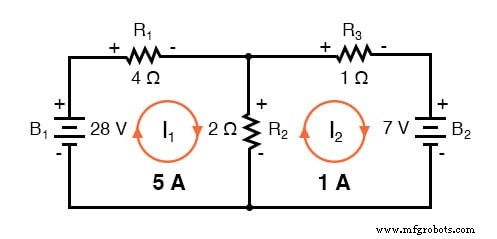
Perubahan arah arus dari yang pertama kali diasumsikan akan mengubah polaritas penurunan tegangan pada R2 dan R3 karena saat ini I2 . Dari sini, kita dapat mengatakan bahwa arus melalui R1 adalah 5 amp, dengan penurunan tegangan pada R1 menjadi produk dari arus dan hambatan (E=IR), 20 volt (positif di kiri dan negatif di kanan).
Juga, kita dapat dengan aman mengatakan bahwa arus melalui R3 adalah 1 amp, dengan drop tegangan 1 volt (E =IR), positif di sebelah kiri dan negatif di sebelah kanan. Tapi apa yang terjadi di R2 ?
Arus jala I1 akan "turun" melalui R2 , sedangkan arus mesh I2 akan "naik" melalui R2 . Untuk menentukan arus aktual melalui R2 , kita harus melihat bagaimana arus mesh I1 dan saya2 berinteraksi (dalam hal ini mereka bertentangan), dan secara aljabar menambahkan mereka untuk sampai pada nilai akhir. Sejak saya1 akan "turun" pada 5 amp, dan saya2 akan "naik" pada 1 amp, nyata arus melalui R2 harus bernilai 4 amp, akan "turun":
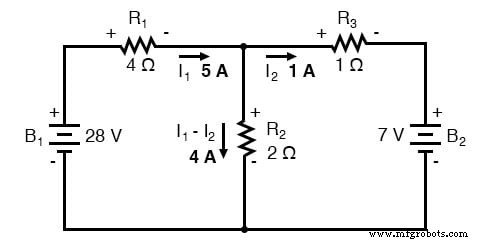
Arus 4 amp melalui R2 Resistansi 2 memberikan kita penurunan tegangan sebesar 8 volt (E=IR), positif di bagian atas dan negatif di bagian bawah.
Keuntungan Analisis Arus Mesh
Keuntungan utama dari analisis Mesh Current adalah bahwa hal itu secara umum memungkinkan untuk solusi jaringan besar dengan nilai yang tidak diketahui lebih sedikit dan persamaan simultan yang lebih sedikit. Contoh soal kita mengambil tiga persamaan untuk menyelesaikan metode Arus Cabang dan hanya dua persamaan yang menggunakan metode Arus Jala. Keuntungan ini jauh lebih besar dengan meningkatnya kompleksitas jaringan:
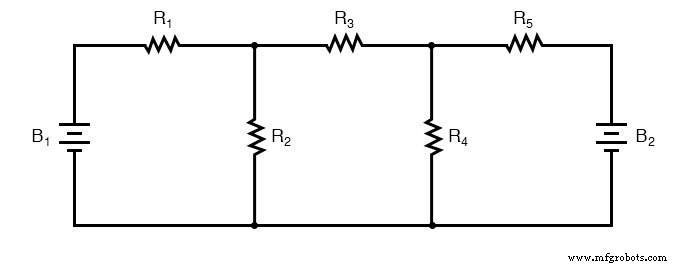
Untuk menyelesaikan jaringan ini menggunakan Arus Cabang, kita harus menetapkan lima variabel untuk memperhitungkan setiap arus unik dalam rangkaian (I1 melalui I5 ). Ini akan membutuhkan lima persamaan untuk solusinya, dalam bentuk dua persamaan KCL dan tiga persamaan KVL (dua persamaan untuk KCL di node, dan tiga persamaan untuk KVL di setiap loop):
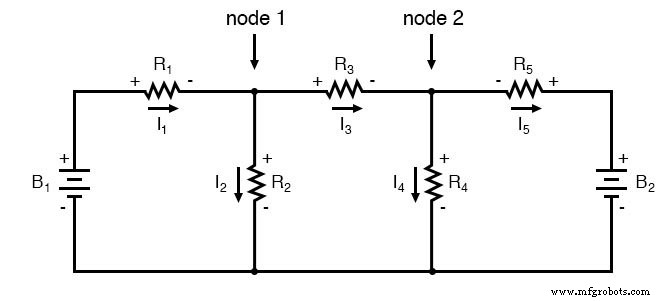
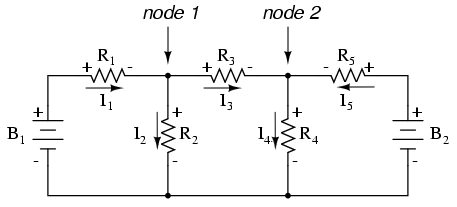

Saya kira jika Anda tidak memiliki hal yang lebih baik untuk dilakukan dengan waktu Anda selain memecahkan lima variabel yang tidak diketahui dengan lima persamaan, Anda mungkin tidak keberatan menggunakan metode analisis Arus Cabang untuk rangkaian ini. Bagi kita yang memiliki hal yang lebih baik untuk dilakukan dengan waktu kita, metode Arus Jala jauh lebih mudah, hanya membutuhkan tiga yang tidak diketahui dan tiga persamaan untuk dipecahkan:
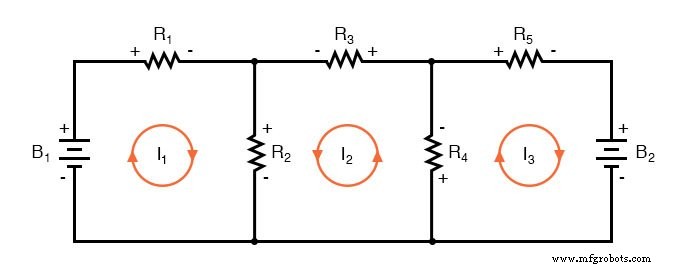
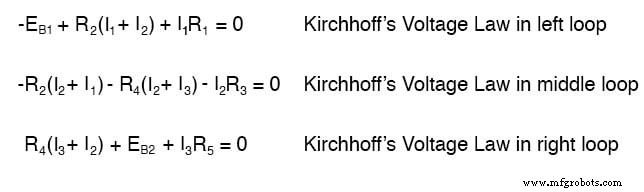
Lebih sedikit persamaan untuk dikerjakan adalah keuntungan yang pasti, terutama saat melakukan solusi persamaan simultan dengan tangan (tanpa kalkulator).
Jembatan Wheatstone Tidak Seimbang
Jenis sirkuit lain yang cocok untuk Arus Mesh adalah Jembatan Wheatstone yang tidak seimbang. Ambil sirkuit ini, misalnya:
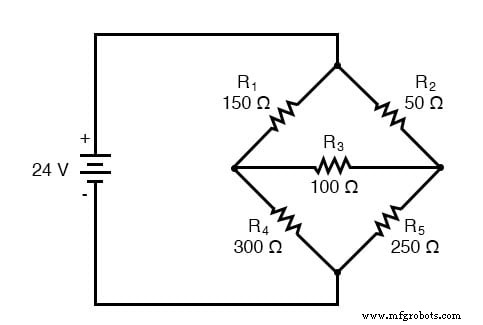
Karena rasio R1 /R4 dan R2 /R5 tidak sama, kita tahu bahwa akan ada tegangan melintasi resistor R3 , dan sejumlah arus yang melaluinya. Seperti yang dibahas di awal bab ini, jenis rangkaian ini tidak dapat direduksi dengan analisis seri-paralel normal, dan hanya dapat dianalisis dengan beberapa metode lain.
Kita bisa menerapkan metode Arus Cabang ke sirkuit ini, tetapi itu akan membutuhkan enam arus (I1 melalui I6 ), yang mengarah ke serangkaian persamaan simultan yang sangat besar untuk dipecahkan. Namun, dengan menggunakan metode Arus Jala, kita dapat menyelesaikan semua arus dan tegangan dengan variabel yang jauh lebih sedikit.
Gambar Jala
Langkah pertama dalam metode Arus Jala adalah menggambar arus jala yang cukup untuk memperhitungkan semua komponen dalam rangkaian. Melihat rangkaian jembatan kita, seharusnya jelas di mana menempatkan dua arus ini:
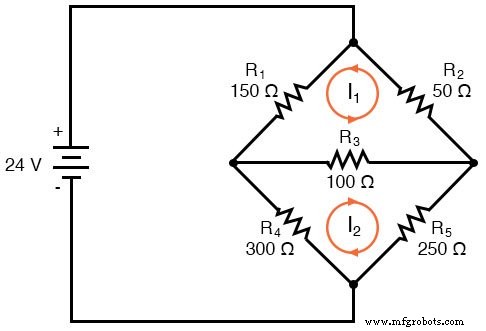
Arah arus mesh ini, tentu saja, sewenang-wenang. Namun, dua arus jala tidak cukup di sirkuit ini, karena saya1 atau saya2 melewati baterai. Jadi, kita harus menambahkan arus mesh ketiga, I3 :
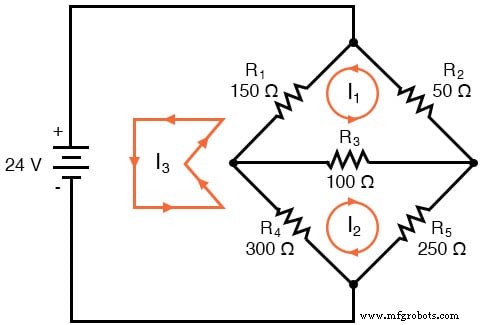
Di sini, saya telah memilih I3 untuk mengulang dari sisi bawah baterai, melalui R4 , melalui R1 , dan kembali ke sisi atas baterai. Ini bukan satu-satunya jalan yang bisa saya pilih untuk I3 , tetapi tampaknya yang paling sederhana.
Label Polaritas Penurunan Tegangan Resistor
Sekarang, kita harus memberi label pada polaritas penurunan tegangan resistor, mengikuti setiap arah arus yang diasumsikan:
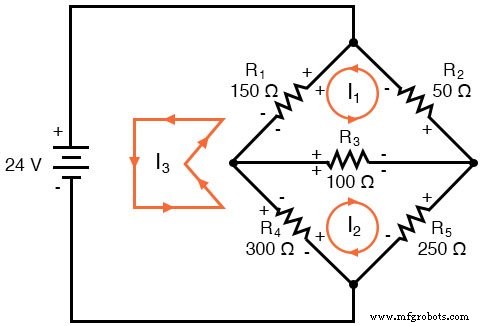
Perhatikan sesuatu yang sangat penting di sini:di resistor R4 , polaritas untuk arus mesh masing-masing tidak sesuai. Ini karena arus jala tersebut (I2 dan saya3 ) melalui R4 dalam arah yang berbeda. Ini tidak menghalangi penggunaan metode analisis Mesh Current, tetapi ini sedikit memperumitnya. Meskipun nanti, kami akan menunjukkan cara menghindari R4 bentrokan saat ini. (Lihat Contoh di bawah)
Menggunakan KVL
Menghasilkan persamaan KVL untuk loop atas jembatan, mulai dari node atas dan menelusuri searah jarum jam:

Dalam persamaan ini, kami mewakili arah umum arus dengan jumlah melalui resistor umum. Misalnya, resistor R3 , dengan nilai 100 , tegangan jatuh direpresentasikan dalam persamaan KVL di atas dengan ekspresi 100(I1 + I2 ), karena kedua arus I1 dan saya2 melalui R3 dari kanan ke kiri. Hal yang sama dapat dikatakan untuk resistor R1 , dengan ekspresi jatuh tegangan ditunjukkan sebagai 150(I1 + I3 ), karena keduanya saya1 dan saya3 pergi dari bawah ke atas melalui resistor itu, dan dengan demikian bekerja bersama untuk menghasilkan penurunan tegangan.
Menghasilkan persamaan KVL untuk loop bawah jembatan tidak akan mudah karena kita memiliki dua arus yang melawan satu sama lain melalui resistor R4 . Inilah cara saya melakukannya (mulai dari simpul kanan, dan menelusuri berlawanan arah jarum jam):

Perhatikan bagaimana suku kedua dalam bentuk asli persamaan memiliki resistor R4 nilai 300 dikalikan dengan selisih antara I2 dan saya3 (Saya2 - Saya3 ). Ini adalah bagaimana kami mewakili efek gabungan dari dua arus jala yang berlawanan arah melalui komponen yang sama. Memilih tanda matematika yang tepat sangat penting di sini:300(I2 - Saya3 ) tidak berarti sama dengan 300(I3 - Saya2 ). Saya memilih untuk menulis 300(I2 - Saya3 ) karena saya pertama-tama memikirkan I2 efek (menciptakan penurunan tegangan positif, mengukur dengan voltmeter imajiner melintasi R4 , timah merah di bawah dan timah hitam di atas), dan yang kedua dari I3 efek (menciptakan penurunan tegangan negatif, timah merah di bagian bawah dan timah hitam di bagian atas). Jika saya berpikir dalam hal I3 efek pertama dan saya2 efek kedua, memegang kabel voltmeter imajiner saya di posisi yang sama (merah di bagian bawah dan hitam di atas), ekspresinya adalah -300(I3 - Saya2 ). Perhatikan bahwa ungkapan ini adalah secara matematis setara dengan yang pertama:+300(I2 - Saya3 ).
Nah, itu menangani dua persamaan, tapi saya masih membutuhkan persamaan ketiga untuk menyelesaikan kumpulan persamaan simultan saya yang terdiri dari tiga variabel, tiga persamaan. Persamaan ketiga ini juga harus mencakup tegangan baterai, yang hingga saat ini tidak muncul di kedua persamaan KVL sebelumnya. Untuk menghasilkan persamaan ini, saya akan menelusuri loop lagi dengan voltmeter imajiner saya mulai dari terminal bawah (negatif) baterai, melangkah searah jarum jam (sekali lagi, arah langkah saya sewenang-wenang, dan tidak perlu sama dengan arah dari arus mesh dalam loop itu):

Memecahkan Arus
Memecahkan untuk I1 , saya2 , dan saya3 menggunakan metode persamaan simultan apa pun yang kami sukai:

Contoh: Gunakan Oktaf untuk menemukan solusi untuk I1 , saya2 , dan saya3 dari bentuk persamaan yang disederhanakan di atas.
Solusi: Di Octave, klon Matlab® open-source, masukkan koefisien ke dalam matriks A antara tanda kurung siku dengan elemen kolom dipisahkan koma, dan baris dipisahkan titik koma. Masukkan tegangan ke dalam vektor kolom:b. Arus yang tidak diketahui:I1 , 2 , dan saya3 dihitung dengan perintah:x=A\b. Ini terkandung dalam vektor kolom x.
oktaf:1>A =[300.100.150;100.650,-300;-150.300,-450] A =300 100 150 100 650 -300 -150 300 -450 oktaf:2> b =[0;0;-24] b =0 0 -24 oktaf:3> x =A\b x =-0,093793 0,077241 0.136092
Nilai negatif didapat untuk I1 memberitahu kita bahwa arah yang diasumsikan untuk arus mesh itu salah. Jadi, nilai arus aktual yang melalui setiap resistor adalah sebagai berikut:
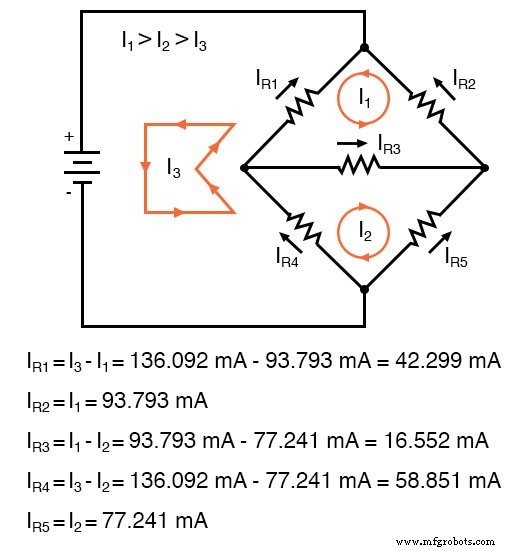
Menghitung penurunan tegangan pada setiap resistor:
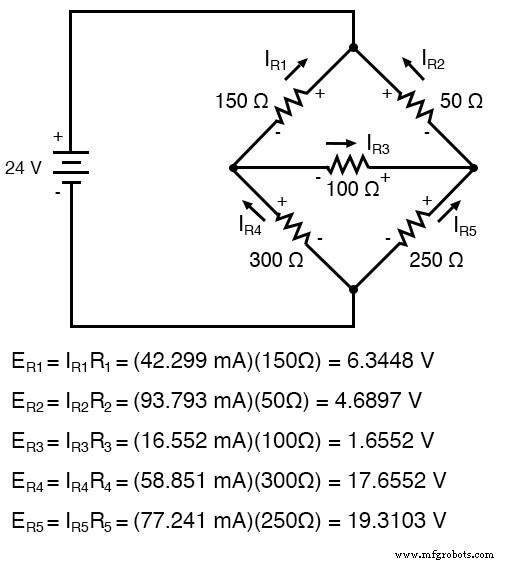
Simulasi SPICE mengkonfirmasi keakuratan perhitungan tegangan kami:
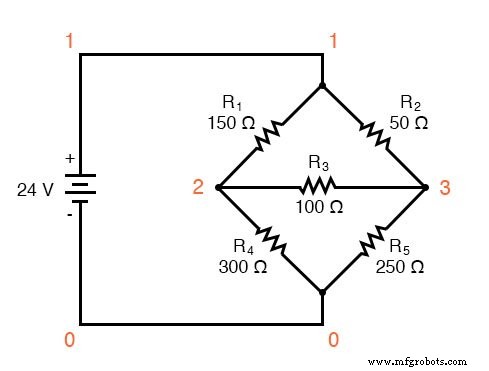
jembatan batu gandum yang tidak seimbang v1 1 0 r1 1 2 150 r2 1 3 50 r3 2 3 100 r4 2 0 300 r5 3 0 250 .dc v1 24 24 1 .cetak dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0) .akhir v1 v(1,2) v(1,3) v(3,2) v(2) v(3) 2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01
Contoh:
(a) Temukan jalur baru untuk I3 current saat ini yang tidak menghasilkan polaritas yang bertentangan pada resistor apa pun dibandingkan dengan I1 atau saya2 . R4 adalah komponen yang menyinggung. (b) Temukan nilai untuk I1 , saya2 , dan saya3 . (c) Temukan lima arus resistor dan bandingkan dengan nilai sebelumnya.
Solusi:
(a) Rute I3 melalui R5 , R3, dan R1 seperti yang ditunjukkan:
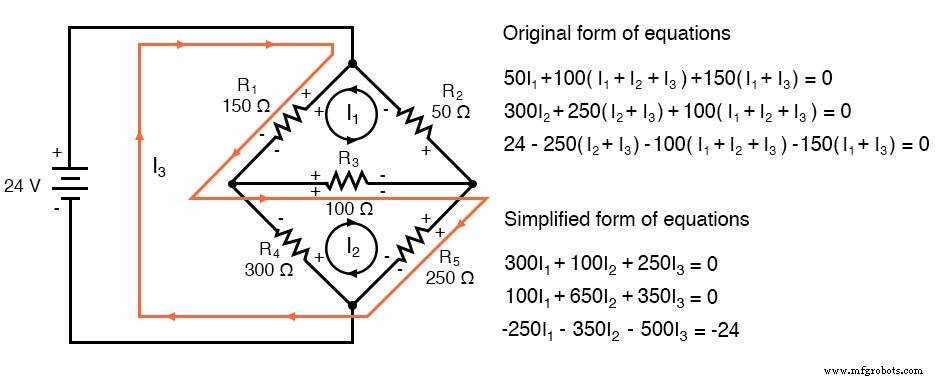
Perhatikan bahwa polaritas yang bertentangan pada R4 telah dihapus. Selain itu, tidak ada resistor lain yang memiliki polaritas yang saling bertentangan.
(b) Oktaf, klon Matlab open source (gratis), menghasilkan vektor arus mesh pada “x”:
oktaf:1> A =[300.100.250;100.650.350;-250,-350,-500] A =300 100 250 100 650 350 -250 -350 -500 oktaf:2> b =[0;0;-24] b =0 0 -24 oktaf:3> x =A\b x =-0,093793 -0,058851 0.136092
Tidak semua arus I1 , saya2 , dan saya3 adalah sama (I2 ) sebagai jembatan sebelumnya karena jalur loop yang berbeda Namun, arus resistor dibandingkan dengan nilai sebelumnya:
IR1 =I1 + I3 =-93,793 ma + 136.092 ma =42.299 ma IR2 =I1 =-93,793 ma IR3 =I1 + I2 + I3 =-93.793 ma -58.851 ma + 136.092 ma =-16.552 ma IR4 =I2 =-58,851 ma IR5 =I2 + I3 =-58.851 ma + 136.092 ma =77.241 ma
Karena arus resistor sama dengan nilai sebelumnya, tegangan resistor akan sama dan tidak perlu dihitung lagi.
TINJAUAN:
- Langkah-langkah yang harus diikuti untuk metode analisis “Mesh Current”:
- (1) Gambarkan arus mesh dalam loop sirkuit, cukup untuk memperhitungkan semua komponen.
- (2) Labeli polaritas penurunan tegangan resistor berdasarkan asumsi arah arus mesh.
- (3) Tulis persamaan KVL untuk setiap loop dari rangkaian, substitusikan produk IR untuk E di setiap suku resistor dari persamaan. Jika dua arus jala-jala berpotongan melalui suatu komponen, nyatakan arus sebagai jumlah aljabar dari kedua arus jala-jala tersebut (yaitu I1 + I2 ) jika arus mengalir dalam arah yang sama melalui komponen itu. Jika tidak, nyatakan arus pada perbedaannya (yaitu I1 - Saya2 ).
- (4) Selesaikan untuk arus mesh yang tidak diketahui (persamaan simultan).
- (5) Jika ada solusi yang negatif, maka asumsi arah arus salah!
- (6) Tambahkan arus mesh secara aljabar untuk menemukan komponen arus yang berbagi beberapa arus mesh.
- (7) Memecahkan penurunan tegangan di semua resistor (E=IR).
Arus jala dengan inspeksi
Kami melihat kedua "metode arus jala" dengan semua arus berjalan searah jarum jam (cw). Motivasinya adalah untuk menyederhanakan penulisan persamaan mesh dengan mengabaikan polaritas penurunan tegangan resistor. Padahal, kita harus memperhatikan polaritas sumber tegangan sehubungan dengan arah arus yang diasumsikan. Tanda turunnya tegangan resistor akan mengikuti pola yang tetap.
Jika kita menulis satu set persamaan arus jala konvensional untuk rangkaian di bawah ini, di mana kita memperhatikan tanda-tanda penurunan tegangan pada resistor, kita dapat mengatur ulang koefisien menjadi pola tetap:
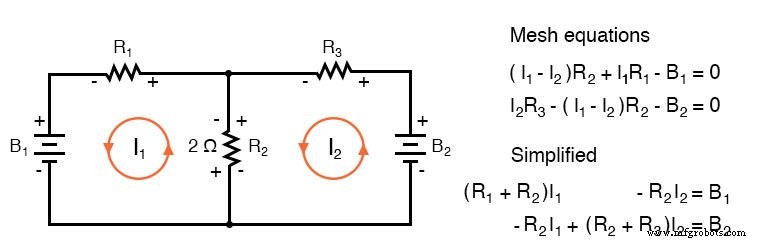
Setelah diatur ulang, kita dapat menulis persamaan dengan inspeksi. Tanda-tanda koefisien mengikuti pola tetap pada pasangan di atas atau himpunan tiga dalam aturan di bawah.
Aturan jala saat ini:
- Metode ini mengasumsikan sumber tegangan aliran arus konvensional. Ganti sumber arus apa pun secara paralel dengan resistor dengan sumber tegangan setara yang dirangkai secara seri dengan resistansi setara.
- Mengabaikan arah arus atau polaritas tegangan pada resistor, menggambar loop arus berlawanan arah jarum jam yang melintasi semua komponen. Hindari pengulangan bersarang.
- Tulis persamaan hukum tegangan dalam bentuk arus yang tidak diketahui:I1 , saya2 , dan saya3 . Koefisien persamaan 1, persamaan 2, koefisien 2, dan koefisien persamaan 3 adalah jumlah positif dari resistor di sekitar loop masing-masing.
- Semua koefisien lainnya negatif, mewakili resistansi yang umum untuk sepasang loop. Persamaan 1 koefisien 2 adalah resistor yang umum untuk loop 1 dan 2, koefisien 3 resistor yang umum untuk loop 1 dan 3. Ulangi untuk persamaan dan koefisien lainnya.
- +(jumlah loop R 1)I1 - (loop R umum 1-2)I2 - (loop R umum 1-3)I3 =E1
-(loop R umum 1-2)I1 + ( jumlah loop R 2)I2 - (loop R umum 2-3)I3 =E2
-(loop R umum 1-3)I1 - (loop R umum 2-3)I2 + (jumlah loop R 3 )I3 =E3
- Sisi kanan persamaan sama dengan sumber tegangan aliran arus elektron. Kenaikan tegangan sehubungan dengan arus yang diasumsikan berlawanan arah jarum jam adalah positif, dan 0 untuk tanpa sumber tegangan.
- Pecahkan persamaan untuk arus jala:I1 , saya2 , dan I3. Memecahkan arus melalui resistor individu dengan KCL. Selesaikan voltase dengan Hukum Ohm dan KVL.
Sementara aturan di atas khusus untuk sirkuit tiga mesh, aturan dapat diperluas ke mesh yang lebih kecil atau lebih besar. Gambar di bawah mengilustrasikan penerapan aturan. Ketiga arus ditarik ke arah yang sama, searah jarum jam. Satu persamaan KVL ditulis untuk masing-masing dari tiga loop. Perhatikan bahwa tidak ada polaritas yang ditarik pada resistor. Kami tidak membutuhkannya untuk menentukan tanda-tanda koefisien. Padahal kita perlu memperhatikan polaritas sumber tegangan terhadap arah arus. I3 arus searah jarum jam mengalir keluar dari terminal positif (+) sumber l24V kemudian kembali ke terminal (-). Ini adalah kenaikan tegangan untuk aliran arus konvensional. Oleh karena itu, persamaan ketiga ruas kanan adalah -24V.
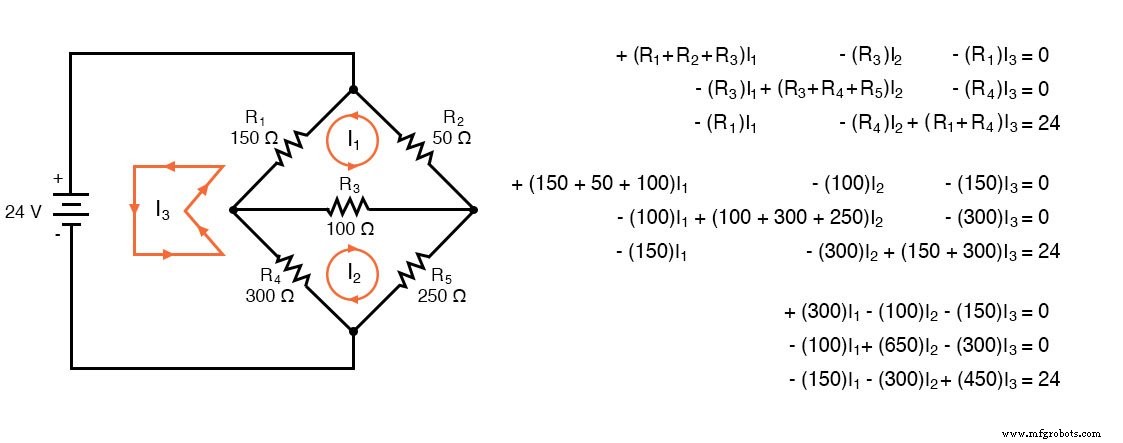
Dalam Oktaf, masukkan koefisien ke dalam matriks A dengan elemen kolom dipisahkan koma, dan baris dipisahkan titik koma. Masukkan tegangan ke dalam vektor kolom b. Selesaikan untuk arus yang tidak diketahui:I1 , saya2 , dan saya3 dengan perintah:x=A\b. Arus ini terkandung dalam vektor kolom x. Nilai positif menunjukkan bahwa ketiga arus mesh semuanya mengalir searah jarum jam yang diasumsikan.
oktaf:2> A=[300,-100,-150;-100,650,-300;-150,-300,450] A =300 -100 -150 -100 650 -300 -150 -300 450 oktaf:3> b=[0;0;24] b =0 0 24 oktaf:4> x=A\b x =0,093793 0,077241 0.136092
Arus mesh cocok dengan solusi sebelumnya dengan metode arus mesh yang berbeda. Perhitungan tegangan dan arus resistor akan identik dengan solusi sebelumnya. Tidak perlu mengulang di sini.
Perhatikan bahwa teks teknik elektro didasarkan pada aliran arus konvensional. Metode loop-current, mesh-current dalam teks tersebut akan menjalankan asumsi arus mesh searah jarum jam . Arus konvensional mengalir keluar terminal (+) baterai melalui sirkuit, kembali ke terminal (-). Kenaikan tegangan arus konvensional sesuai dengan penelusuran arus yang diasumsikan dari (-) ke (+) melalui sumber tegangan apa pun.
Satu lagi contoh rangkaian sebelumnya berikut ini. Resistansi di sekitar loop 1 adalah 6 , di sekitar loop 2:3 . Resistansi umum untuk kedua loop adalah 2 . Perhatikan koefisien dari I1 dan saya2 dalam pasangan persamaan. Menelusuri arus loop 1 searah jarum jam yang diasumsikan melalui B1 dari (+) ke (-) sesuai dengan kenaikan tegangan aliran arus elektron.
Jadi, tanda dari 28 V adalah positif. Loop 2 berlawanan arah jarum jam mengasumsikan jejak arus (-) ke (+) melalui B2 , penurunan tegangan. Jadi, tanda B2 negatif, -7 dalam persamaan mesh ke-2. Sekali lagi, tidak ada tanda polaritas pada resistor. Mereka juga tidak menemukan persamaan.
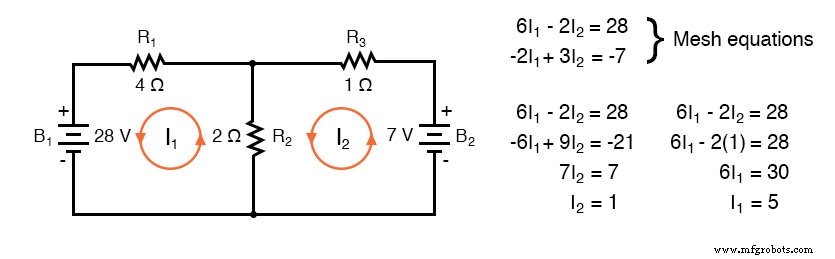
Arus I1 =5 A, dan I2 =1 A keduanya positif. Keduanya mengalir searah jarum jam. Ini dibandingkan dengan hasil sebelumnya.
Ringkasan:
- Metode arus jala yang dimodifikasi menghindari keharusan untuk menentukan tanda-tanda koefisien persamaan dengan menggambar semua arus jala searah jarum jam untuk aliran arus konvensional.
- Namun, kita perlu menentukan tanda sumber tegangan apa pun dalam loop. Sumber tegangan positif jika diasumsikan arus ccw mengalir bersama baterai (sumber). Tandanya negatif jika diasumsikan arus ccw mengalir melawan baterai.
- Lihat aturan di atas untuk detailnya.
LEMBAR KERJA TERKAIT:
- Lembar Kerja Analisis Arus DC Mesh