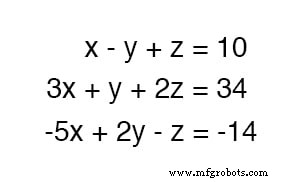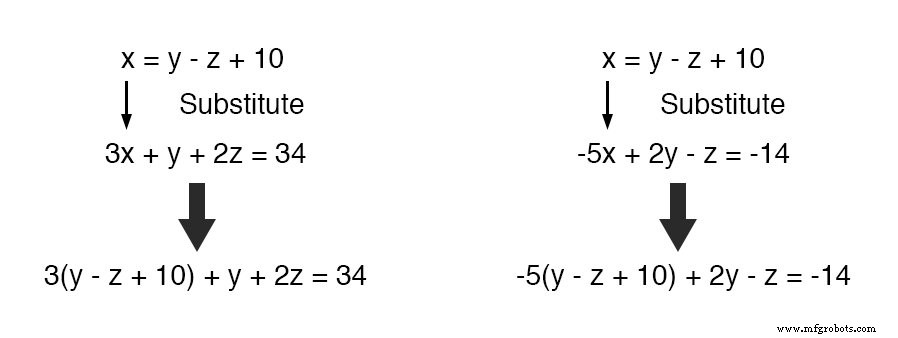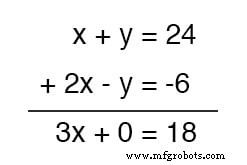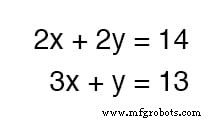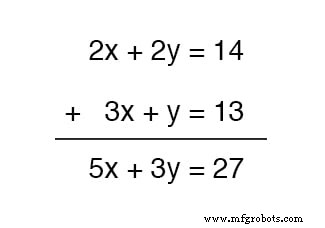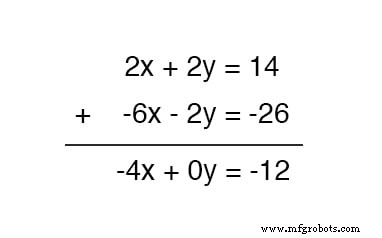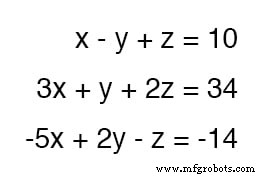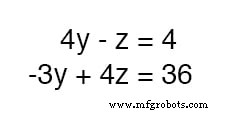Menyelesaikan Persamaan Simultan:Metode Substitusi dan Metode Penambahan

Apakah Persamaan dan Sistem Persamaan Simultan itu?

Istilah persamaan simultan dan sistem persamaan merujuk pada kondisi di mana dua atau lebih variabel yang tidak diketahui terkait satu sama lain melalui jumlah persamaan yang sama.

Contoh:

Untuk himpunan persamaan ini, hanya ada satu kombinasi nilai untuk x dan y yang akan memuaskan keduanya.

Persamaan mana pun, yang dipertimbangkan secara terpisah, memiliki tak terhingga dari (x,y) . yang valid solusi, tapi bersama hanya ada satu. Diplot pada grafik, kondisi ini menjadi jelas:

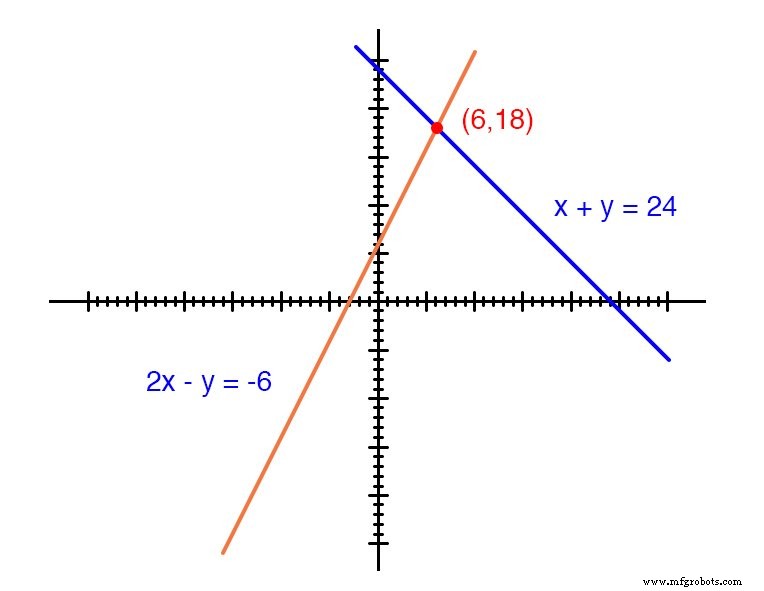
Setiap garis sebenarnya merupakan rangkaian titik yang mewakili kemungkinan x dan y pasangan solusi untuk setiap persamaan.

Setiap persamaan, secara terpisah, memiliki jumlah pasangan terurut yang tak terhingga (x ,y ) solusi. Hanya ada satu titik dimana kedua fungsi linier x + y =24 dan 2x - y =-6 berpotongan (di mana salah satu dari banyak solusi independen mereka bekerja untuk kedua persamaan), dan di sanalah x sama dengan nilai 6 dan y sama dengan nilai 18.

Namun, biasanya, grafik bukanlah cara yang sangat efisien untuk menentukan himpunan solusi simultan untuk dua atau lebih persamaan. Ini sangat tidak praktis untuk sistem dengan tiga variabel atau lebih.

Dalam sistem tiga variabel, misalnya, solusinya akan ditemukan dengan titik potong tiga bidang dalam ruang koordinat tiga dimensi—bukan skenario yang mudah untuk divisualisasikan.

Menyelesaikan Persamaan Simultan Menggunakan Metode Substitusi

Ada beberapa teknik aljabar untuk menyelesaikan persamaan simultan.

Mungkin yang paling mudah dipahami adalah substitusi metode.

Ambil, misalnya, masalah contoh dua variabel kami:

Dalam metode substitusi, kita memanipulasi salah satu persamaan sedemikian rupa sehingga satu variabel didefinisikan dalam istilah yang lain:

Kemudian, kita ambil definisi baru ini dari satu variabel dan pengganti untuk variabel yang sama dalam persamaan lainnya.

Dalam hal ini, kami mengambil definisi y , yaitu 24 - x dan gantikan ini dengan y istilah yang ditemukan dalam persamaan lain:

Sekarang kita memiliki persamaan hanya dengan satu variabel (x ), kita dapat menyelesaikannya menggunakan teknik aljabar “normal”:

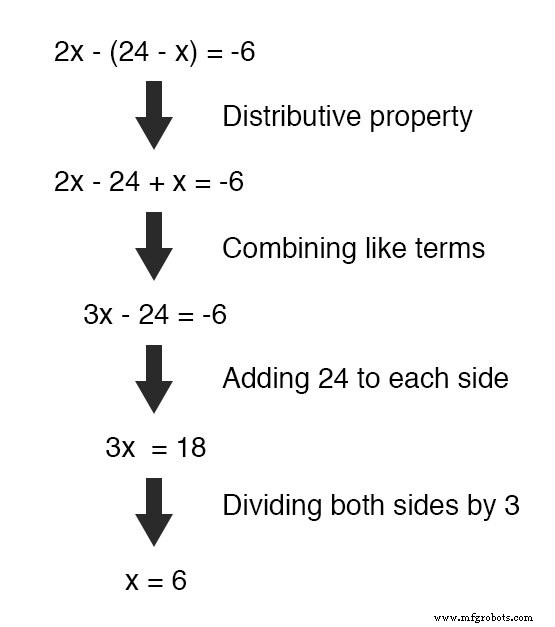
Sekarang x diketahui, kita dapat memasukkan nilai ini ke salah satu persamaan asli dan mendapatkan nilai untuk y.

Atau, untuk menghemat beberapa pekerjaan, kita dapat memasukkan nilai ini (6) ke dalam persamaan yang baru saja kita buat untuk mendefinisikan y dalam hal x , karena sudah dalam bentuk untuk dipecahkan y :

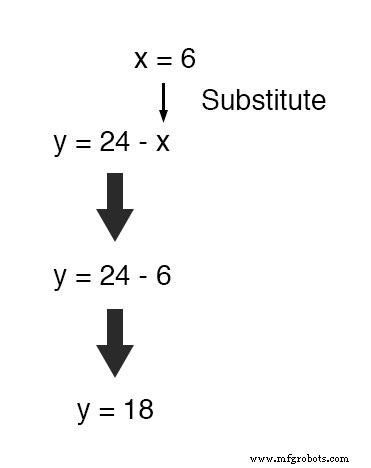
Menerapkan metode substitusi ke sistem tiga atau lebih variabel melibatkan pola yang sama, hanya dengan lebih banyak pekerjaan yang terlibat.

Hal ini umumnya berlaku untuk metode solusi apa pun:jumlah langkah yang diperlukan untuk mendapatkan solusi meningkat pesat dengan setiap variabel tambahan dalam sistem.

Untuk menyelesaikan tiga variabel yang tidak diketahui, kita membutuhkan setidaknya tiga persamaan. Perhatikan contoh ini:

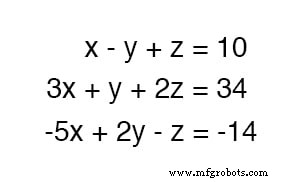
Karena persamaan pertama memiliki koefisien paling sederhana (1, -1, dan 1, untuk x , y , dan z , masing-masing), tampaknya logis untuk menggunakannya untuk mengembangkan definisi satu variabel dalam kaitannya dengan dua variabel lainnya.

Selesaikan untuk x dalam hal y dan z :

Sekarang, kita dapat mengganti definisi x dimana x muncul dalam dua persamaan lainnya:

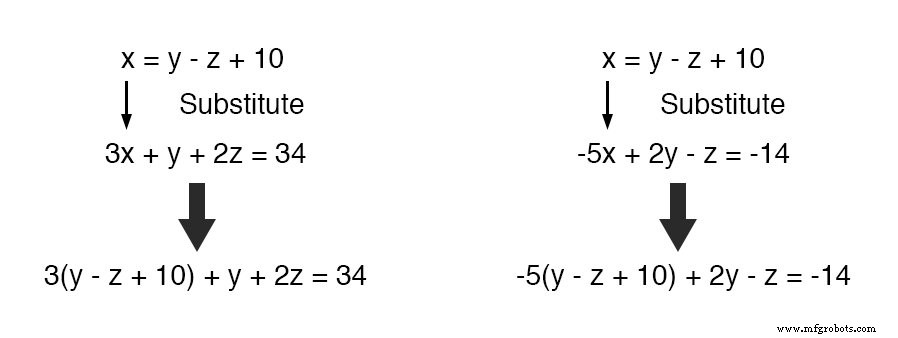
Reduksi kedua persamaan ini menjadi bentuk yang paling sederhana:

Sejauh ini, upaya kami telah mereduksi sistem dari tiga variabel dalam tiga persamaan menjadi dua variabel dalam dua persamaan.

Sekarang, kita bisa menerapkan teknik substitusi lagi pada kedua persamaan 4y - z =4 dan -3y + 4z =36 untuk memecahkan salah satu y atau z . Pertama, saya akan memanipulasi persamaan pertama untuk mendefinisikan z dalam hal y :

Selanjutnya, kita akan mengganti definisi z dalam hal y di mana kita melihat z dalam persamaan lain:

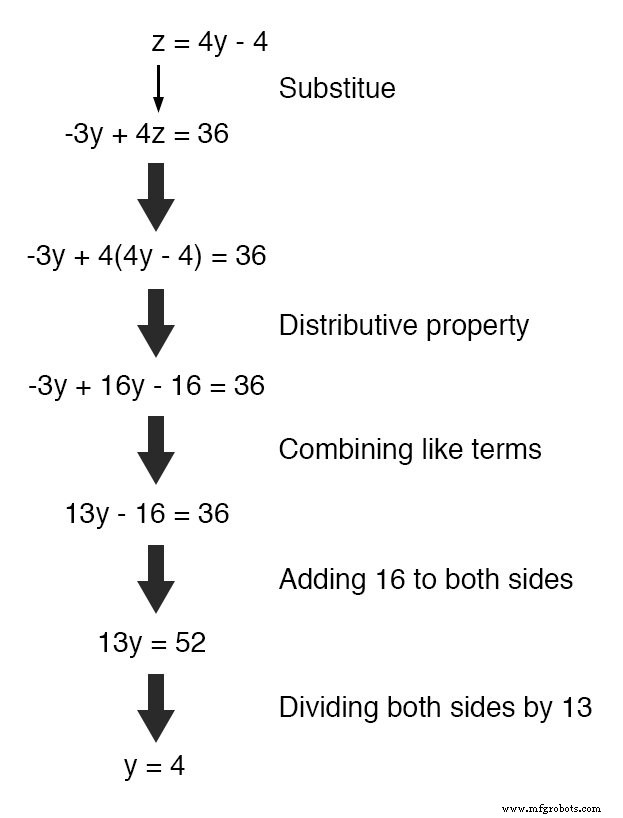
Sekarang y adalah nilai yang diketahui, kita dapat memasukkannya ke dalam persamaan yang mendefinisikan z dalam hal y dan dapatkan angka untuk z :

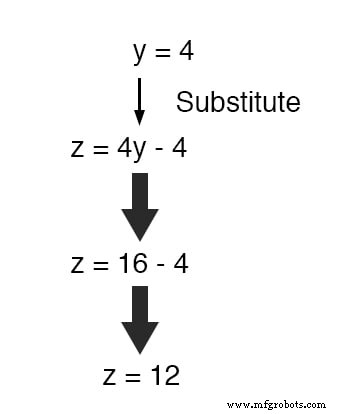
Sekarang, dengan nilai untuk y dan z diketahui, kita dapat memasukkan ini ke dalam persamaan di mana kita mendefinisikan x dalam hal y dan z , untuk mendapatkan nilai x :

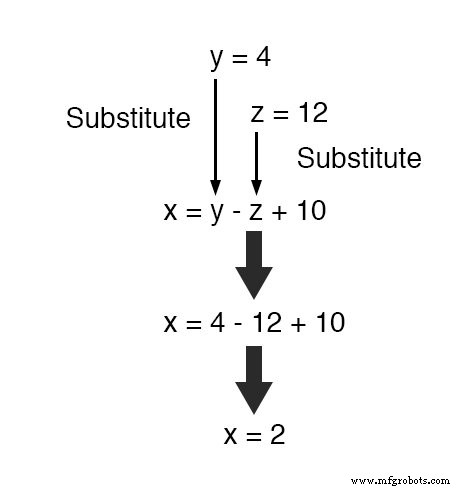
Sebagai penutup, kami menemukan nilai untuk x , y , dan z dari 2, 4, dan 12, masing-masing, yang memenuhi ketiga persamaan.

Menyelesaikan Persamaan Simultan Menggunakan Metode Penjumlahan

Meskipun metode substitusi mungkin yang paling mudah dipahami pada tingkat konseptual, ada metode solusi lain yang tersedia bagi kita.

Salah satu metode tersebut adalah apa yang disebut penambahan metode, di mana persamaan ditambahkan satu sama lain untuk tujuan menghilangkan suku-suku variabel.

Mari kita ambil sistem dua variabel yang digunakan untuk mendemonstrasikan metode substitusi:

Salah satu aturan aljabar yang paling sering digunakan adalah Anda dapat melakukan operasi aritmatika apa pun yang Anda inginkan untuk persamaan selama Anda melakukannya sama ke kedua sisi .

Dengan mengacu pada penambahan, ini berarti kita dapat menambahkan kuantitas apa pun yang kita inginkan ke kedua sisi persamaan—asalkan sama kuantitas—tanpa mengubah kebenaran persamaan.

Pilihan yang kita miliki adalah menjumlahkan sisi persamaan yang bersesuaian untuk membentuk persamaan baru.

Karena setiap persamaan adalah ekspresi kesetaraan (jumlah yang sama di kedua sisi = tanda), menambahkan ruas kiri satu persamaan ke ruas kiri persamaan lainnya adalah valid selama kita menambahkan ruas kanan kedua persamaan itu bersama-sama.

Dalam contoh himpunan persamaan kita, misalnya, kita dapat menambahkan x + y untuk 2x - y , dan tambahkan 24 dan -6 bersama-sama juga untuk membentuk persamaan baru.

Apa manfaatnya bagi kita? Periksa apa yang terjadi ketika kita melakukan ini pada kumpulan persamaan contoh kita:

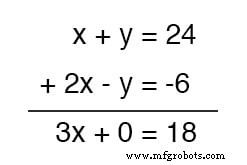
Karena persamaan teratas kebetulan mengandung y positive positif istilah sedangkan persamaan bawah kebetulan mengandung y negative negatif istilah, kedua istilah ini saling membatalkan dalam proses penambahan, tanpa meninggalkan y istilah dalam jumlah.

Yang tersisa adalah persamaan baru, tetapi persamaan dengan hanya satu variabel yang tidak diketahui, x ! Ini memungkinkan kita untuk dengan mudah memecahkan nilai x :

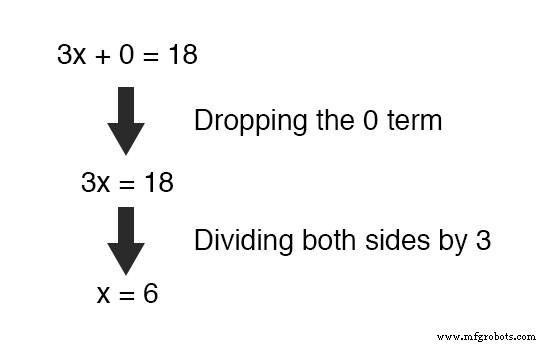
Setelah kita memiliki nilai yang diketahui untuk x , tentu saja, menentukan y nilai hanyalah masalah substitusi (menggantikan x dengan nomor 6 ) menjadi salah satu persamaan asli.

Dalam contoh ini, teknik penjumlahan persamaan bekerja dengan baik untuk menghasilkan persamaan dengan variabel tunggal yang tidak diketahui.

Bagaimana dengan contoh di mana hal-hal tidak begitu sederhana? Perhatikan himpunan persamaan berikut:

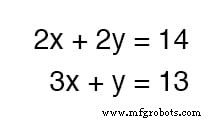
Kita dapat menjumlahkan kedua persamaan ini—ini adalah operasi aljabar yang benar-benar valid—tetapi ini tidak akan menguntungkan kita dalam tujuan memperoleh nilai untuk x dan y :

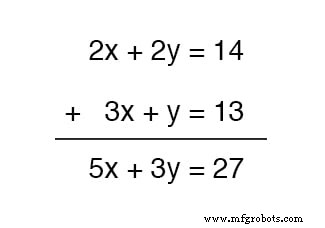
Persamaan yang dihasilkan masih berisi dua variabel yang tidak diketahui, sama seperti persamaan aslinya, sehingga kita tidak perlu lagi mencari solusi.

Namun, bagaimana jika kita dapat memanipulasi salah satu persamaan sehingga memiliki suku negatif yang akan batalkan suku masing-masing dalam persamaan lain saat ditambahkan?

Kemudian, sistem akan direduksi menjadi persamaan tunggal dengan variabel tunggal yang tidak diketahui seperti contoh terakhir (kebetulan).

Jika kita hanya bisa memutar y suku dalam persamaan bawah menjadi - 2y suku, sehingga ketika kedua persamaan dijumlahkan, keduanya y istilah dalam persamaan akan dibatalkan, hanya menyisakan x istilah, ini akan membawa kita lebih dekat ke solusi.

Untungnya, ini tidak sulit untuk dilakukan. Jika kita menggandakan setiap suku dari persamaan yang lebih rendah dengan -2 , itu akan menghasilkan hasil yang kita cari:

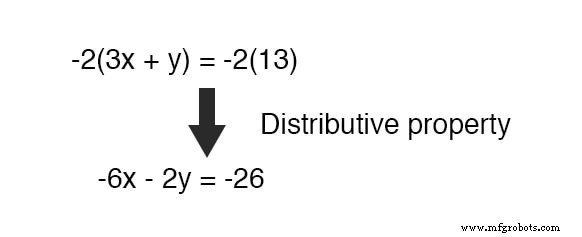
Sekarang, kita dapat menambahkan persamaan baru ini ke persamaan atas yang asli:

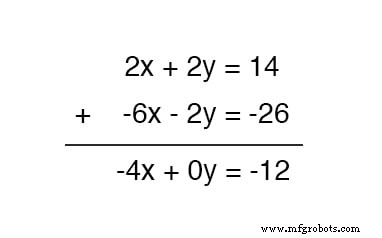
Memecahkan x , kita memperoleh nilai 3 :

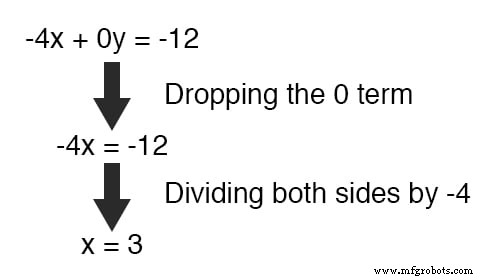
Mengganti nilai yang baru ditemukan ini untuk x ke dalam salah satu persamaan asli, nilai y mudah ditentukan:

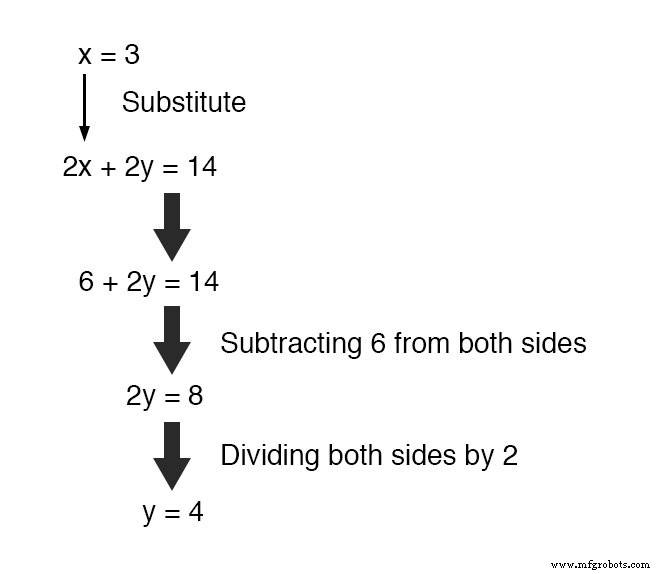
Menggunakan teknik solusi ini pada sistem tiga variabel sedikit lebih rumit.

Seperti halnya substitusi, Anda harus menggunakan teknik ini untuk mereduksi sistem tiga persamaan tiga variabel menjadi dua persamaan dengan dua variabel, lalu menerapkannya kembali untuk mendapatkan satu persamaan dengan satu variabel yang tidak diketahui.

Untuk mendemonstrasikannya, saya akan menggunakan sistem persamaan tiga variabel dari bagian substitusi:

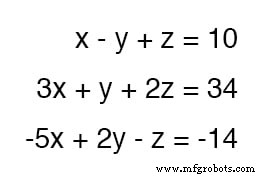
Karena persamaan teratas memiliki nilai koefisien 1 untuk setiap variabel, ini akan menjadi persamaan yang mudah untuk dimanipulasi dan digunakan sebagai alat pembatalan.

Misalnya, jika kita ingin membatalkan 3x suku dari persamaan tengah, yang perlu kita lakukan adalah mengambil persamaan teratas, kalikan setiap sukunya dengan -3 , lalu tambahkan ke persamaan tengah seperti ini:

Kita dapat menghilangkan persamaan bawah dari -5x suku dengan cara yang sama:ambil persamaan teratas asli, kalikan setiap sukunya dengan 5 , lalu tambahkan persamaan yang dimodifikasi ke persamaan bawah, meninggalkan persamaan baru dengan hanya y dan z syarat:

Pada titik ini, kita memiliki dua persamaan dengan dua variabel yang tidak diketahui sama, y dan z :

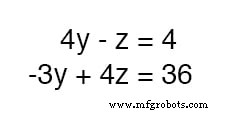
Dengan inspeksi, harus terbukti bahwa -z istilah persamaan atas dapat dimanfaatkan untuk membatalkan 4z suku dalam persamaan bawah hanya jika kita mengalikan setiap suku pada persamaan atas dengan 4 dan jumlahkan kedua persamaan menjadi satu:

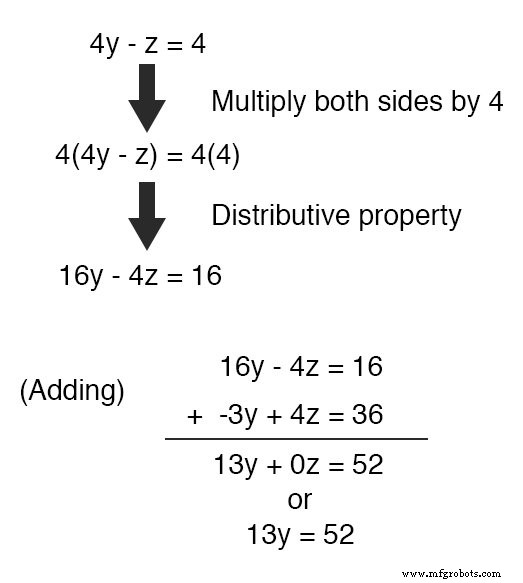
Mengambil persamaan baru 13y =52 dan penyelesaian untuk y (dengan membagi kedua ruas dengan 13 ), kita mendapatkan nilai 4 untuk y .

Mengganti nilai 4 . ini untuk y dalam salah satu dari persamaan dua variabel memungkinkan kita untuk memecahkan z .

Substitusikan kedua nilai y dan z ke salah satu dari persamaan tiga variabel asli memungkinkan kita untuk memecahkan x .

Hasil akhirnya (saya akan memberikan Anda langkah-langkah aljabar karena Anda seharusnya sudah mengetahuinya sekarang!) adalah x =2 , y =4 , dan z =12 .

LEMBAR KERJA TERKAIT:

• Persamaan Simultan untuk Lembar Kerja Analisis Sirkuit