Aritmatika Bilangan Kompleks

Karena bilangan kompleks adalah entitas matematika yang sah, seperti halnya bilangan skalar, bilangan tersebut dapat ditambahkan, dikurangkan, dikalikan, dibagi, dikuadratkan, dibalik, dan semacamnya, sama seperti jenis bilangan lainnya.

Beberapa kalkulator ilmiah diprogram untuk melakukan operasi ini secara langsung pada dua atau lebih bilangan kompleks, tetapi operasi ini juga dapat dilakukan "dengan tangan". Bagian ini akan menunjukkan kepada Anda bagaimana operasi dasar dilakukan.

Ini sangat direkomendasikan agar Anda melengkapi diri Anda dengan kalkulator ilmiah yang mampu melakukan fungsi aritmatika dengan mudah pada bilangan kompleks. Ini akan membuat studi Anda tentang sirkuit AC jauh lebih menyenangkan daripada jika Anda dipaksa untuk melakukan semua perhitungan dengan cara yang lebih lama.

Penjumlahan dan Pengurangan Bilangan Kompleks Bentuk Persegi Panjang

Penjumlahan dan pengurangan bilangan kompleks dalam bentuk persegi panjang itu mudah. Untuk penjumlahan, cukup menjumlahkan komponen real dari bilangan kompleks untuk menentukan komponen real dari jumlah, dan menjumlahkan komponen imajiner dari bilangan kompleks untuk menentukan komponen imajiner dari jumlah:

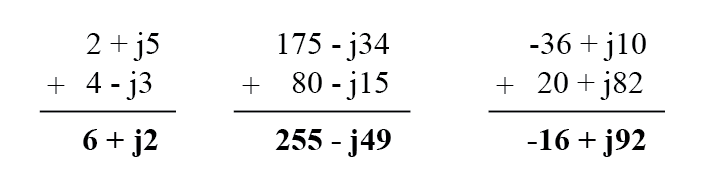
Saat mengurangkan bilangan kompleks dalam bentuk persegi panjang, cukup kurangi komponen real dari bilangan kompleks kedua dari komponen nyata dari yang pertama untuk sampai pada komponen nyata dari perbedaan, dan kurangi komponen imajiner dari bilangan kompleks kedua dari komponen imajiner dari yang pertama tiba komponen imajiner dari perbedaan:

Perkalian dan Pembagian Bilangan Kompleks dalam Bentuk Kutub

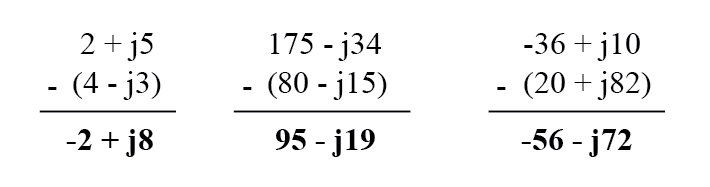
Untuk perkalian dan pembagian dengan tangan, polar adalah notasi yang disukai untuk digunakan. Saat mengalikan bilangan kompleks dalam bentuk polar, cukup kalikan besaran kutub bilangan kompleks untuk menentukan besaran kutub produk, dan tambahkan sudut bilangan kompleks untuk menentukan sudut perkalian:

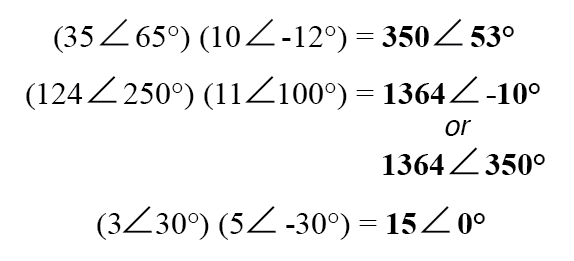
Pembagian bilangan kompleks bentuk kutub juga mudah:cukup bagi besaran kutub dari bilangan kompleks pertama dengan besaran kutub dari bilangan kompleks kedua untuk sampai pada besaran kutub hasil bagi, dan kurangi sudut bilangan kompleks kedua dari sudut bilangan kompleks pertama yang sampai pada sudut hasil bagi:

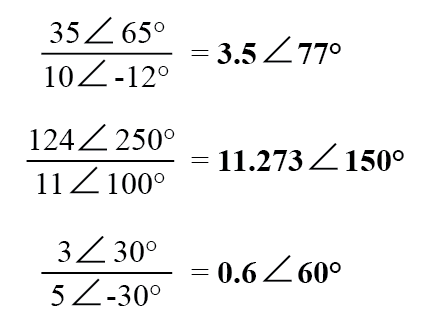
Untuk memperoleh kebalikan, atau “membalik” (1/x), bilangan kompleks, cukup bagi bilangan tersebut (dalam bentuk kutub) menjadi nilai skalar 1, yang tidak lebih dari bilangan kompleks tanpa komponen imajiner (sudut =0):

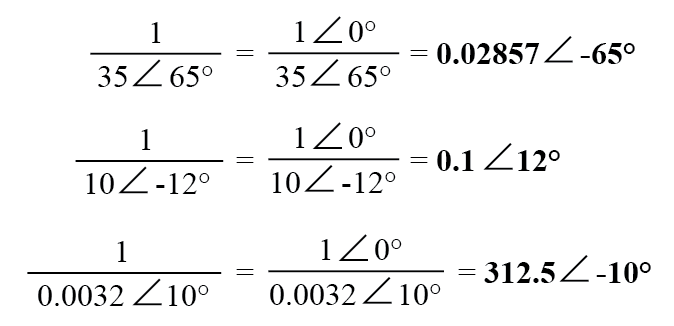
Ini adalah operasi dasar yang perlu Anda ketahui untuk memanipulasi bilangan kompleks dalam analisis rangkaian AC. Namun, operasi dengan bilangan kompleks tidak terbatas hanya pada penjumlahan, pengurangan, perkalian, pembagian, dan inversi.

Hampir semua operasi aritmatika yang dapat dilakukan dengan bilangan skalar dapat dilakukan dengan bilangan kompleks, termasuk pangkat, akar, penyelesaian persamaan simultan dengan koefisien kompleks, dan bahkan fungsi trigonometri (walaupun ini melibatkan perspektif baru dalam trigonometri yang disebut fungsi hiperbolik yang jauh di luar cakupan diskusi ini).

Pastikan Anda terbiasa dengan operasi aritmatika dasar penjumlahan, pengurangan, perkalian, pembagian, dan inversi, dan Anda tidak akan kesulitan dengan analisis rangkaian AC.

TINJAUAN:

• Untuk menjumlahkan bilangan kompleks dalam bentuk persegi panjang, tambahkan komponen real dan tambahkan komponen imajiner. Pengurangan serupa.
• Untuk mengalikan bilangan kompleks dalam bentuk kutub, kalikan besaran dan jumlahkan sudutnya. Untuk membagi, bagilah besaran dan kurangi satu sudut dari sudut lainnya.

LEMBAR KERJA TERKAIT:

• Lembar Kerja fase AC