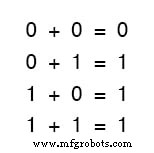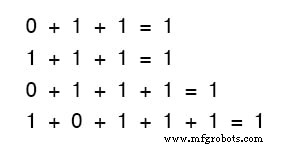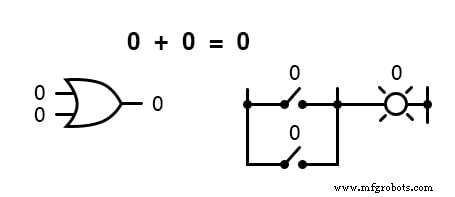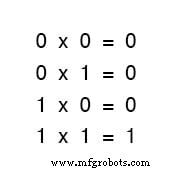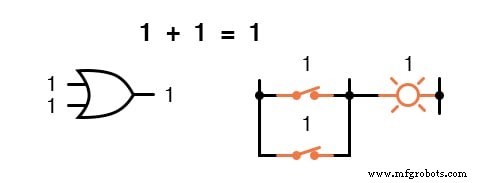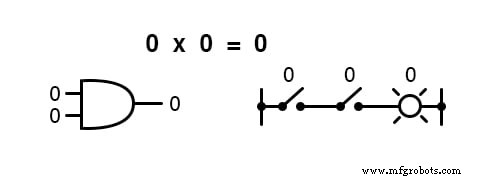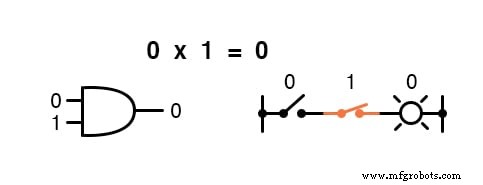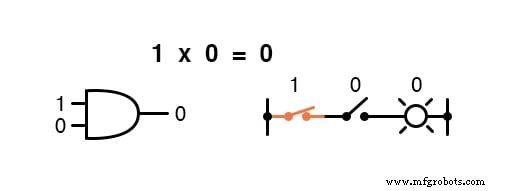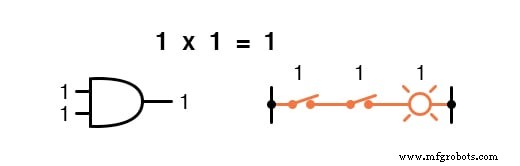Aritmatika Boolean

Mari kita mulai eksplorasi aljabar Boolean kita dengan menjumlahkan bilangan:

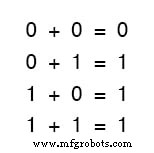
Tiga penjumlahan pertama sangat masuk akal bagi siapa pun yang akrab dengan penjumlahan dasar.

Jumlah terakhir, bagaimanapun, sangat mungkin bertanggung jawab atas lebih banyak kebingungan daripada pernyataan tunggal lainnya dalam elektronik digital, karena tampaknya bertentangan dengan prinsip-prinsip dasar matematika.

Ya, itu bertentangan dengan prinsip penjumlahan untuk bilangan real, tetapi tidak untuk bilangan Boolean.

Ingatlah bahwa dalam dunia aljabar Boolean, hanya ada dua nilai yang mungkin untuk besaran apa pun dan untuk operasi aritmatika apa pun:1 atau 0.

Tidak ada yang namanya "2" dalam lingkup nilai Boolean. Karena jumlah “1 + 1” pasti bukan 0, itu pasti 1 dengan proses eliminasi.

Tidak masalah berapa banyak atau sedikit istilah yang kita tambahkan bersama. Pertimbangkan jumlah berikut:

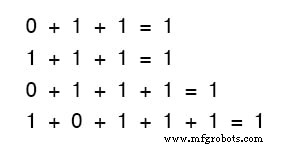
Gerbang ATAU

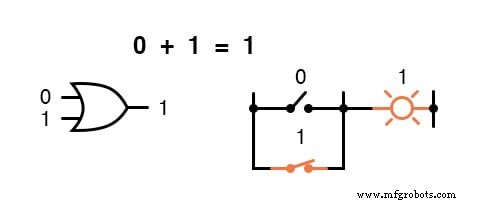
Perhatikan baik-baik jumlah dua suku pada himpunan persamaan pertama.

Apakah pola itu terlihat familier bagi Anda? Itu harus! Ini adalah pola yang sama dari 1 dan 0 seperti yang terlihat pada tabel kebenaran untuk gerbang OR.

Dengan kata lain, penambahan Boolean sesuai dengan fungsi logis dari gerbang “ATAU”, serta kontak sakelar paralel:

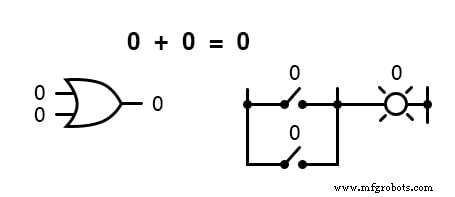
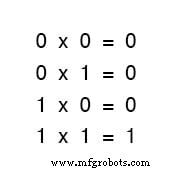
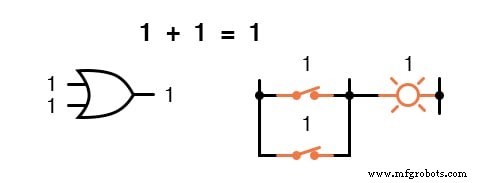
Tidak ada pengurangan dalam bidang matematika Boolean.

Pengurangan menyiratkan adanya bilangan negatif:5 - 3 adalah hal yang sama dengan 5 + (-3) , dan dalam aljabar Boolean kuantitas negatif dilarang.

Tidak ada yang namanya pembagian dalam matematika Boolean, karena pembagian sebenarnya tidak lebih dari pengurangan gabungan , dengan cara yang sama seperti perkalian penjumlahan majemuk .

Gerbang DAN

Perkalian valid dalam aljabar Boolean, dan untungnya itu sama dengan aljabar bilangan real:apa pun dikalikan dengan 0 adalah 0 , dan apa pun dikalikan dengan 1 tetap tidak berubah:

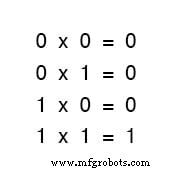
Himpunan persamaan ini juga akan terlihat familier bagi Anda:ini adalah pola yang sama yang ditemukan dalam tabel kebenaran untuk gerbang AND.

Dengan kata lain, perkalian Boolean sesuai dengan fungsi logika dari “DAN gerbang ”, serta ke kontak sakelar seri:

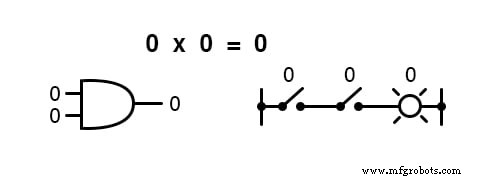
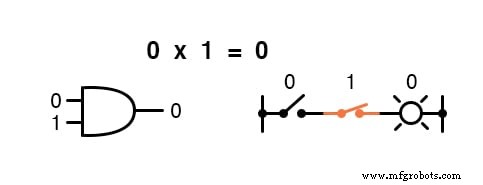
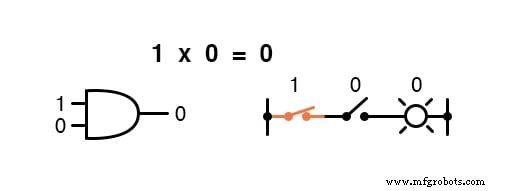
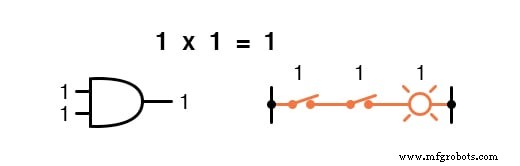
Seperti aljabar “normal”, aljabar Boolean menggunakan huruf alfabet untuk menunjukkan variabel.

Namun, tidak seperti aljabar “normal”, variabel Boolean selalu berupa huruf KAPITAL, tidak pernah menggunakan huruf kecil.

Karena mereka hanya diperbolehkan memiliki satu dari dua kemungkinan nilai, baik 1 atau 0 , setiap variabel memiliki pelengkap :kebalikan dari nilainya.

Misalnya, jika variabel “A ” memiliki nilai 0 , maka komplemen dari A memiliki nilai 1 .

Notasi Boolean menggunakan bilah di atas karakter variabel untuk menunjukkan komplemen, seperti ini:

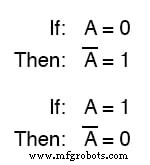
BUKAN Gerbang

Dalam bentuk tertulis, pelengkap dari “A ” dilambangkan sebagai “T-tidak ” atau “Bilah-A ”. Terkadang simbol “prima” digunakan untuk mewakili pelengkap.

Misalnya, A ' akan menjadi pelengkap dari A , sama seperti menggunakan simbol prima untuk menunjukkan diferensiasi dalam kalkulus daripada notasi pecahan d/dt .

Namun, biasanya simbol "bar" lebih banyak digunakan daripada "utama ”, untuk alasan yang akan menjadi lebih jelas nanti di bab ini.

Komplementasi Boolean menemukan kesetaraan dalam bentuk gerbang NOT , atau sakelar atau kontak relai yang biasanya tertutup:

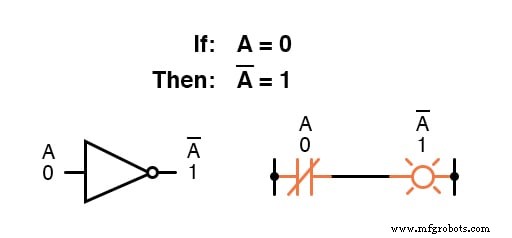
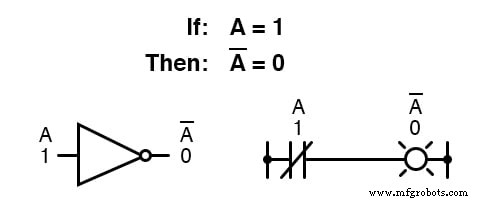
Definisi dasar besaran Boolean telah mengarah pada aturan sederhana penjumlahan dan perkalian, dan telah mengecualikan pengurangan dan pembagian sebagai operasi aritmatika yang valid.

Kami memiliki simbologi untuk menunjukkan variabel Boolean, dan pelengkapnya. Di bagian selanjutnya kita akan melanjutkan untuk mengembangkan identitas Boolean.

TINJAUAN:

• Penjumlahan Boolean setara dengan ATAU fungsi logika, serta kontak sakelar paralel.
• Perkalian Boolean setara dengan DAN fungsi logika, serta kontak sakelar seri.
• Komplementasi Boolean setara dengan NOT fungsi logika, serta tertutup secara normal menyampaikan kontak.

LEMBAR KERJA TERKAIT:

• Lembar Kerja Aljabar Boolean