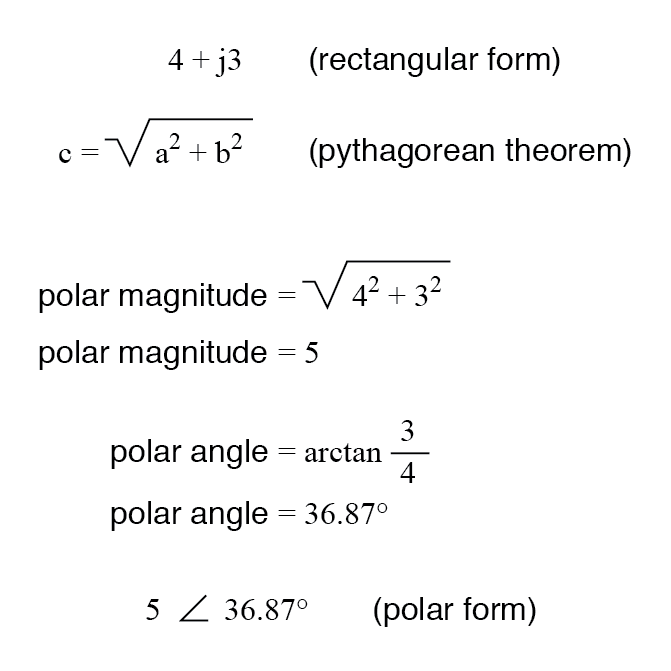Notasi Bentuk Kutub dan Bentuk Persegi Panjang untuk Bilangan Kompleks
Untuk bekerja dengan bilangan kompleks tanpa menggambar vektor, pertama-tama kita membutuhkan semacam notasi matematika standar. Ada dua bentuk dasar dari notasi bilangan kompleks:polar dan persegi panjang .
Bentuk Kutub dari Bilangan Kompleks
Bentuk kutub adalah di mana bilangan kompleks dilambangkan dengan panjang (atau dikenal sebagai magnitudo , nilai mutlak , atau modulus ) dan sudut dari vektornya (biasanya dilambangkan dengan simbol sudut yang terlihat seperti ini:).
Untuk menggunakan analogi peta, notasi kutub untuk vektor dari New York City ke San Diego akan menjadi seperti “2400 mil, barat daya.” Berikut adalah dua contoh vektor dan notasi kutubnya:
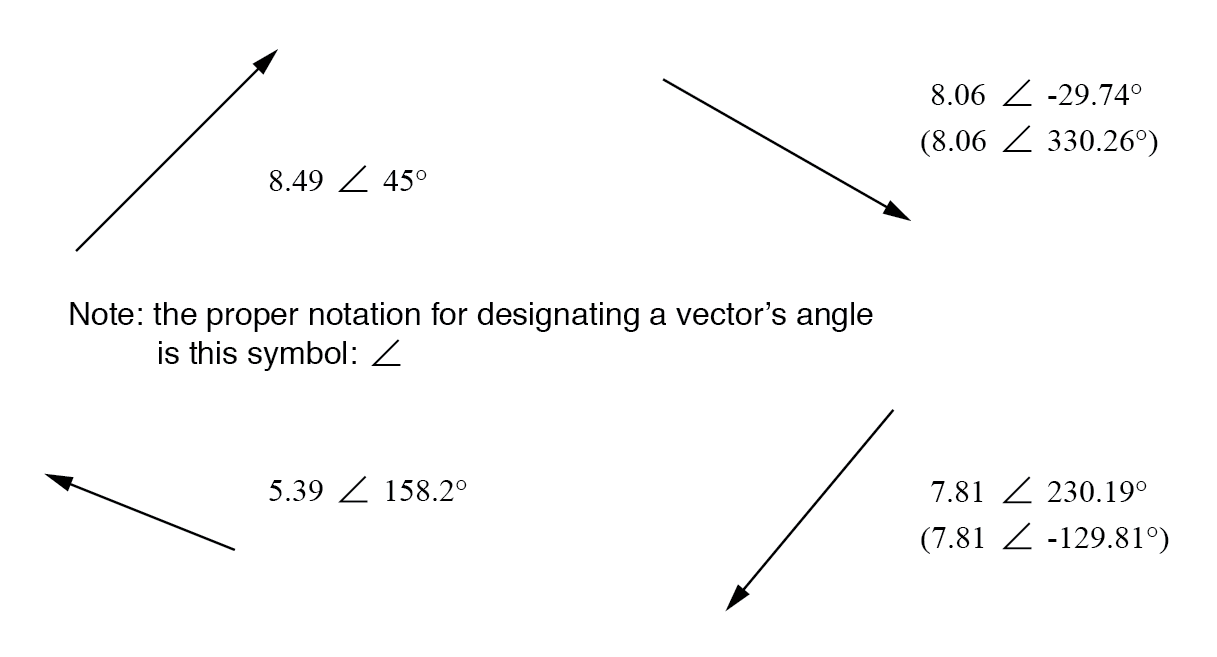
Vektor dengan notasi kutub.
Orientasi standar untuk sudut vektor dalam perhitungan rangkaian AC mendefinisikan 0 ° sebagai ke kanan (horizontal), membuat 90 ° lurus ke atas, 180 ° ke kiri, dan 270 ° lurus ke bawah. Harap dicatat bahwa vektor bersudut “bawah” dapat memiliki sudut yang direpresentasikan dalam bentuk kutub sebagai bilangan positif lebih dari 180, atau bilangan negatif kurang dari 180.
Sebagai contoh, sebuah vektor yang bersudut 270° (lurus ke bawah) dapat juga dikatakan memiliki sudut -90°. (Gambar di bawah) Vektor di atas di sebelah kanan (7,81 230,19°) juga dapat dilambangkan sebagai 7,81 -129,81°.
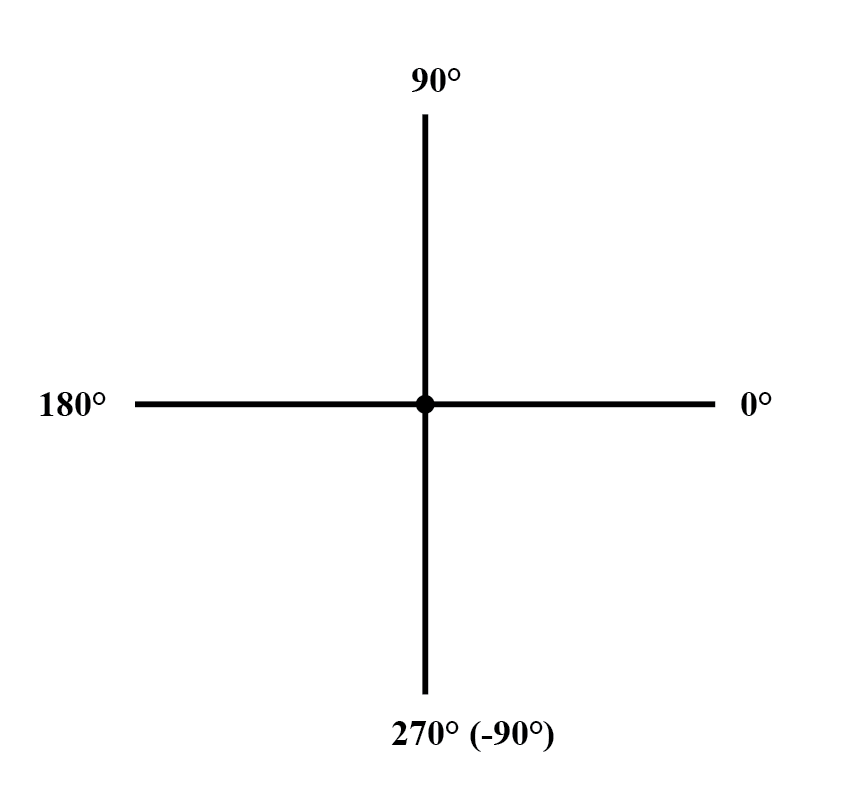
Kompas vektor.
Bentuk Persegi Panjang dari Bilangan Kompleks
Bentuk persegi panjang, di sisi lain, adalah di mana bilangan kompleks dilambangkan dengan komponen horizontal dan vertikal masing-masing. Pada dasarnya, vektor siku dianggap sebagai sisi miring dari segitiga siku-siku, dijelaskan oleh panjang sisi yang berdekatan dan yang berlawanan.
Daripada menggambarkan panjang dan arah vektor dengan menunjukkan besar dan sudut, ini dijelaskan dalam istilah "seberapa jauh kiri/kanan" dan "seberapa jauh atas/bawah."
Angka dua dimensi ini (horizontal dan vertikal) dilambangkan dengan dua angka numerik. Untuk membedakan dimensi horizontal dan vertikal satu sama lain, vertikal diawali dengan huruf kecil “i” (dalam matematika murni) atau “j” (dalam elektronik).
Huruf kecil ini tidak mewakili variabel fisik (seperti arus sesaat, juga dilambangkan dengan huruf kecil “i”), melainkan operator matematika digunakan untuk membedakan komponen vertikal vektor dari komponen horizontalnya. Sebagai bilangan kompleks lengkap, jumlah horizontal dan vertikal ditulis sebagai jumlah:(Gambar di bawah)
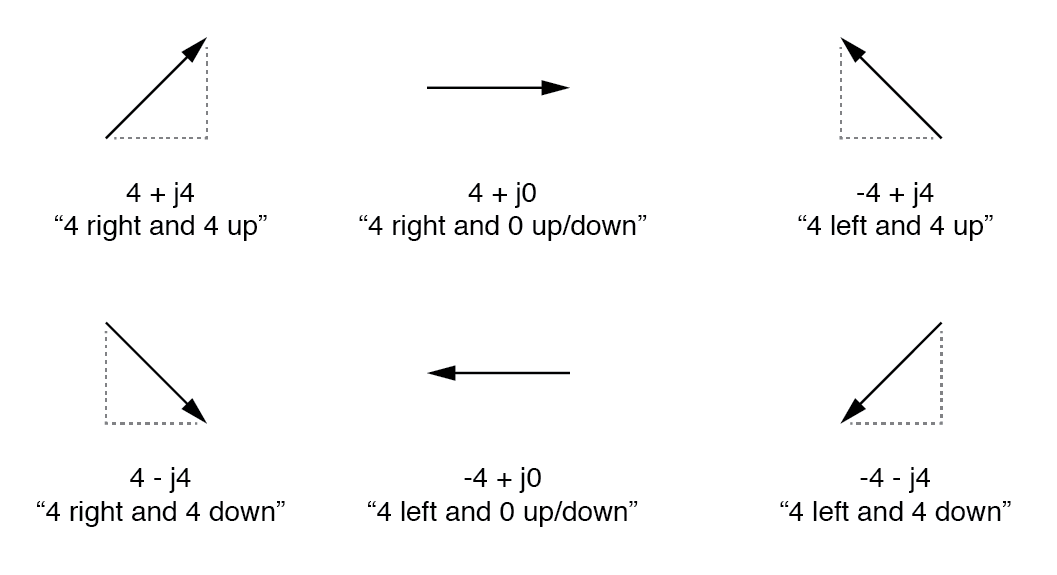
Dalam bentuk "persegi panjang" panjang dan arah vektor dilambangkan dengan rentang horizontal dan vertikal, angka pertama mewakili horizontal (“nyata”) dan yang kedua angka (dengan awalan "j") yang mewakili dimensi vertikal ("imajiner").
Komponen horizontal disebut sebagai nyata komponen karena dimensi tersebut kompatibel dengan bilangan normal, skalar (“nyata”). Komponen vertikal disebut sebagai imajiner komponen karena dimensi itu terletak pada arah yang berbeda, sama sekali asing dengan skala bilangan real. (Gambar di bawah)
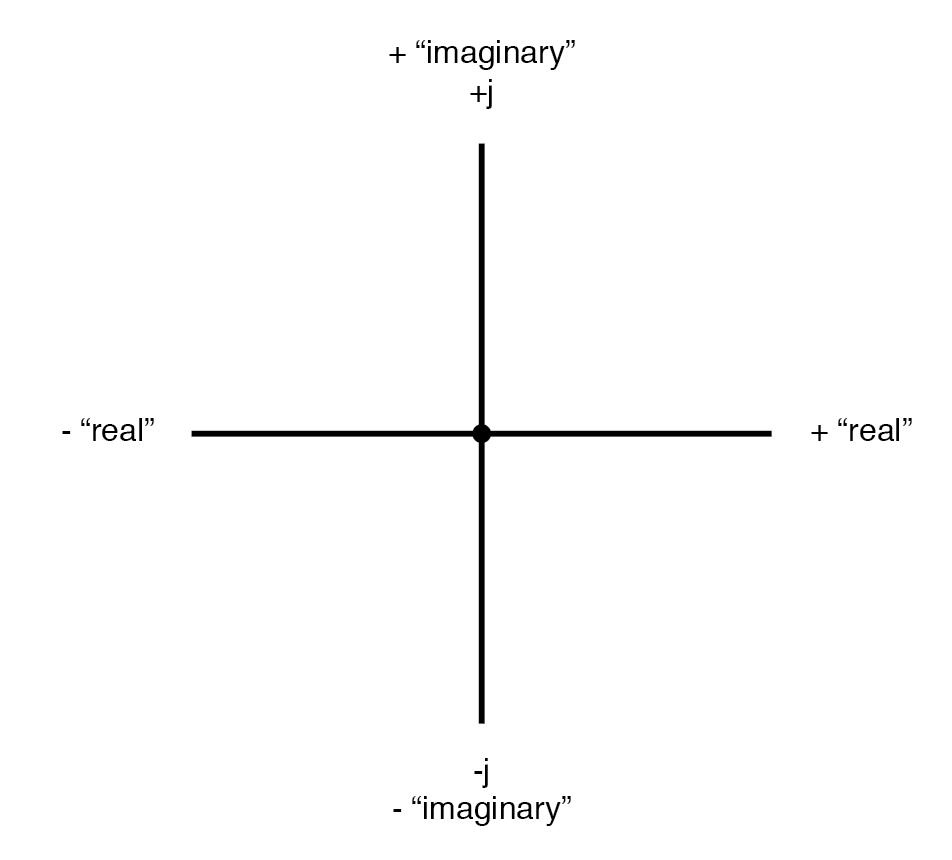
Kompas vektor menunjukkan sumbu nyata dan imajiner.
Sumbu "nyata" dari grafik sesuai dengan garis bilangan yang kita lihat sebelumnya:garis dengan nilai positif dan negatif di atasnya. Sumbu "imajiner" dari grafik sesuai dengan garis bilangan lain yang terletak pada 90° dengan garis "nyata".
Vektor sebagai benda dua dimensi, kita harus memiliki "peta" dua dimensi untuk mengekspresikannya, sehingga dua garis bilangan tegak lurus satu sama lain:(Gambar di bawah)
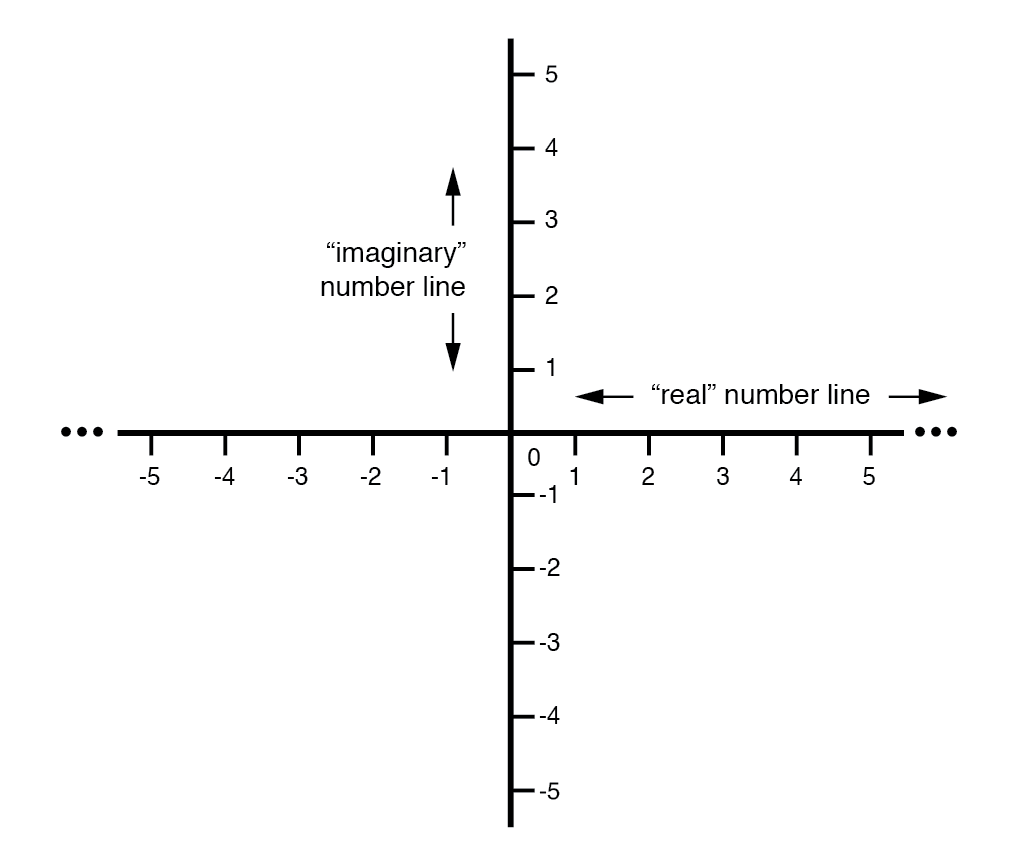
Kompas vektor dengan garis bilangan real dan imajiner (“j”).
Mengonversi dari Bentuk Kutub ke Bentuk Persegi Panjang
Metode notasi mana pun berlaku untuk bilangan kompleks. Alasan utama untuk memiliki dua metode notasi adalah untuk kemudahan perhitungan tangan, bentuk persegi panjang meminjamkan dirinya sendiri untuk penambahan dan pengurangan, dan bentuk kutub meminjamkan dirinya sendiri untuk perkalian dan pembagian.
Konversi antara dua bentuk notasi melibatkan trigonometri sederhana. Untuk mengubah dari kutub ke persegi panjang, temukan komponen nyata dengan mengalikan besaran kutub dengan kosinus sudut, dan komponen imajiner dengan mengalikan besaran kutub dengan sinus sudut.
Ini dapat dipahami lebih mudah dengan menggambar kuantitas sebagai sisi segitiga siku-siku, sisi miring dari segitiga yang mewakili vektor itu sendiri (panjang dan sudutnya terhadap horizontal yang merupakan bentuk kutub), sisi horizontal dan vertikal yang mewakili " komponen persegi panjang nyata" dan "imajiner", masing-masing:(Gambar di bawah)
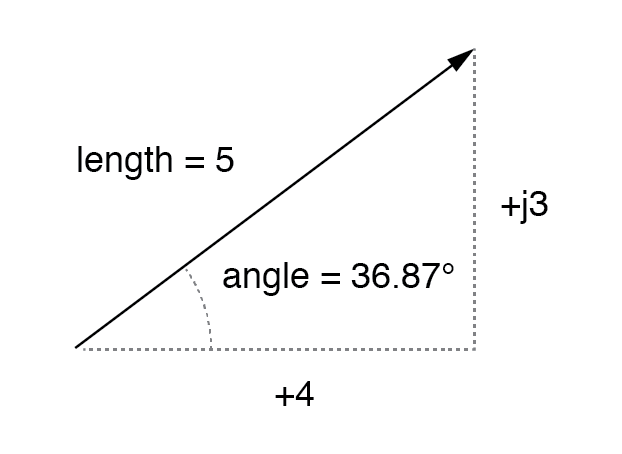
Vektor besaran dalam komponen real (4) dan imajiner (j3).

Mengonversi dari Bentuk Persegi Panjang ke Bentuk Kutub
Untuk mengubah dari persegi panjang ke kutub, temukan besaran kutub melalui penggunaan Teorema Pythagoras (besar kutub adalah sisi miring dari segitiga siku-siku, dan komponen nyata dan imajiner masing-masing adalah sisi yang berdekatan dan berlawanan), dan sudut oleh mengambil arctangent dari komponen imajiner dibagi dengan komponen real:
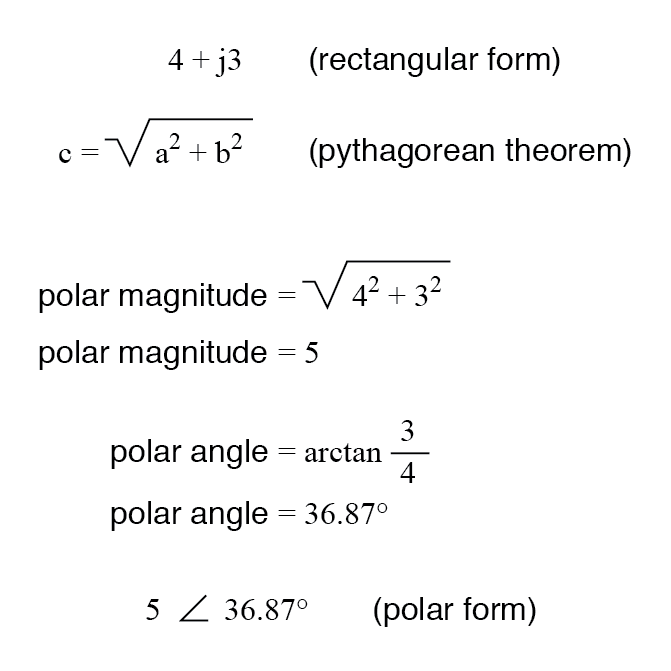
TINJAUAN:
- Kutub notasi menunjukkan bilangan kompleks dalam hal panjang vektor dan arah sudutnya dari titik awal. Contoh:terbang sejauh 45 mil 203° (Barat ke Barat Daya).
- Persegi Panjang notasi menunjukkan bilangan kompleks dalam hal dimensi horizontal dan vertikal. Contoh:berkendara sejauh 41 mil ke Barat, lalu belok dan kendarai sejauh 18 mil ke Selatan.
- Dalam notasi persegi panjang, besaran pertama adalah komponen “nyata” (dimensi horizontal vektor) dan besaran kedua adalah komponen “imajiner” (dimensi vertikal vektor). Komponen imajiner didahului oleh huruf kecil “j”, kadang-kadang disebut j operator .
- Bentuk notasi kutub dan persegi panjang untuk bilangan kompleks dapat dihubungkan secara grafis dalam bentuk segitiga siku-siku, dengan sisi miring mewakili vektor itu sendiri (bentuk kutub:sisi miring panjang =besaran; sudut terhadap sisi horizontal =sudut ), sisi horizontal mewakili komponen "nyata" persegi panjang, dan sisi vertikal mewakili komponen "imajiner" persegi panjang.
LEMBAR KERJA TERKAIT: