Memahami Minima Lokal dalam Pelatihan Jaringan Saraf

Artikel ini membahas komplikasi yang dapat mencegah Perceptron Anda mencapai akurasi klasifikasi yang memadai.

Dalam seri jaringan saraf AAC, kami telah membahas berbagai mata pelajaran yang terkait dengan pemahaman dan pengembangan jaringan saraf Perceptron multilayer. Sebelum membaca artikel ini di minima lokal, ikuti seri selanjutnya di bawah ini:

1. Bagaimana Melakukan Klasifikasi Menggunakan Jaringan Syaraf Tiruan:Apa Itu Perceptron?
2. Cara Menggunakan Contoh Jaringan Neural Perceptron Sederhana untuk Mengklasifikasikan Data
3. Cara Melatih Jaringan Neural Perceptron Dasar
4. Memahami Pelatihan Jaringan Syaraf Sederhana
5. Pengantar Teori Pelatihan untuk Jaringan Neural
6. Memahami Kecepatan Pembelajaran di Jaringan Neural
7. Pembelajaran Mesin Tingkat Lanjut dengan Perceptron Multilayer
8. Fungsi Aktivasi Sigmoid:Aktivasi di Jaringan Neural Perceptron Multilayer
9. Cara Melatih Jaringan Neural Perceptron Multilayer
10. Memahami Rumus Pelatihan dan Backpropagation untuk Perceptron Multilayer
11. Arsitektur Jaringan Saraf untuk Implementasi Python
12. Cara Membuat Jaringan Neural Perceptron Multilayer dengan Python
13. Pemrosesan Sinyal Menggunakan Jaringan Saraf Tiruan:Validasi dalam Desain Jaringan Saraf Tiruan
14. Pelatihan Kumpulan Data untuk Jaringan Neural:Cara Melatih dan Memvalidasi Jaringan Neural Python
15. Berapa Banyak Lapisan Tersembunyi dan Node Tersembunyi yang Dibutuhkan Jaringan Neural?
16. Cara Meningkatkan Akurasi Jaringan Neural Lapisan Tersembunyi
17. Menggabungkan Bias Node ke Jaringan Neural Anda
18. Memahami Minima Lokal dalam Pelatihan Jaringan Saraf

Pelatihan jaringan saraf adalah proses yang kompleks. Untungnya, kita tidak harus memahaminya dengan sempurna untuk mendapatkan manfaat darinya:arsitektur jaringan dan prosedur pelatihan yang kita gunakan benar-benar menghasilkan sistem fungsional yang mencapai akurasi klasifikasi yang sangat tinggi. Namun, ada satu aspek teoretis dari pelatihan yang, meskipun agak sulit dipahami, patut mendapat perhatian kita.

Kami akan menyebutnya “masalah minima lokal”.

Mengapa Minima Lokal Layak Mendapatkan Perhatian Kita?

Yah ... saya tidak yakin. Ketika saya pertama kali belajar tentang jaringan saraf, saya mendapatkan kesan bahwa minima lokal benar-benar merupakan hambatan yang signifikan untuk pelatihan yang sukses, setidaknya ketika kita berurusan dengan hubungan input-output yang kompleks. Namun, saya percaya bahwa penelitian terbaru meremehkan pentingnya minima lokal. Mungkin struktur jaringan dan teknik pemrosesan yang lebih baru telah mengurangi keparahan masalah, atau mungkin kita hanya memiliki pemahaman yang lebih baik tentang bagaimana jaringan saraf benar-benar menavigasi menuju solusi yang diinginkan.

Kami akan meninjau kembali status minimum lokal saat ini di akhir artikel ini. Untuk saat ini, saya akan menjawab pertanyaan saya sebagai berikut:Minima lokal layak mendapat perhatian kita karena, pertama, mereka membantu kita untuk berpikir lebih dalam tentang apa yang sebenarnya terjadi ketika kita melatih jaringan melalui penurunan gradien, dan kedua, karena minima lokal— atau setidaknya adalah —dianggap sebagai penghalang signifikan bagi keberhasilan implementasi jaringan saraf dalam sistem kehidupan nyata.

Apa itu Minimum Lokal?

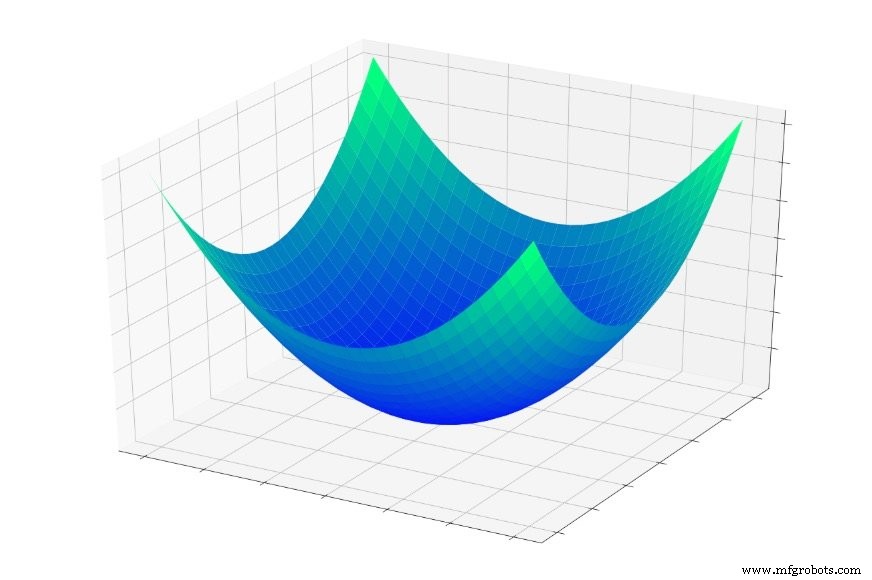
Di Bagian 5, kami mempertimbangkan "mangkuk kesalahan" yang ditunjukkan di bawah, dan saya menggambarkan pelatihan pada dasarnya sebagai pencarian titik terendah dalam mangkuk ini.

(Catatan :Sepanjang artikel ini, gambar dan penjelasan saya akan bergantung pada pemahaman intuitif kita tentang struktur tiga dimensi, tetapi perlu diingat bahwa konsep umum tidak terbatas pada hubungan tiga dimensi. Memang, kami sering menggunakan jaringan saraf yang dimensinya jauh melebihi dua variabel input dan satu variabel output.)

Jika Anda melompat ke dalam mangkuk ini, Anda akan meluncur ke bawah, setiap saat. Di mana pun Anda memulai , Anda akan berakhir di titik terendah dari seluruh fungsi kesalahan. Titik terendah ini adalah minimum global . Ketika sebuah jaringan telah konvergen pada minimum global, ia telah mengoptimalkan kemampuannya untuk mengklasifikasikan data pelatihan, dan secara teori , inilah tujuan dasar pelatihan:untuk terus memodifikasi bobot hingga minimum global tercapai.

Namun, kita tahu bahwa jaringan saraf mampu mendekati hubungan input-output yang sangat kompleks. Mangkuk kesalahan di atas tidak cocok dengan kategori "sangat kompleks". Ini hanyalah plot dari fungsi \(f(x,y) =x^2 + y^2\).

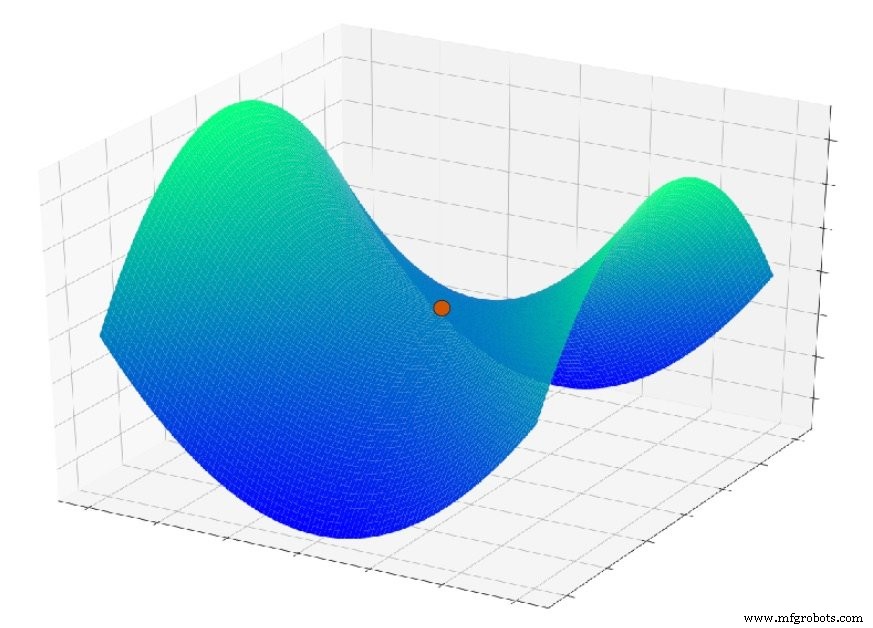
Tapi sekarang bayangkan bahwa fungsi kesalahan terlihat seperti ini:

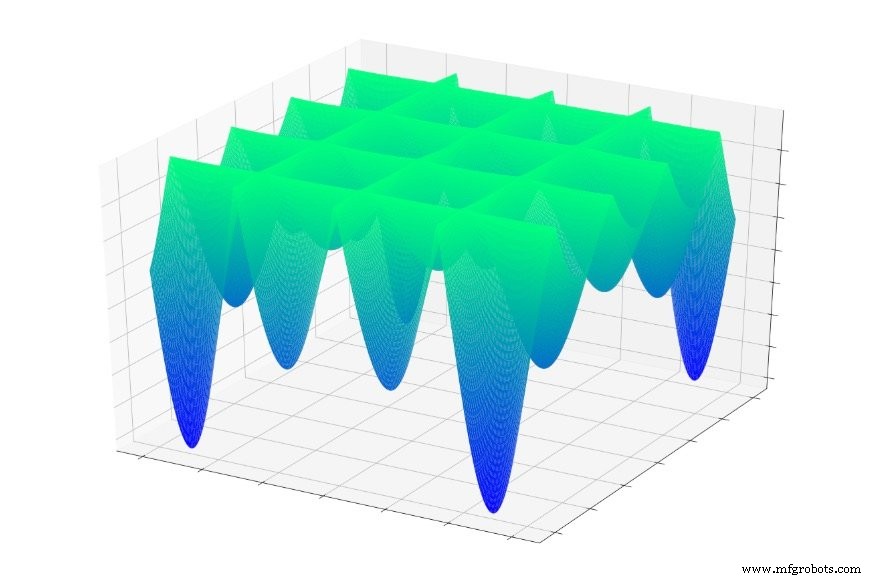
Atau ini:

Atau ini:

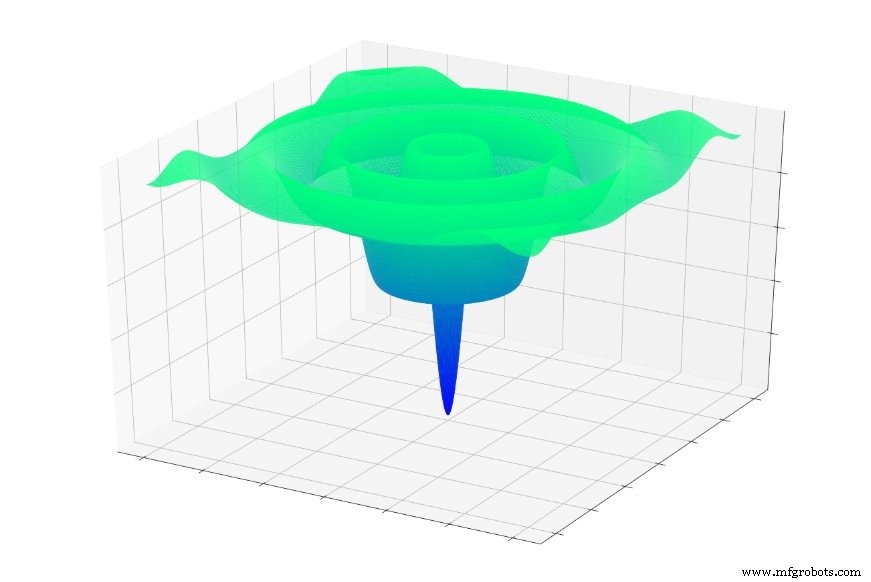
Jika Anda melompat secara acak ke salah satu fungsi ini, Anda akan sering meluncur ke bawah ke minimum lokal. Anda akan berada di titik terendah dari bagian grafik yang dilokalkan, tetapi Anda mungkin tidak berada di dekat global minimal.

Hal yang sama dapat terjadi pada jaringan saraf. Penurunan gradien bergantung pada lokal informasi yang, kami harap, akan memimpin jaringan menuju global minimum. Jaringan tidak memiliki pengetahuan sebelumnya tentang karakteristik permukaan kesalahan secara keseluruhan, dan akibatnya ketika mencapai titik yang tampak seperti bagian bawah permukaan kesalahan berdasarkan informasi lokal , ia tidak dapat mengeluarkan peta topografi dan menentukan bahwa ia perlu kembali menanjak untuk menemukan titik yang sebenarnya lebih rendah dari yang lainnya.

Saat kami menerapkan penurunan gradien dasar, kami memberi tahu jaringan, "Temukan bagian bawah permukaan kesalahan dan tetap di sana." Kami tidak mengatakan, “Temukan bagian bawah permukaan kesalahan, catat koordinat Anda, lalu terus mendaki menanjak dan turun sampai Anda menemukan yang berikutnya. Beri tahu saya jika Anda sudah selesai.”

Apakah Kita Benar-Benar Ingin Menemukan Minimum Global?

Masuk akal untuk mengasumsikan bahwa minimum global mewakili solusi optimal, dan untuk menyimpulkan bahwa minimum lokal bermasalah karena pelatihan mungkin "berhenti" di minimum lokal daripada melanjutkan ke minimum global.

Saya pikir asumsi ini valid dalam banyak kasus, tetapi penelitian yang cukup baru pada permukaan kehilangan jaringan saraf menunjukkan bahwa jaringan dengan kompleksitas tinggi sebenarnya dapat mengambil manfaat dari minima lokal, karena jaringan yang menemukan minimum global akan dilatih secara berlebihan dan oleh karena itu akan lebih sedikit efektif saat memproses sampel input baru.

Masalah lain yang berperan di sini adalah fitur permukaan yang disebut titik pelana; Anda dapat melihat contohnya pada plot di bawah ini. Ada kemungkinan bahwa dalam konteks aplikasi jaringan saraf nyata, titik pelana di permukaan kesalahan sebenarnya merupakan masalah yang lebih serius daripada minima lokal.

Kesimpulan

Saya harap Anda menikmati diskusi tentang minima lokal ini. Dalam artikel berikutnya, kita akan membahas beberapa teknik yang membantu jaringan saraf mencapai minimum global (jika memang itu yang kita inginkan).