Cara Meningkatkan Akurasi Jaringan Neural Lapisan Tersembunyi
Dalam artikel ini, kami akan melakukan beberapa eksperimen klasifikasi dan mengumpulkan data tentang hubungan antara dimensi lapisan tersembunyi dan kinerja jaringan.
Dalam artikel ini, Anda akan mempelajari cara memodifikasi lapisan tersembunyi untuk meningkatkan akurasi jaringan saraf menggunakan implementasi Python dan contoh masalah.
Namun, sebelum kita beralih ke subjek itu, pertimbangkan untuk mengikuti entri sebelumnya dalam seri ini tentang jaringan saraf:
- Bagaimana Melakukan Klasifikasi Menggunakan Jaringan Syaraf Tiruan:Apa Itu Perceptron?
- Cara Menggunakan Contoh Jaringan Neural Perceptron Sederhana untuk Mengklasifikasikan Data
- Cara Melatih Jaringan Neural Perceptron Dasar
- Memahami Pelatihan Jaringan Syaraf Sederhana
- Pengantar Teori Pelatihan untuk Jaringan Neural
- Memahami Kecepatan Pembelajaran di Jaringan Neural
- Pembelajaran Mesin Tingkat Lanjut dengan Perceptron Multilayer
- Fungsi Aktivasi Sigmoid:Aktivasi di Jaringan Neural Perceptron Multilayer
- Cara Melatih Jaringan Neural Perceptron Multilayer
- Memahami Rumus Pelatihan dan Backpropagation untuk Perceptron Multilayer
- Arsitektur Jaringan Saraf untuk Implementasi Python
- Cara Membuat Jaringan Neural Perceptron Multilayer dengan Python
- Pemrosesan Sinyal Menggunakan Jaringan Saraf Tiruan:Validasi dalam Desain Jaringan Saraf Tiruan
- Pelatihan Kumpulan Data untuk Jaringan Neural:Cara Melatih dan Memvalidasi Jaringan Neural Python
- Berapa Banyak Lapisan Tersembunyi dan Node Tersembunyi yang Dibutuhkan Jaringan Neural?
- Cara Meningkatkan Akurasi Jaringan Neural Lapisan Tersembunyi
Jumlah node yang termasuk dalam lapisan tersembunyi mempengaruhi kemampuan klasifikasi dan kecepatan jaringan syaraf tiruan Perceptron. Kami akan menjalankan eksperimen yang akan membantu kami merumuskan beberapa intuisi baru tentang bagaimana dimensi lapisan tersembunyi cocok dengan upaya merancang jaringan yang berlatih dalam jumlah waktu yang wajar, menghasilkan nilai keluaran dengan latensi yang dapat diterima, dan memenuhi persyaratan akurasi .
Pembandingan dengan Python
Kode Python jaringan saraf yang disajikan di Bagian 12 sudah menyertakan bagian yang menghitung akurasi dengan menggunakan jaringan terlatih untuk mengklasifikasikan sampel dari kumpulan data validasi. Jadi, yang perlu kita lakukan hanyalah menambahkan beberapa kode yang akan melaporkan waktu eksekusi untuk pelatihan (yang mencakup operasi feedforward dan backpropagation) dan untuk fungsionalitas klasifikasi aktual (yang hanya mencakup operasi feedforward). Kami akan menggunakan time.perf_counter() fungsi untuk ini.
Inilah cara saya menandai awal dan akhir pelatihan:
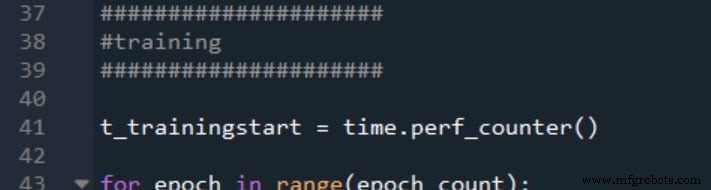
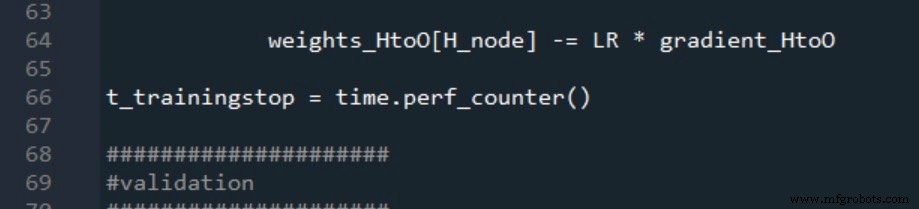
Waktu mulai dan berhenti validasi dibuat dengan cara yang sama:
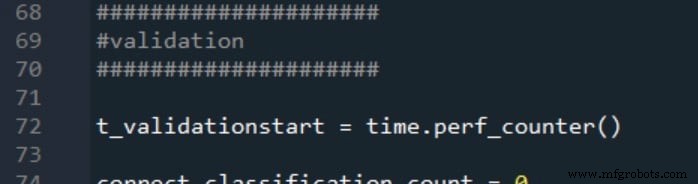

Dua pengukuran waktu pemrosesan dilaporkan sebagai berikut:
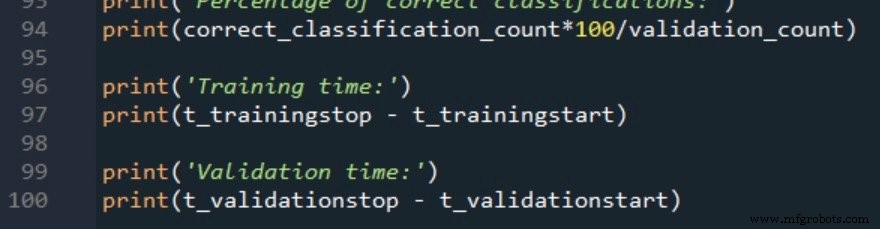
Data Pelatihan dan Prosedur Pengukuran
Jaringan saraf akan melakukan klasifikasi benar/salah pada sampel input yang terdiri dari empat nilai numerik antara –20 dan +20.
Jadi, kita memiliki empat node input dan satu node output, dan nilai input dihasilkan dengan persamaan Excel yang ditunjukkan di bawah ini.
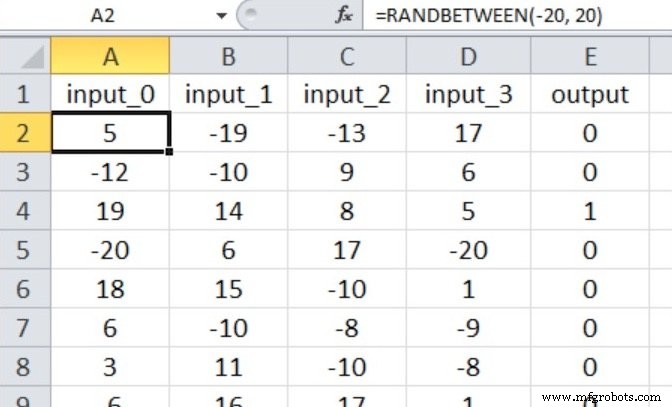
Kumpulan data pelatihan saya terdiri dari 40.000 sampel, dan kumpulan validasi memiliki 5000 sampel. Tingkat pembelajarannya adalah 0,1, dan saya hanya melakukan satu periode pelatihan.
Kami akan melakukan tiga eksperimen yang mewakili hubungan input-output dengan berbagai tingkat kerumitan. np.random.seed(1) pernyataan dikomentari, sehingga nilai bobot awal akan bervariasi dan demikian juga akurasi klasifikasi.
Dalam setiap percobaan, program akan dieksekusi lima kali (dengan data pelatihan dan validasi yang sama) untuk setiap dimensi lapisan tersembunyi, dan pengukuran akhir untuk akurasi dan waktu pemrosesan akan menjadi rata-rata aritmatika dari hasil yang dihasilkan oleh lima proses terpisah. .
Eksperimen 1:Masalah Kompleksitas Rendah
Dalam percobaan ini, output benar hanya jika tiga input pertama lebih besar dari nol, seperti yang ditunjukkan pada screenshot Excel di bawah ini (perhatikan bahwa input keempat tidak berpengaruh pada nilai output).
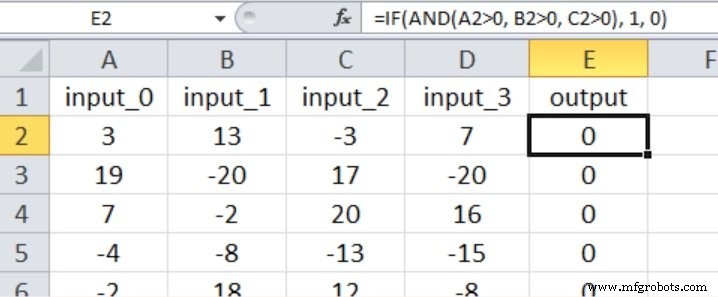
Saya pikir ini memenuhi syarat sebagai hubungan input-output yang cukup sederhana untuk Perceptron multilayer.
Berdasarkan rekomendasi yang saya berikan di Bagian 15 mengenai berapa banyak lapisan dan node yang dibutuhkan jaringan saraf, saya akan mulai dengan dimensi lapisan tersembunyi yang sama dengan dua pertiga dimensi masukan.
Karena saya tidak dapat memiliki lapisan tersembunyi dengan sebagian kecil dari sebuah simpul, saya akan mulai dari H_dim =2 . Tabel di bawah menyajikan hasilnya.
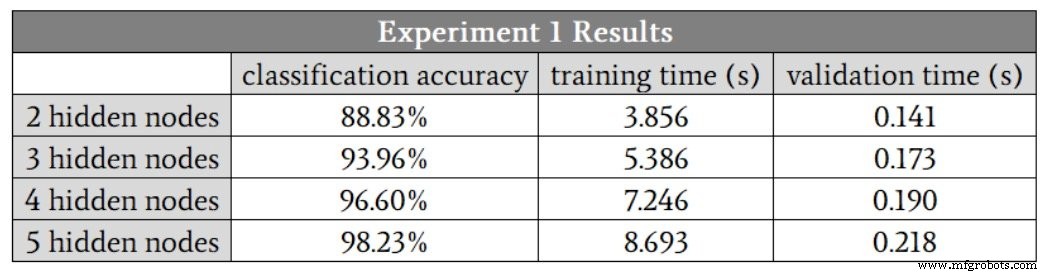
Kami melihat peningkatan klasifikasi sampai ke lima node tersembunyi. Namun, menurut saya angka-angka ini melebih-lebihkan manfaat peningkatan dari empat menjadi lima node, karena akurasi salah satu dari empat-tersembunyi-node berjalan adalah 88,6%, dan ini menyeret turun rata-rata.
Jika saya menghilangkan proses akurasi rendah itu, akurasi rata-rata untuk empat node tersembunyi sebenarnya sedikit lebih tinggi daripada rata-rata untuk lima node tersembunyi. Saya menduga bahwa dalam kasus ini, empat node tersembunyi akan memberikan keseimbangan terbaik antara akurasi dan kecepatan.
Hal penting lainnya yang perlu diperhatikan dalam hasil ini adalah perbedaan bagaimana dimensi lapisan tersembunyi memengaruhi waktu pelatihan dan waktu pemrosesan. Berpindah dari dua ke empat node tersembunyi meningkatkan waktu validasi dengan faktor 1,3, tetapi meningkatkan waktu pelatihan dengan faktor 1,9.
Pelatihan secara signifikan lebih intensif secara komputasi daripada pemrosesan feedforward, jadi kami harus sangat memperhatikan bagaimana konfigurasi jaringan memengaruhi kemampuan kami untuk melatih jaringan dalam jumlah waktu yang wajar.
Eksperimen 2:Masalah Kompleksitas Sedang
Tangkapan layar Excel menunjukkan hubungan input-output untuk eksperimen ini. Keempat input sekarang memengaruhi nilai output, dan perbandingannya tidak sesederhana pada Eksperimen 1.
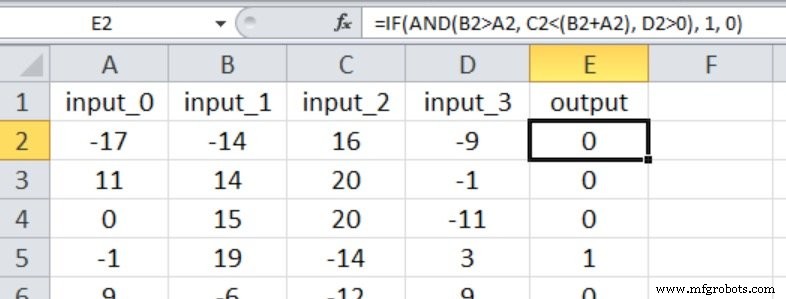
Saya mulai dengan tiga simpul tersembunyi. Berikut adalah hasilnya:
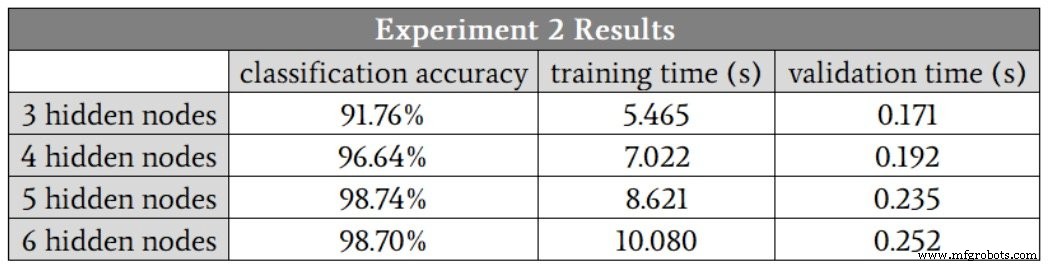
Dalam hal ini, saya menduga bahwa lima node tersembunyi akan memberi kita kombinasi akurasi dan kecepatan terbaik, meskipun sekali lagi menjalankan empat node tersembunyi menghasilkan satu nilai akurasi yang jauh lebih rendah daripada yang lain. Jika Anda mengabaikan pencilan ini, hasil untuk empat simpul tersembunyi, lima simpul tersembunyi, dan enam simpul tersembunyi akan terlihat sangat mirip.
Fakta bahwa lima-tersembunyi-node dan enam-tersembunyi-node berjalan tidak menghasilkan outlier membawa kita ke temuan yang mungkin menarik:mungkin meningkatkan dimensi lapisan tersembunyi membuat jaringan lebih kuat terhadap kondisi yang untuk beberapa alasan menyebabkan pelatihan untuk menjadi sangat sulit.
Eksperimen 3:Masalah Kompleksitas Tinggi
Seperti yang ditunjukkan di bawah ini, hubungan input-output yang baru kembali mencakup keempat nilai input, dan kami telah memperkenalkan nonlinier dengan mengkuadratkan salah satu input dan mengambil akar kuadrat dari input lainnya.
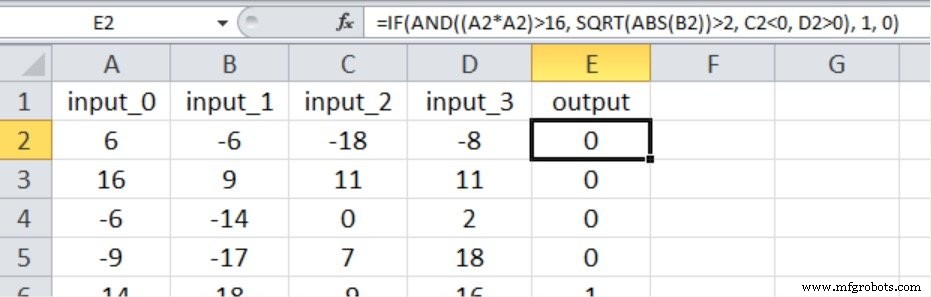
Berikut adalah hasilnya:
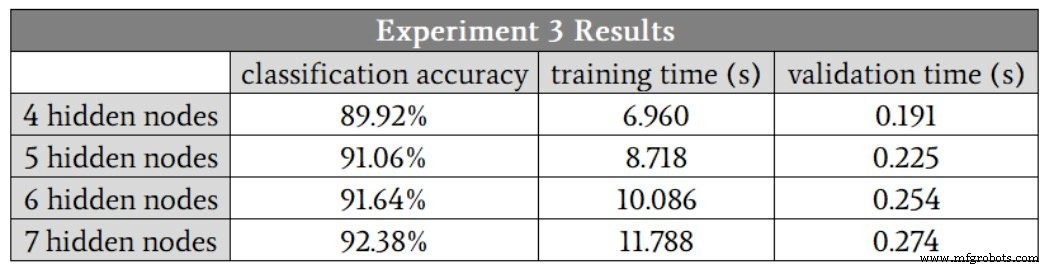
Jaringan pasti memiliki lebih banyak kesulitan dengan hubungan matematis dengan kompleksitas yang lebih tinggi ini; bahkan dengan tujuh node tersembunyi, akurasinya lebih rendah daripada yang kami capai dengan hanya tiga node tersembunyi dalam masalah kompleksitas rendah. Saya yakin bahwa kami dapat meningkatkan kinerja dengan kompleksitas tinggi dengan memodifikasi aspek lain dari jaringan—misalnya, termasuk bias (lihat Bagian 11) atau menggabungkan kecepatan pembelajaran (lihat Bagian 6).
Namun demikian, saya akan menjaga dimensi lapisan tersembunyi di tujuh sampai saya benar-benar yakin bahwa peningkatan lain dapat memungkinkan jaringan untuk mempertahankan kinerja yang memadai dengan lapisan tersembunyi yang lebih kecil.
Kesimpulan
Kami telah melihat beberapa pengukuran menarik yang melukiskan gambaran yang cukup jelas tentang hubungan antara dimensi lapisan tersembunyi dan kinerja Perceptron. Tentu saja ada lebih banyak detail yang dapat kami jelajahi, tetapi menurut saya ini memberi Anda beberapa informasi dasar yang kuat yang dapat Anda gunakan saat bereksperimen dengan desain dan pelatihan jaringan saraf.















