Memahami Rumus Pelatihan dan Backpropagation untuk Perceptron Multilayer

Artikel ini menyajikan persamaan yang kami gunakan saat melakukan perhitungan pembaruan bobot, dan kami juga akan membahas konsep backpropagation.

Selamat datang di seri AAC tentang pembelajaran mesin.

Ikuti serinya sejauh ini di sini:

1. Bagaimana Melakukan Klasifikasi Menggunakan Jaringan Syaraf Tiruan:Apa Itu Perceptron?
2. Cara Menggunakan Contoh Jaringan Neural Perceptron Sederhana untuk Mengklasifikasikan Data
3. Cara Melatih Jaringan Neural Perceptron Dasar
4. Memahami Pelatihan Jaringan Syaraf Sederhana
5. Pengantar Teori Pelatihan untuk Jaringan Neural
6. Memahami Kecepatan Pembelajaran di Jaringan Neural
7. Pembelajaran Mesin Tingkat Lanjut dengan Perceptron Multilayer
8. Fungsi Aktivasi Sigmoid:Aktivasi di Jaringan Neural Perceptron Multilayer
9. Cara Melatih Jaringan Neural Perceptron Multilayer
10. Memahami Rumus Pelatihan dan Backpropagation untuk Perceptron Multilayer
11. Arsitektur Jaringan Saraf untuk Implementasi Python
12. Cara Membuat Jaringan Neural Perceptron Multilayer dengan Python
13. Pemrosesan Sinyal Menggunakan Jaringan Saraf Tiruan:Validasi dalam Desain Jaringan Saraf Tiruan
14. Pelatihan Kumpulan Data untuk Jaringan Neural:Cara Melatih dan Memvalidasi Jaringan Neural Python

Kami telah mencapai titik di mana kami perlu mempertimbangkan dengan cermat topik mendasar dalam teori jaringan saraf:prosedur komputasi yang memungkinkan kami untuk menyempurnakan bobot Perceptron (MLP) multilayer sehingga dapat mengklasifikasikan sampel input secara akurat. Ini akan membawa kita pada konsep “backpropagation”, yang merupakan aspek penting dari desain jaringan saraf.

Memperbarui Bobot

Informasi seputar pelatihan untuk MLP rumit. Lebih buruk lagi, sumber daya online menggunakan terminologi dan simbol yang berbeda, dan mereka bahkan tampaknya memberikan hasil yang berbeda. Namun, saya tidak yakin apakah hasilnya benar-benar berbeda atau hanya menyajikan informasi yang sama dengan cara yang berbeda.

Persamaan yang terkandung dalam artikel ini didasarkan pada derivasi dan penjelasan yang diberikan oleh Dr. Dustin Stansbury dalam posting blog ini. Perlakuannya adalah yang terbaik yang saya temukan, dan ini adalah tempat yang bagus untuk memulai jika Anda ingin mempelajari detail matematis dan konseptual dari penurunan gradien dan propagasi balik.

Diagram berikut mewakili arsitektur yang akan kita implementasikan dalam perangkat lunak, dan persamaan di bawah ini sesuai dengan arsitektur ini, yang akan dibahas lebih mendalam di artikel berikutnya.

Terminologi

Topik ini dengan cepat menjadi tidak terkendali jika kita tidak mempertahankan terminologi yang jelas. Saya akan menggunakan istilah berikut:

• Praaktivasi (disingkat \(S_{preA}\) ):Ini mengacu pada sinyal (sebenarnya hanya angka dalam konteks satu iterasi pelatihan) yang berfungsi sebagai input ke fungsi aktivasi node. Ini dihitung dengan melakukan produk titik dari array yang berisi bobot dan array yang berisi nilai yang berasal dari node di lapisan sebelumnya. Perkalian titik setara dengan melakukan perkalian elemen dua larik dan kemudian menjumlahkan elemen dalam larik yang dihasilkan dari perkalian itu.
• Pasca-aktivasi (disingkat \(S_{postA}\) ):Ini mengacu pada sinyal (sekali lagi, hanya angka dalam konteks iterasi individu) yang keluar dari node. Ini dihasilkan dengan menerapkan fungsi aktivasi ke sinyal praaktivasi. Istilah pilihan saya untuk fungsi aktivasi, dilambangkan dengan \(f_{A}()\) , adalah logistik daripada sigmoid.
• Dalam kode Python, Anda akan melihat matriks bobot berlabel ItoH dan HtoO . Saya menggunakan pengidentifikasi ini karena ambigu untuk mengatakan sesuatu seperti "bobot lapisan tersembunyi"—apakah ini bobot yang diterapkan sebelum lapisan tersembunyi atau setelah lapisan tersembunyi? Dalam skema saya, ItoH menentukan bobot yang diterapkan pada nilai yang ditransfer dari node input ke node tersembunyi, dan HtoO menentukan bobot yang diterapkan pada nilai yang ditransfer dari node tersembunyi ke node output.
• Nilai keluaran yang benar untuk sampel pelatihan disebut sebagai target dan dilambangkan dengan T .
• Kecepatan pembelajaran disingkat sebagai LR .
• Kesalahan terakhir adalah perbedaan antara sinyal pascaaktivasi dari simpul keluaran (\(S_{postA,O}\) ) dan target, dihitung sebagai \(FE =S_{postA,O} - T\) .
• Sinyal kesalahan (\(S_{KESALAHAN}\) ) adalah kesalahan terakhir yang disebarkan kembali ke lapisan tersembunyi melalui fungsi aktivasi dari simpul keluaran.
• Gradien mewakili kontribusi bobot yang diberikan pada sinyal kesalahan. Kami memodifikasi bobot dengan mengurangi kontribusi ini (dikalikan dengan kecepatan pembelajaran jika perlu).

Diagram berikut menempatkan beberapa istilah ini dalam konfigurasi jaringan yang divisualisasikan. Saya tahu—kelihatannya seperti kekacauan warna-warni. Saya minta maaf. Ini adalah diagram padat informasi, dan meskipun sekilas mungkin sedikit menyinggung, jika Anda mempelajarinya dengan cermat, saya pikir Anda akan merasa sangat membantu.

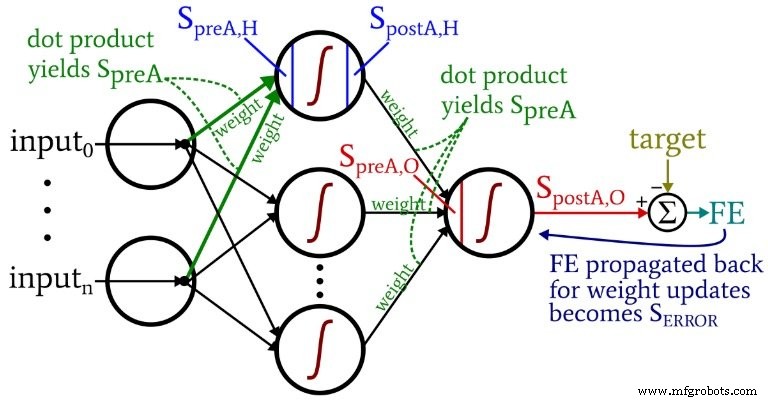
Persamaan pembaruan bobot diturunkan dengan mengambil turunan parsial dari fungsi kesalahan (kami menggunakan kesalahan kuadrat yang dijumlahkan, lihat Bagian 8 dari seri, yang berhubungan dengan fungsi aktivasi) sehubungan dengan bobot yang akan dimodifikasi. Silakan merujuk ke posting Dr. Stansbury jika Anda ingin melihat matematika; dalam artikel ini kita akan langsung menuju ke hasil. Untuk bobot hidden-to-output, kami memiliki yang berikut:

\[S_{ERROR} =FE \times {f_A}'(S_{preA,O})\]

\[gradient_{HtoO}=S_{ERROR}\times S_{postA,H}\]

\[weight_{HtoO} =weight_{HtoO}- (LR \times gradient_{HtoO})\]

Kami menghitung tanda kesalahan l dengan mengalikan kesalahan akhir dengan nilai yang dihasilkan saat kita menerapkan turunan fungsi aktivasi ke sinyal praaktivasi dikirim ke simpul keluaran (perhatikan simbol prima, yang menunjukkan turunan pertama, di \({f_A}'(S_{preA,O})\)). gradien kemudian dihitung dengan mengalikan sinyal kesalahan oleh sinyal pascaaktivasi dari lapisan tersembunyi. Terakhir, kami memperbarui bobot dengan mengurangi gradien dari nilai bobot saat ini, dan kita dapat mengalikan gradien dengan kecepatan pembelajaran jika kita ingin mengubah ukuran langkah.

Untuk bobot input-to-hidden, kita memiliki ini:

\[gradient_{ItoH} =FE \times {f_A}'(S_{preA,O})\times weight_{HtoO} \times {f_A}'(S_{preA ,H}) \kali masukan\]

\[\Rightarrow gradient_{ItoH} =S_{ERROR} \times weight_{HtoO} \times {f_A}'(S_{preA,H})\times input\]

\[weight_{ItoH} =weight_{ItoH} - (LR \times gradient_{ItoH})\]

Dengan bobot masukan-ke-tersembunyi, kesalahan harus disebarkan kembali melalui lapisan tambahan, dan kami melakukannya dengan mengalikan sinyal kesalahan dengan bobot tersembunyi-ke-output terhubung ke simpul tersembunyi yang menarik. Jadi, jika kami memperbarui bobot masukan-ke-tersembunyi yang mengarah ke simpul tersembunyi pertama, kami mengalikan sinyal kesalahan dengan bobot yang menghubungkan simpul tersembunyi pertama ke simpul keluaran. Kami kemudian menyelesaikan perhitungan dengan melakukan perkalian yang analog dengan pembaruan bobot tersembunyi-ke-output:kami menerapkan turunan dari fungsi aktivasi ke sinyal praaktivasi node tersembunyi , dan nilai “input” dapat dianggap sebagai sinyal pascaaktivasi dari simpul masukan.

Propagasi balik

Penjelasan di atas sudah menyentuh konsep backpropagation. Saya hanya ingin memperkuat konsep ini secara singkat dan juga memastikan bahwa Anda memiliki pemahaman yang jelas tentang istilah ini, yang sering muncul dalam diskusi tentang jaringan saraf.

Backpropagation memungkinkan kita untuk mengatasi dilema hidden-node yang dibahas di Bagian 8. Kita perlu memperbarui bobot input-to-hidden berdasarkan perbedaan antara output yang dihasilkan jaringan dan nilai output target yang disediakan oleh data pelatihan, tetapi bobot ini mempengaruhi output yang dihasilkan secara tidak langsung.

Backpropagation mengacu pada teknik di mana kami mengirim sinyal kesalahan kembali ke satu atau lebih lapisan tersembunyi dan skala sinyal kesalahan itu menggunakan bobot yang muncul dari simpul tersembunyi dan turunan dari fungsi aktivasi simpul tersembunyi. Prosedur keseluruhan berfungsi sebagai cara memperbarui bobot berdasarkan kontribusi bobot terhadap kesalahan keluaran, meskipun kontribusi tersebut dikaburkan oleh hubungan tidak langsung antara bobot input-ke-tersembunyi dan nilai output yang dihasilkan.

Kesimpulan

Kami telah membahas banyak materi penting. Saya pikir kami memiliki beberapa informasi yang sangat berharga tentang pelatihan jaringan saraf di artikel ini, dan saya harap Anda setuju. Serial ini akan semakin seru, jadi periksa kembali untuk angsuran baru.