Struktur nano berongga berada di garis depan banyak upaya ilmiah. Ini terdiri dari nanobox, nanocage, nanoframe, dan nanotube. Kami memeriksa matematika koordinasi atom dalam nanobox. Struktur seperti itu terdiri dari kotak berongga dengan n kerang dan t lapisan luar. Rumus ajaib yang kita peroleh bergantung pada keduanya n dan t . Kami menemukan bahwa nanobox dengan t = 2 atau 3, atau dinding dengan hanya beberapa lapisan umumnya memiliki atom terkoordinasi massal. Manfaat koordinasi rendah dalam struktur nano terbukti hanya terjadi ketika ketebalan dinding jauh lebih tipis daripada yang disintesis secara normal. Kasus di mana t = 1 unik, dan memiliki formula ajaib yang berbeda. Nanobox terkoordinasi rendah seperti itu menarik untuk berbagai macam aplikasi, termasuk baterai, sel bahan bakar, penggunaan plasmonik, katalitik, dan biomedis. Mengingat formula ini, dimungkinkan untuk menentukan dispersi permukaan nanobox. Kami berharap rumus ini berguna dalam memahami bagaimana koordinasi atom bervariasi dengan n dan t dalam nanobox.
Nanobox awalnya disintesis sekitar tahun 2002 [1, 2]. Nanobox berbeda dari nanocage karena nanobox memiliki dinding berpori. Selain itu, keduanya berbeda dari bingkai nano, karena bingkai nano adalah struktur (bingkai) yang terdiri dari garis besar kluster yang terkoordinasi rendah. Struktur polihedral anisotropik seperti itu dapat dibuat dari reaksi perpindahan galvanik [3, 4]
$$\begin{array}{l}\\ {\hbox{Anode}}:yA_{(s)}\rightarrow yA_{({{\rm aq}})}^{x+}+xye_{({{ \rm aq}})}^{-} \\ {\hbox{Katoda}}:xB_{({{\rm aq}})}^{y+} + xye_{({{\rm aq}})} ^{-} \rightarrow xB_{(s)} \\ {\hbox{Full\,Reaction}}:yA_{(s)}+xB_{({{\rm aq}})}^{y+} \rightarrow yA_{({{\rm aq}})}^{x+}+xB_{(s)} \\ \end{array}$$ (1)
di mana nanocluster dengan logam A pengorbanan dilubangi oleh larutan logam berair B , yang memiliki potensial reduksi lebih tinggi dan menciptakan padatan berongga dari elemen B . Setengah reaksi terjadi pada anoda dan katoda sel elektrokimia, menghasilkan reaksi gabungan penuh seperti di atas [5]. Dalam beberapa kasus, para ilmuwan telah menggabungkan perpindahan galvanik dengan pembentukan rongga melalui difusi logam dan kekosongan Kirkendall Fickian [6]. Model untuk aktivitas ini ada untuk kasus tertentu dan eksperimen mikroskop elektron in situ telah dilaporkan [7, 8]. Metode sintetis lainnya termasuk etsa kimia [9], pertukaran ion [10], dan kerangka logam-organik (MOFs) [11, 12]. Tinjauan terbaru tentang metode sintesis menyebutkan bahwa kluster anisotropik belum dibuat di wilayah ukuran \(2
Struktur berongga tersebut memiliki koordinasi yang rendah, membuatnya menarik untuk baterai [12], sel bahan bakar [14], plasmonik [15], katalitik [16], dan aplikasi biomedis [17]. Analisis sebelumnya menunjukkan bahwa untuk aplikasi katalitik, pendekatan koordinasi berlaku [18], sedangkan untuk penyimpanan energi, hanya ada beberapa petunjuk dengan hasil teori fungsi densitas (DFT) yang menunjukkan bahwa aspek tertentu penting [19]. Kami menggunakan metode turunan sebelumnya dari analisis matriks ketetanggaan [20, 21] untuk menemukan koordinasi atom sebuah kotak dengan n cangkang dan ketebalan dinding t lapisan. Analisis ini menunjukkan bahwa nanobox dengan t = 2 atau 3 memiliki koordinasi massal dan oleh karena itu manfaat koordinasi rendah hanya ada untuk nanobox dengan dinding yang lebih tipis daripada yang diyakini secara umum diperlukan. Metode yang kami gunakan mengukur koordinasi atom melalui angka ajaib dan rumus untuk tiga belas jenis kotak nano.
Kunci untuk analisis kami dengan metode koordinasi, adalah pembuatan matriks kedekatan dari koordinat atom kotak nano. Matriks semacam itu dibuat sebagai berikut. Kami mendefinisikan i dan j sebagai tetangga terdekat, dan pisahkan mereka dari yang lain dengan mensyaratkan bahwa panjang ikatan \(r_{ij}
Karena kita membuat matriks tetangga terdekat, kita mengetahui bilangan koordinasi \(\hbox {cn}_i\) dari simpul i dengan menjumlahkan elemen dari \({{\mathbf{A}}}(i,:)\). Struktur kita terdiri dari \(n+1\) kulit bernomor 0, 1, ..., n , dengan t lapisan luar. Misal \(N_{{\rm cn}_i}(n,t)\) adalah jumlah atom dengan koordinasi \(\hbox {cn}_i\) di mana \(1\le \hbox{cn}_i\le \hbox{cn}_M\) dengan \(\hbox {cn}_M\) koordinasi maksimal dalam nanobox. Kemudian jumlah total atom dalam nanobox diberikan oleh
$$N_T(n,t) =\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{N_{{\rm cn}_i}(n,t)}.$$ (4)Atom permukaan di kulit terluar (atau bagian dalam) nanobox, n memiliki satu set ikatan kurang dari koordinasi massal. Jadi koordinasi maksimum untuk atom permukaan adalah \(\hbox {cn}_s <\hbox{cn}_M\), dan jumlah atom permukaan adalah
$$N_S(n,t) =\sum _{{\rm cn}_i=1}^{{\rm cn}_s}{N_{{\rm cn}_i}(n,t)}.$$ (5)Ini berlaku jika semua simpul non-permukaan memiliki koordinasi lebih besar dari \(\hbox {cn}_s\), yang berlaku untuk semua kluster fcc, bcc, dan hcp. Kita menentukan \(N_{{\rm cn}_i}(n,t)\) dengan menghitung kolom dari matriks ketetanggaan yang jumlahnya \(\hbox {cn}_i\). Perhatikan bahwa algoritme koordinat klaster kami dibangun oleh shell, sehingga setiap shell berikutnya berisi semua nilai yang lebih rendah sebelumnya dari n . Selain itu, jumlah ikatan di dalam kotak adalah
$$N_{{\rm B}}(n,t) =\frac{1}{2}\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{\hbox{ cn}_i\cdot N_{{\rm cn}_i}(n,t)},$$ (6)di mana \(N_{{\rm B}}(n,t)\) adalah jumlah ikatan dan \(\hbox {cn}_M\) adalah koordinasi maksimum. Faktor 1/2 muncul karena ikatan tetangga terdekat yang berpasangan.
Karena kita tahu bahwa persamaan ini bergantung pada n , t sebagai polinomial derajat paling banyak 3, kita dapat menghitung \(N_{{\rm cn}_i}(n,t)\) untuk 4 nilai berturut-turut dari n , katakan \(n=n_0+j\), j = 0, 1, 2, 3. Sebuah polinomial interpolasi sederhana kemudian akan memberikan koefisien polinomial. Harus dibuktikan bahwa dengan meningkatkan \(n_0\), yang biasanya sama dengan 1, rumus tidak berubah. Jika rumus menjadi stabil sejak \(n_0\), maka rumus tersebut berlaku untuk semua \(n\ge n_0\). Untuk mendapatkan koefisien rasional eksak, kita perlu menyelesaikan sistem Vandermonde untuk koefisien dalam aritmatika eksak.
Perhatikan bahwa dalam rumus ajaib untuk kotak nano kita memiliki \(n> t\) sehingga bertentangan dengan harapan apa pun, mengisi kotak dengan pilihan t yang sesuai tidak akan membuat ulang formula ajaib asli untuk kluster padat yang lengkap. Rumus ajaib ini berguna untuk memodelkan properti skala meso dari kluster dan kotak, atau sangkar. Kumpulan rumus lengkap awalnya diturunkan untuk sembilan belas tipe cluster. Dalam manuskrip ini, kami memperoleh formula ajaib untuk tiga belas jenis nanobox.
Dalam rumus ajaib di bawah ini, kami menemukan bahwa koordinasi massal mungkin muncul untuk t = 2 atau t = 3 lapisan ketebalan cangkang. Sebagian besar untuk lapisan di mana t = 2; pengecualian adalah kubus fcc, kuboctahedron, icosahedron, dan kubus bcc dan kubus terpotong. Dalam yang terakhir, koordinasi massal hanya muncul untuk t = 3 lapisan. Untuk data di bawah ini, tabel formula ajaib disertai dengan sosok 'setengah kotak' untuk menunjukkan interior nanobox. Di sampingnya ada bilah warna yang menunjukkan koordinasi dan jumlah dalam tanda kurung.
Untuk menggambarkan penerapan formula ajaib, kami menguraikan bagaimana perilaku katalitik dapat bergantung pada koordinasi dan formula semacam itu. Kami mendefinisikan G sebagai energi Gibbs tergantung ukuran cluster. Karena adatom yang terikat pada atom kulit terluar, terjadi peningkatan G yang disebut energi adsorpsi dan dilambangkan sebagai \(\Delta G\). Ini dapat dibagi atas berbagai jenis koordinasi atom pada ikatan kulit terluar ke adatom. Sebagai contoh, atom kink menambah energi adsorpsi dengan jumlah \(\Delta G_{k}\). Demikian pula atom sisi menambahkan \(\Delta G_{e}\), sedangkan atom segi memberikan kontribusi \(\Delta G_f\) maka [18]:
$$\Delta G=\sum _{o\in \{f,e,k\}} \Delta G_o N_o$$ (7)di mana \(N_o\) adalah jumlah atom di kulit terluar dari jenis yang ditunjukkan. Jumlah total atom pada kulit terluar yang terikat pada adatom didefinisikan sebagai \(N_s=N_f+N_e+N_k\), menghasilkan:
$$\begin{aligned}\Delta G=&{} \Delta G_f\cdot (1-f_e-f_k)+\Delta G_e\cdot f_e+\Delta G_k\cdot f_k \\&\quad {\hbox{where} } \,\,f_o=N_o/N_s, \,\,o\in \{e,k\},\end{aligned}$$ (8)dengan fraksi energi Gibbs yang diekspresikan melalui tepi dan situs ketegaran yang memiliki koordinasi eksplisit untuk struktur tertentu. Ini menunjukkan bahwa formula ajaib memiliki peran dalam reaksi permukaan, melalui koordinasi tepi dan ketegaran serta formulanya. Perhatikan bahwa Persamaan. (8) berlaku untuk adsorpsi ke situs di atas, jika tidak, tidak semua adatom akan terikat pada atom di kulit terluar. Dalam model seperti itu, situs kink memiliki formula ajaib yang konstan dengan jumlah cangkang, n , situs tepi memiliki rumus yang linier dengan n , dan situs faset memiliki rumus kuadrat dengan n . Lebih khusus lagi, situs kink adalah formula terkoordinasi terendah, situs tepi adalah koordinat terendah kedua, dan situs faset memiliki cn = 8 untuk (100) faset dan cn = 9 untuk (111) faset.
Dua hubungan mendasar pada basis per-partikel dapat diterapkan. Untuk energi Gibbs dan konstanta adsorpsi, \(K_{{\rm a}}\), berlaku:
$$K_{{\rm a}}={\exp } \left( -\frac{\Delta G}{RT}\kanan) ,$$ (9)dimana R adalah konstanta gas dan T adalah suhu dalam Kelvin. Selain itu, hubungan Brønsted–Evans–Polanyi banyak digunakan dalam katalisis homogen dan heterogen [18, 22] menggunakan hubungan untuk konstanta reaksi k dan konstanta kesetimbangan K sebagai berikut:
$$k=gK^{\alpha },\quad 0<\alpha <1,$$ (10)dimana g dan \(\alpha\) (parameter Polanyi) adalah konstanta. Parameter Polanyi tidak memiliki satuan dan merupakan pecahan wajar, seperti yang diberikan oleh Brønsted [23]. Kami kemudian memiliki:
$$k=k'_{a}{\exp } \Bigl (-\alpha \bigl ({f_n^{e}\cdot \chi _{_e}({D_n}) +f_n^{k}\cdot \chi _{_k}({D_n})}\bigr )\Bigr ),$$ (11)dimana
$$\begin{aligned} &\chi _{_e}(D)=\frac{\Delta G_e(D)-\Delta G_f(D)}{RT},\\&\chi _{_k}(D )=\frac{\Delta G_k(D)-\Delta G_f(D)}{RT}, \end{aligned}$$ (12)dan
$$k'_{a}=g\exp \left( -\alpha \frac{\Delta G_f}{RT}\kanan) .$$ (13)Analisis ini menunjukkan bahwa penentuan model katalitik memerlukan metode penghitungan energi Gibbs. Reaksi katalitik yang diketahui seperti mekanisme dua langkah dan mekanisme Langmuir-Hinshelwood telah dipertimbangkan [24].
Struktur kubik berpusat muka adalah bentuk paling umum untuk nanocluster dan nanobox. Ini adalah struktur logam dengan sifat menarik, seperti logam mulia dengan sifat plasmonik, dan logam mulia katalitik. Karena emas memiliki potensi reduksi tinggi 1,50 V (lihat Persamaan 1) dibandingkan dengan elektroda hidrogen standar (SHE) [5], emas adalah salah satu logam termudah untuk disintesis sebagai nanobox atau nanocage. Nanobox emas atau nanocage telah dibentuk dalam bentuk kubik [1], cuboctahedron [25], icosahedron dan decahedron [26], octahedron [27] dan tetrahedron [28].
Kita dapat menentukan perkiraan ukuran nanobox ini dengan menggunakan pendekatan koordinasi untuk panjang ikatan tetangga terdekat r (cn) [29],
$$r(cn) =\frac{2r_{{\rm B}}}{\left( 1+\exp \left( \frac{12 - \langle cn \rangle _c)}{8\cdot \langle cn \rangle _c}\kanan) \kanan) }.$$ (14)Di sini \(r_{{\rm B}}\) adalah panjang ikatan massal untuk emas (0,2884 nm) dan \(\langle cn \rangle _c\) adalah koordinasi rata-rata gugus. Kami menemukan hubungan linier antara D dan n , jumlah shell cluster, seperti yang ditunjukkan pada Tabel 1:
$$D(n)=a \cdot r_{{\rm B}} \cdot n + b.$$ (15)Kami menggunakan nanobox dengan t = 3, karena rumusnya berbeda dengan t , dan kami ingin mencapai beberapa koordinasi massal. Untuk perhitungan D (n ), kami menggunakan jarak maksimum antar atom dalam cluster, yang diturunkan dari matriks Euclidean. Perhatikan bahwa D (n ) adalah rumus empiris, diturunkan dari data (bervariasi n dan hitung D ), dan karena itu tidak terbukti.
Hubungan ini menghasilkan diameter yang sesuai dengan data lain, dari DFT. Untuk kuboctahedra padat dengan N sama dengan 55, 561, dan 923 kita mendapatkan diameter 1,12 nm, 2,85 nm, dan 3,43 nm. Ini lebih baik dibandingkan dengan hasil DFT yang dipublikasikan untuk 55 atom 1,1 nm [30], untuk 561 atom, 2,7 nm [31], dan untuk 923 atom, 3,5 nm [30]. Rumus ajaib untuk beberapa nanobox fcc ditabulasikan di bawah ini (Tabel 2, 3, 4, 5, 6, 7, 8).
Lihat Tabel 9 dan 10.
Struktur kisi kubik berlian dibentuk oleh alotrop karbon serta unsur silikon dan germanium. Juga, beberapa senyawa kubik membentuk struktur ini, seperti oksida besi kubik, maghemite berlian tetrahedral \(\gamma\)-Fe2 O3 . Panjang ikatan Fe–O pada intan tetrahedral maghemite \(\gamma\)-Fe2 O3 = 0,186 nm [32]. Ini mengarah ke diameter kelompok berlian D (n ) seperti di bawah ini:
$$D(n) =3,3984\cdot n_{{\rm B}} \cdot n - 0,21194.$$ (16)Menurut referensi [12], mikroboks oksida besi kubik terbentuk dan memiliki kemampuan penyimpanan lithium yang menarik. Kami tidak mengetahui model koordinasi lengkap untuk penyimpanan energi, tetapi seperti yang disebutkan di atas, hasil DFT menunjukkan bahwa aktivitas mungkin bergantung pada orientasi faset [19]. Tidak ada model ketergantungan penyimpanan pada koordinasi saat ini seperti yang kita miliki untuk katalisis. Dari persamaan (16) di atas (dibuat menggunakan t = 4), microbox membutuhkan sekitar n = 1600 cangkang untuk berlian maghemite. Rumus ajaib untuk berlian dan struktur kisi kubik sederhana tercantum di bawah ini (Tabel 11, 12).
Lihat Tabel 13, 14, dan 15.
Lihat Tabel 16.
Kasus khusus t = 1 unik dan karena itu memiliki formula ajaib yang berbeda. Kami memeriksa kasus ini untuk beberapa kotak nano di atas. Nanobox dengan dinding ultra tipis telah dibentuk dengan bentuk kubik [33], oktahedral [16], dan ikosahedral [34]. Menurut rumus ajaib di bawah ini, kotak nano kubik dengan t = 1 memiliki koordinasi terendah. Platinum memiliki potensi reduksi yang relatif tinggi yaitu 1,18 V dibandingkan SHE, sehingga dapat dibentuk dengan penggantian galvanik, lihat Persamaan. (1) [5]. Namun, sifat reaksi reduksi oksidasi (ORR) dari beberapa nanocage berbasis platinum ini menunjukkan bahwa struktur dengan (111) faset dibandingkan dengan (100) faset memiliki aktivitas massa ORR yang lebih baik [35].
Dengan demikian ikosahedron dengan 20 (111) segi memiliki aktivitas massa ORR terbaik, diikuti oleh segi delapan, dan terakhir kubus terpotong. Sifat perilaku katalitik dari orientasi segi lebih diutamakan daripada bilangan koordinasi dibuktikan oleh data tabular di bawah ini. Dengan kata lain, seperti disebutkan dalam tabel berikut, kubus dengan (100) segi memiliki bilangan koordinasi ajaib terendah dengan empat dan lima, namun oktahedron dan ikosahedron dengan (111) segi dan rumus ajaib yang lebih besar memiliki aktivitas ORR yang lebih baik. Properti ini juga dibuktikan dalam nanocluster, di mana hasil DFT mengkonfirmasi dominasi (111) faset [36], terutama untuk paduan PtNi (Tabel 17, 18, 19, 20, 21).
Mengingat pentingnya situs tepi dan ketegaran relatif terhadap yang segi sehubungan dengan aktivitas katalitik, kami telah menentukan dispersi permukaan untuk beberapa kotak nano yang kami pelajari. (100) faset memiliki cn = 8 sedangkan (111) faset memiliki cn = 9. Hal ini dapat memberikan wawasan tentang alasan aktivitas polihedral individu jika dibandingkan di antara nanobox. Pada Gambar. 1 di bawah, kami memplot dispersi permukaan \(D_{{\rm s}} =(N_{{\rm e}} + N_{{\rm k}}) / N_{{\rm S}} \cdot 100\%\). Dalam hubungan ini \(N_{{\rm k}}\) adalah jumlah situs ketegaran atau sudut dan \(N_{{\rm e}}\) jumlah situs tepi. Seperti dapat dilihat pada Gambar 1, nanobox dengan (111) permukaan yang berlawanan dengan (100) permukaan memiliki dispersi yang lebih tinggi, memberikan kepercayaan pada preferensi aktivitas katalitik dari faset (111).
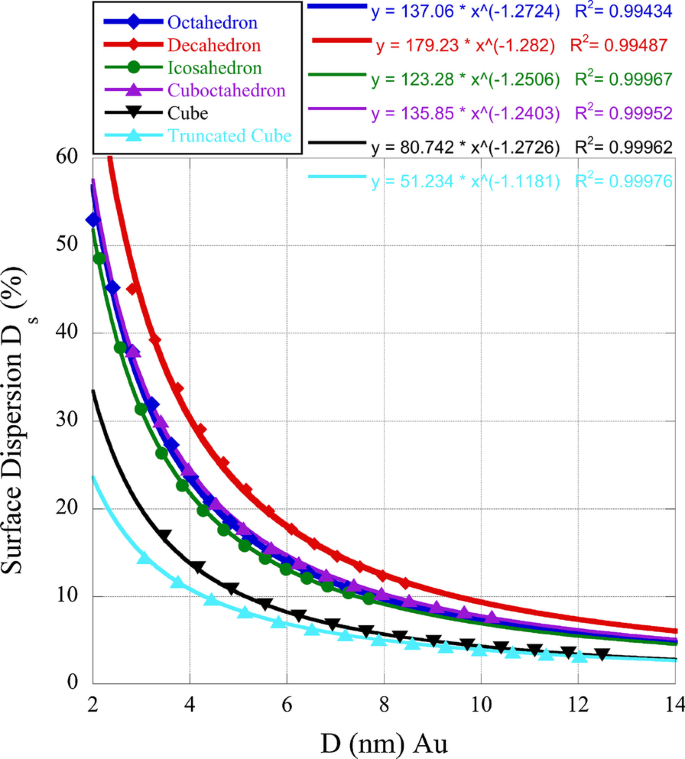
Dispersi permukaan kotak nano emas
Singkatnya, kami telah menyajikan deskripsi matematis terperinci pertama tentang formula ajaib untuk kotak nano. Kasus ketebalan cangkang, t = 1 berbeda dari \(t>1\) dan kami mentabulasi data untuk beberapa kasus ini. Rumus untuk koordinasi, jumlah atom, dan jumlah ikatan semuanya disebutkan. Kami menemukan bahwa koordinasi massal muncul untuk lapisan di mana t = 2 atau 3, dan karenanya jauh lebih tipis daripada yang disintesis secara normal. Manfaat koordinasi rendah hanya dicapai untuk dinding yang sangat tipis. Kami berharap hasil ini berguna untuk pemodelan dan pekerjaan eksperimental.
Kumpulan data yang mendukung kesimpulan artikel ini dapat diperoleh dari penulis terkait.
Kubus berpusat badan
Kubus berpusat muka
Kemasan tutup heksagonal
Teori fungsi densitas
Elektroda hidrogen sekunder
bahan nano
Abstrak Ukuran dan sifat permukaan seperti katalisis, optical quantum dot photoluminescense, dan resonansi plasmon permukaan bergantung pada koordinasi dan kimia logam dan nanocluster semikonduktor. Sifat yang bergantung pada koordinasi tersebut dikuantifikasi di sini melalui rumus ajaib untuk juml
Abstrak Ozon konsentrasi tinggi dapat sangat merusak sistem pernapasan, kardiovaskular, dan kesuburan manusia, dan dekomposisi katalitik merupakan strategi penting untuk mengurangi bahayanya. Namun, tetap menjadi tantangan untuk mengembangkan katalis dekomposisi ozon yang efisien dengan efisiensi t
Abstrak Terlepas dari beberapa upaya, pengembangan vaksin yang efektif untuk COVID-19 mungkin membutuhkan waktu lebih lama. Pengobatan tradisional/alami yang sudah dialami manusia bisa menjadi solusi lebih awal. Mempertimbangkan pengalaman tim peneliti dalam menggunakan nano-clays sebagai bahan afi
Sebuah for loop adalah loop yang paling banyak digunakan dalam perangkat lunak, tetapi terutama digunakan untuk mereplikasi logika perangkat keras di Verilog. Ide di balik for loop adalah untuk mengulangi satu set pernyataan yang diberikan dalam loop selama kondisi yang diberikan benar. Ini sangat m
