Identitas Aljabar Boolean

Dalam matematika, sebuah identitas adalah pernyataan yang benar untuk semua nilai yang mungkin dari variabel atau variabelnya.

Identitas aljabar x + 0 =x memberi tahu kita bahwa segala sesuatu (x) ditambahkan ke nol sama dengan "apa saja" yang asli, tidak peduli berapa nilainya bahwa "apa pun ” (x) mungkin.

Seperti aljabar biasa, aljabar Boolean memiliki identitas uniknya sendiri berdasarkan keadaan bivalen variabel Boolean.

Identitas Tambahan

Menambahkan Nol

Identitas Boolean pertama adalah jumlah dari apapun dan nol sama dengan “apa saja . yang asli .”

Identitas ini tidak berbeda dengan persamaan aljabar bilangan real:

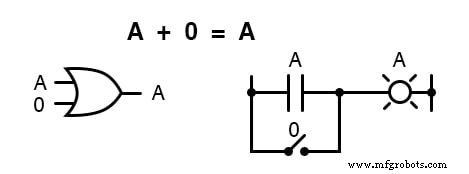
Berapapun nilai A , hasilnya akan selalu sama:ketika A=1 , outputnya juga akan menjadi 1; ketika A=0 , outputnya juga akan menjadi 0 .

Menambahkan Satu

Identitas berikutnya jelas berbeda dari yang terlihat dalam aljabar normal.

Di sini kita menemukan bahwa jumlah dari “apapun ” dan satu adalah satu :

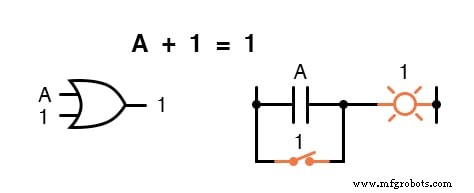
Berapapun nilai A, jumlah A dan 1 akan selalu 1.

Dalam arti tertentu, sinyal “1” menggantikan efek A pada rangkaian logika, membiarkan output tetap pada level logika 1.

Menambahkan Kuantitas ke Dirinya Sendiri

Selanjutnya, kami menguji pengaruh penambahan A dan A bersama-sama, yang sama dengan menghubungkan kedua input dari gerbang OR satu sama lain dan mengaktifkannya dengan sinyal yang sama:

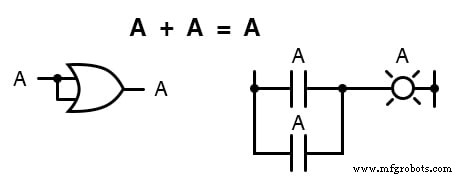
Dalam aljabar bilangan real, jumlah dua variabel identik adalah dua kali nilai variabel aslinya (x + x =2 x), tetapi ingat bahwa tidak ada konsep “2” di dunia matematika Boolean, hanya 1 dan 0, jadi kita tidak dapat mengatakan bahwa A + A =2A .

Jadi, ketika kita menambahkan kuantitas Boolean ke dirinya sendiri, jumlahnya sama dengan kuantitas aslinya:0 + 0 =0 , dan 1 + 1 =1 .

Menambahkan Kuantitas ke Pelengkapnya

Memperkenalkan konsep komplementer Boolean yang unik ke dalam identitas aditif, kami menemukan efek yang menarik.

Karena harus ada satu “1 ” nilai antara variabel apa pun dan komplemennya, dan karena jumlah setiap kuantitas Boolean dan 1 adalah 1, jumlah variabel dan komplemennya harus 1:

Identitas Perkalian

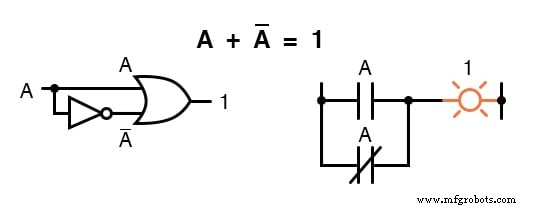
Sama seperti ada empat identitas aditif Boolean (A+0, A+1, A+A, dan A+A’ ), jadi ada juga empat identitas perkalian:Ax0, Ax1, AxA, dan AxA’ . Dari jumlah tersebut, dua yang pertama tidak berbeda dari ekspresi yang setara dalam aljabar reguler:

Dikalikan dengan 0 atau 1

Mengkalikan Besaran dengan Sendirinya

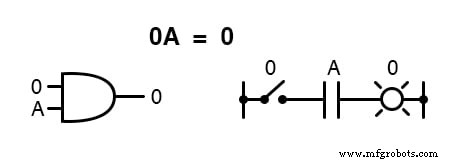
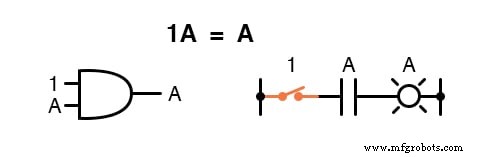
Identitas perkalian ketiga menyatakan hasil dari kuantitas Boolean dikalikan dengan dirinya sendiri.

Dalam aljabar normal, hasil kali variabel dan variabel itu sendiri adalah persegi dari variabel tersebut (3 x 3 =3 ² =9).

Namun, konsep persegi menyiratkan jumlah 2, yang tidak memiliki arti dalam aljabar Boolean, jadi kita tidak dapat mengatakan bahwa A x A =A ² .

Sebagai gantinya, kami menemukan bahwa produk dari kuantitas Boolean dan dirinya sendiri adalah kuantitas asli, karena 0 x 0 =0 dan 1 x 1 =1 :

Mengkalikan Besaran dengan Pelengkapnya

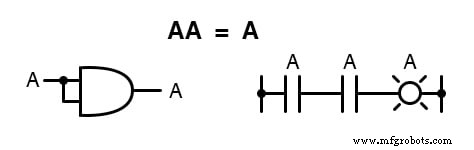
Identitas perkalian keempat tidak memiliki padanan dalam aljabar reguler karena menggunakan komplemen dari variabel, sebuah konsep yang unik untuk matematika Boolean.

Karena harus ada satu “0 ” nilai antara variabel apa pun dan pelengkapnya, dan karena produk dari setiap kuantitas Boolean dan 0 adalah 0 , hasil kali variabel dan komplemennya harus 0 :

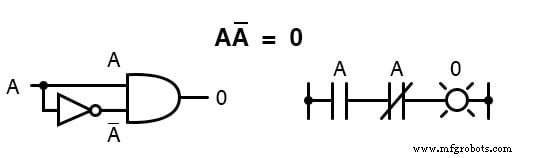
Untuk meringkasnya, kita memiliki empat identitas Boolean dasar untuk penjumlahan dan empat untuk perkalian:

Pelengkap Ganda

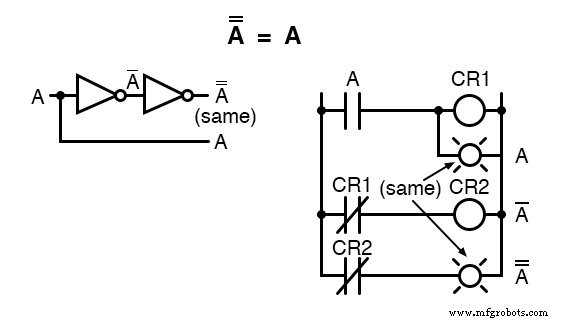
Identitas lain yang berkaitan dengan komplementasi adalah pelengkap ganda :variabel dibalik dua kali.

Melengkapi variabel dua kali (atau beberapa kali genap) menghasilkan nilai Boolean asli.

Ini analog dengan meniadakan (dikalikan dengan -1) dalam aljabar bilangan real:jumlah negasi genap dibatalkan untuk meninggalkan nilai aslinya:

LEMBAR KERJA TERKAIT:

• Lembar Kerja Aljabar Boolean