Mesin Keadaan Hingga

Hingga saat ini, setiap sirkuit yang ditampilkan adalah kombinatorial sirkuit. Itu berarti bahwa outputnya hanya bergantung pada inputnya saat ini. Input sebelumnya untuk jenis sirkuit tersebut tidak berpengaruh pada output.

Namun, ada banyak aplikasi di mana ada kebutuhan sirkuit kita untuk memiliki "memori"; untuk mengingat input sebelumnya dan menghitung output mereka sesuai dengan mereka. Sirkuit yang outputnya tidak hanya bergantung pada input saat ini tetapi juga pada riwayat input disebut sirkuit berurutan .

Pada bagian ini kita akan belajar bagaimana merancang dan membangun rangkaian sekuensial tersebut. Untuk melihat bagaimana prosedur ini bekerja, kita akan menggunakan sebuah contoh, di mana kita akan mempelajari topik kita.

Jadi, misalkan kita memiliki permainan kuis digital yang bekerja pada jam dan membaca input dari tombol manual. Namun, kami ingin sakelar hanya mengirimkan satu pulsa TINGGI ke sirkuit. Jika kita mengaitkan tombol secara langsung pada sirkuit permainan, itu akan mengirimkan TINGGI selama beberapa siklus jam yang dapat dicapai oleh jari kita. Pada frekuensi jam yang umum, jari kita tidak akan pernah cukup cepat.

Prosedur desain memiliki langkah-langkah khusus yang harus diikuti untuk menyelesaikan pekerjaan:

Langkah 1

Langkah pertama dari prosedur desain adalah mendefinisikan dengan kata-kata sederhana namun jelas apa yang kita ingin sirkuit kita lakukan:

“Misi kami adalah merancang sirkuit sekunder yang akan mengirimkan pulsa TINGGI dengan durasi hanya satu siklus ketika tombol manual ditekan, dan tidak akan mengirimkan pulsa lain sampai tombol ditekan dan ditekan lagi.”

Langkah 2

Langkah selanjutnya adalah mendesain State Diagram.

Ini adalah diagram yang dibuat dari lingkaran dan panah dan menggambarkan secara visual pengoperasian sirkuit kami. Dalam istilah matematika, diagram yang menggambarkan operasi rangkaian sekuensial ini adalah Mesin Keadaan Hingga. Catat bahwa ini adalah Moore Finite State Machine.

Outputnya adalah fungsi hanya dari keadaan saat ini, bukan inputnya. Berbeda dengan Mealy Finite State Machine, dimana input mempengaruhi output. Dalam tutorial ini, hanya Moore Finite State Machine yang akan diperiksa.

Diagram Status dari sirkuit kami adalah sebagai berikut:(Gambar di bawah)

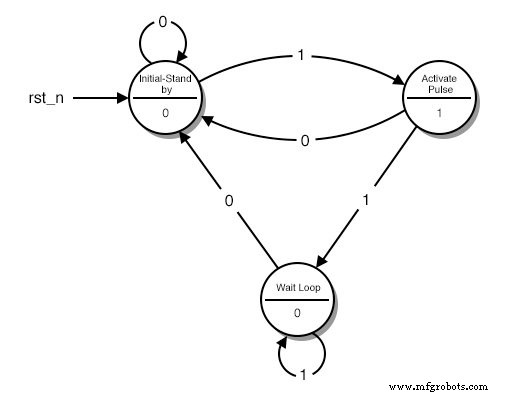
Diagram Keadaan

Setiap lingkaran mewakili "keadaan", kondisi yang didefinisikan dengan baik di mana mesin kami dapat ditemukan. Di bagian atas lingkaran kami menggambarkan kondisi itu. Deskripsi membantu kita mengingat apa yang seharusnya dilakukan sirkuit kita pada kondisi itu.

• Lingkaran pertama adalah kondisi "siaga". Di sinilah sirkuit kami dimulai dan menunggu tombol lain ditekan.
• Lingkaran kedua adalah kondisi tombol baru saja ditekan dan rangkaian kita perlu mengirimkan pulsa TINGGI.
• Lingkaran ketiga adalah kondisi dimana sirkuit kita menunggu tombol dilepas sebelum kembali ke kondisi “stand-by”.

Di bagian bawah lingkaran adalah output dari rangkaian kami. Jika kita ingin sirkuit kita mentransmisikan TINGGI pada keadaan tertentu, kita menempatkan 1 pada keadaan itu. Jika tidak, kita beri 0.

Setiap panah mewakili "transisi" dari satu keadaan ke keadaan lain. Transisi terjadi sekali setiap siklus clock. Tergantung pada Input saat ini, kita dapat pergi ke keadaan yang berbeda setiap kali. Perhatikan nomor di tengah setiap panah. Ini adalah Input saat ini.

Misalnya, ketika kita berada dalam status "Initial-Stand by" dan kita "membaca" angka 1, diagram memberitahu kita bahwa kita harus pergi ke status "Activate Pulse". Jika kita membaca 0 kita harus tetap dalam status “Initial-Stand by”.

Jadi, apa sebenarnya yang dilakukan "Mesin" kita? Itu dimulai dari status "Initial - Stand by" dan menunggu sampai 1 dibaca di Input. Kemudian ia beralih ke status "Aktifkan Pulsa" dan mengirimkan pulsa TINGGI pada outputnya. Jika tombol terus ditekan, sirkuit beralih ke status ketiga, "Loop Tunggu".

Di sana ia menunggu hingga tombol dilepaskan (Input menjadi 0) sambil mengirimkan LOW pada output. Kemudian semuanya akan berakhir lagi!

Ini mungkin bagian yang paling sulit dari prosedur desain, karena tidak dapat dijelaskan dengan langkah-langkah sederhana. Dibutuhkan pengalaman dan sedikit pemikiran yang tajam untuk membuat Diagram Keadaan, tetapi sisanya hanyalah serangkaian langkah yang telah ditentukan.

Langkah 3

Selanjutnya, kami mengganti kata-kata yang menggambarkan status diagram yang berbeda dengan biner angka. Kami memulai pencacahan dari 0 yang ditugaskan pada keadaan awal. Kami kemudian melanjutkan pencacahan dengan negara bagian mana pun yang kami suka, sampai semua negara bagian memiliki nomornya. Hasilnya terlihat seperti ini:(Gambar di bawah)

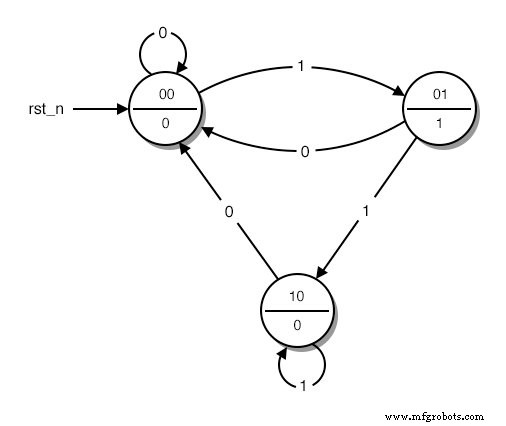
Diagram Status dengan Kode Status

Langkah 4

Setelah itu, kita isi Tabel Negara . Tabel ini memiliki bentuk yang sangat spesifik. Saya akan memberikan tabel contoh kita dan menggunakannya untuk menjelaskan cara mengisinya. (Gambar di bawah)

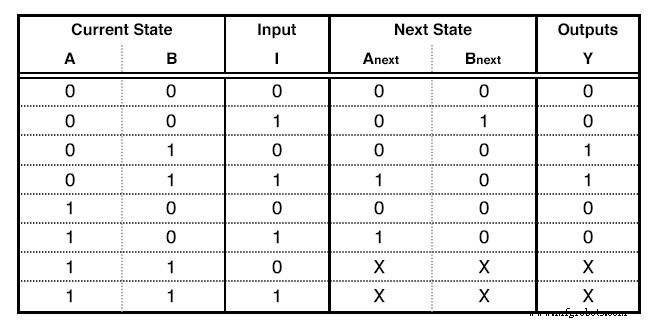
Tabel Status

Kolom pertama adalah sebanyak bit dari angka tertinggi yang kami tetapkan Diagram Negara. Jika kami memiliki 5 negara bagian, kami akan menggunakan hingga angka 100, yang berarti kami akan menggunakan 3 kolom. Untuk contoh kita, kita menggunakan hingga angka 10, jadi hanya dibutuhkan 2 kolom. Kolom ini menjelaskan Status Saat Ini dari sirkuit kami.

Di sebelah kanan kolom Status Saat Ini kami menulis Kolom Input . Ini akan menjadi sebanyak variabel Input kami. Contoh kita hanya memiliki satu Input.

Selanjutnya, kita tulis Kolom Status Berikutnya . Ini adalah sebanyak kolom Status Saat Ini.

Akhirnya, kami menulis Kolom Keluaran . Ini adalah sebanyak output kami. Contoh kita hanya memiliki satu output. Karena kami telah membangun Mesin Keadaan Lebih Hingga, keluarannya hanya bergantung pada keadaan masukan saat ini. Inilah alasan mengapa kolom keluaran memiliki dua 1:untuk menghasilkan fungsi Boolean keluaran yang tidak bergantung pada masukan I. Teruskan membaca untuk detail lebih lanjut. Kolom Current State dan Input adalah Input dari tabel kita. Kami mengisinya dengan semua angka biner dari 0 hingga:

2 ^{(Jumlah kolom Status Saat Ini + Jumlah kolom Input)} -1

Ini lebih sederhana daripada kedengarannya untungnya. Biasanya akan ada lebih banyak baris daripada Status sebenarnya yang telah kita buat di Diagram Status, tapi tidak apa-apa.

Setiap baris dari kolom Next State diisi sebagai berikut:Kita mengisinya dengan state yang kita capai ketika, dalam State Diagram, dari Current State dari baris yang sama kita mengikuti Input dari baris yang sama. Jika harus mengisi baris yang nomor Status Saat Ini tidak sesuai dengan Status sebenarnya pada Diagram Status, kami mengisinya dengan istilah Tidak Peduli (X). Lagi pula, kita tidak peduli ke mana kita bisa pergi dari Negara yang tidak ada. Kami tidak akan berada di sana sejak awal! Sekali lagi ini lebih sederhana daripada kedengarannya.

Kolom keluaran diisi oleh keluaran dari Status Saat Ini yang sesuai dalam Diagram Status.

Tabel Negara selesai! Ini menggambarkan perilaku sirkuit kita sepenuhnya seperti Diagram Keadaan.

Langkah 5a

Langkah selanjutnya adalah mengambil "Mesin" teoretis itu dan mengimplementasikannya dalam sebuah rangkaian. Paling sering, implementasi ini melibatkan Flip Flops. Panduan ini didedikasikan untuk implementasi semacam ini dan akan menjelaskan prosedur untuk D - Flip Flops maupun JK - Flip Flops. T - Flip Flops tidak akan disertakan karena terlalu mirip dengan dua kasus sebelumnya. Pemilihan Flip Flop yang akan digunakan bersifat sewenang-wenang dan biasanya ditentukan oleh faktor biaya. Pilihan terbaik adalah melakukan kedua analisis dan memutuskan jenis Flip Flop mana yang menghasilkan jumlah gerbang logika minimum dan biaya lebih rendah.

Pertama kita akan memeriksa bagaimana kita mengimplementasikan “Mesin” kita dengan D-Flip Flops.

Kita akan membutuhkan D - Flip Flops sebanyak kolom State, 2 dalam contoh kita. Untuk setiap Flip Flop kami akan menambahkan satu kolom lagi di tabel State kami (Gambar di bawah) dengan nama input Flip Flop, "D" untuk kasus ini. Kolom yang sesuai dengan masing-masing Flip Flop menjelaskan input apa yang harus kita berikan pada Flip Flop untuk berpindah dari Status Saat Ini ke Status Berikutnya . Untuk D - Flip Flop ini mudah:Input yang diperlukan sama dengan Status Berikutnya. Di baris yang berisi X, kami juga mengisi X di kolom ini.

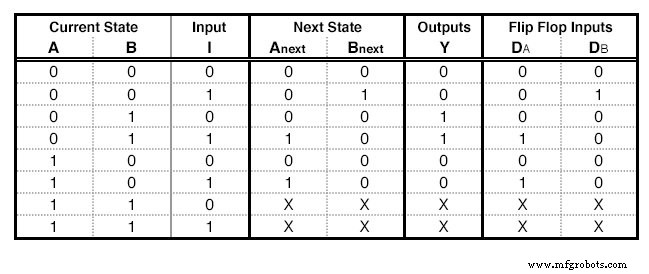
Tabel Status dengan D - Eksitasi Flip Flop

Langkah 5b

Kita bisa melakukan langkah yang sama dengan JK - Flip Flops. Namun ada beberapa perbedaan. A JK - Flip Flop memiliki dua input, oleh karena itu kita perlu menambahkan dua kolom untuk setiap Flip Flop. Isi setiap sel ditentukan oleh tabel eksitasi JK:

Tabel ini mengatakan bahwa jika kita ingin pergi dari Negara Q ke Negara Q_berikutnya , kita perlu menggunakan input khusus untuk setiap terminal. Misalnya, untuk beralih dari 0 ke 1, kita perlu memberi makan J dengan 1 dan kita tidak peduli input mana yang kita masukkan ke terminal K.

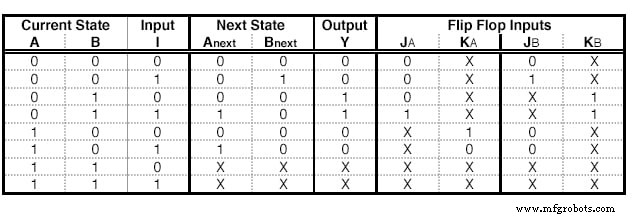
Tabel Status dengan JK - Eksitasi Flip Flop

Langkah 6

Kami berada di tahap akhir dari prosedur kami. Yang tersisa, adalah menentukan fungsi Boolean yang menghasilkan input dari Flip Flops dan Output kita. Kami akan mengekstrak satu fungsi Boolean untuk setiap input Flip Flop yang kami miliki. Ini dapat dilakukan dengan Peta Karnaugh. Variabel input peta ini adalah variabel Status Saat Ini dan juga Masukan.

Dengan demikian, fungsi input untuk D - Flip Flops kami adalah sebagai berikut:(Gambar di bawah)

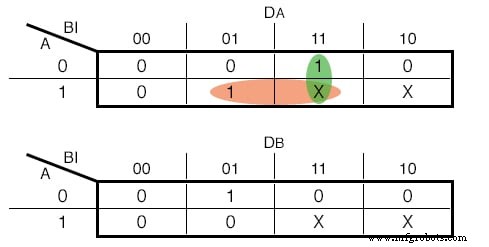
Karnaugh Maps untuk D - Input Flip Flop

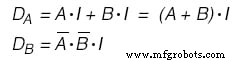
Jika kami memilih untuk menggunakan JK - Flip Flops, fungsi kami adalah sebagai berikut:(Gambar di bawah)

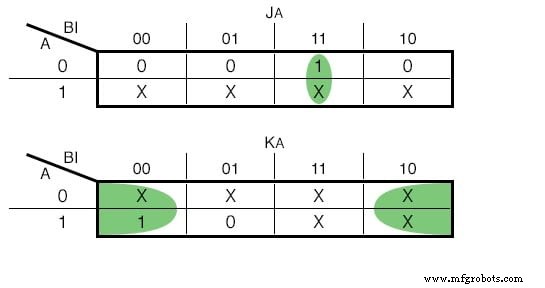
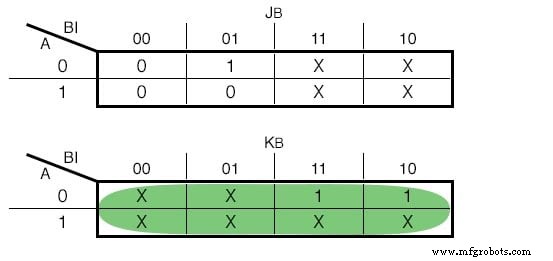
Peta Karnaugh untuk JK - Masukan Flip Flop

Peta Karnaugh akan digunakan untuk menentukan fungsi Output juga:(Gambar di bawah)

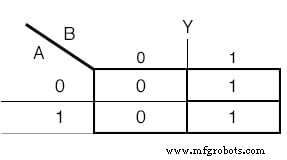
Peta Karnaugh untuk variabel Output Y

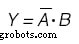
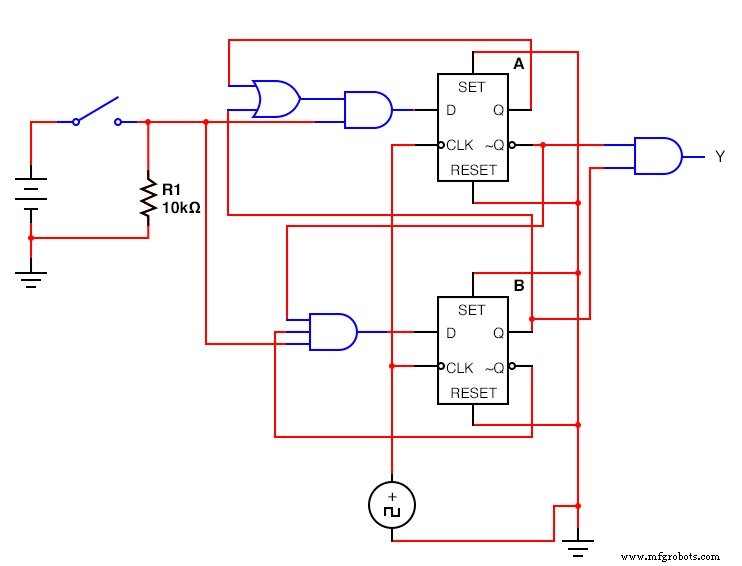
Langkah 7

Kami merancang sirkuit kami. Kami menempatkan Flip Flops dan menggunakan gerbang logika untuk membentuk fungsi Boolean yang kami hitung. Gerbang mengambil input dari output Flip Flops dan Input dari rangkaian. Jangan lupa hubungkan jam ke Flip Flops!

Versi D - Flip Flop:(Gambar di bawah)

Sirkuit Sekuensial D - Flip Flop yang telah selesai

Versi JK - Flip Flop:(Gambar di bawah)

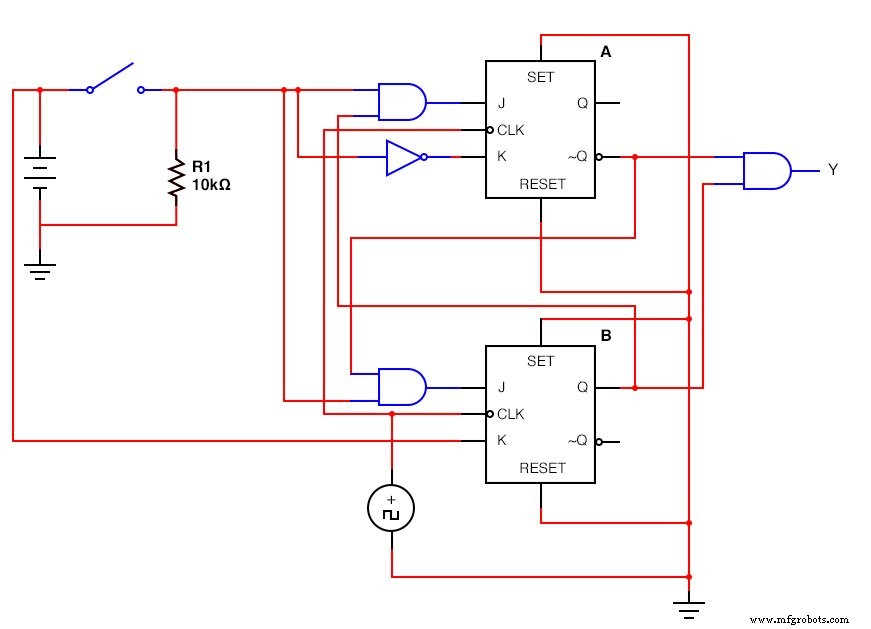
JK - Sirkuit Sekuensial Flip Flop yang telah selesai

Ini dia! Kami telah berhasil merancang dan membangun Sirkuit Sekuensial. Pada awalnya mungkin tampak tugas yang menakutkan, tetapi setelah latihan dan pengulangan prosedur akan menjadi sepele. Sirkuit Sekuensial dapat berguna sebagai bagian kontrol dari sirkuit yang lebih besar dan dapat melakukan tugas logika sekuensial apa pun yang dapat kita pikirkan. Langit adalah batasnya! (atau setidaknya papan sirkuit)

TINJAUAN:

• Fungsi Logika Sekuensial memiliki fitur "memori" dan memperhitungkan masukan sebelumnya untuk memutuskan keluaran.
• Mesin Keadaan Hingga adalah model matematika abstrak dari fungsi logika sekuensial. Ini memiliki input, output, dan jumlah status yang terbatas.
• FSM diimplementasikan di sirkuit kehidupan nyata melalui penggunaan Flip Flops
• Prosedur implementasi memerlukan urutan langkah (algoritma) tertentu agar dapat dijalankan.