19 Unit 2:Alat Mesin CNC Sumbu yang Dapat Diprogram dan Sistem Dimensi Posisi
TUJUAN
Setelah menyelesaikan unit ini, Anda seharusnya dapat:
- Memahami sistem koordinat kartesius.
- Pahami koordinat Cartesian pesawat.
- Memahami koordinat Cartesian ruang tiga dimensi.
- Pahami empat Kuadran.
- Jelaskan perbedaan koordinat kutub dan persegi panjang.
- Identifikasi sumbu yang dapat diprogram pada mesin CNC.
SISTEM KOORDINAT KARTESIAN
Koordinat kartesius memungkinkan seseorang untuk menentukan lokasi suatu titik pada bidang, atau dalam ruang tiga dimensi. Koordinat Cartesian atau sistem koordinat persegi panjang dari suatu titik adalah sepasang angka (dalam dua dimensi) atau triplet angka (dalam tiga dimensi) yang menentukan jarak bertanda dari sumbu koordinat. Pertama kita harus memahami sistem koordinat untuk menentukan arah dan posisi relatif kita. Sistem yang digunakan untuk menentukan titik dalam ruang dengan menetapkan arah (sumbu) dan posisi referensi (asal). Sistem koordinat dapat berbentuk persegi panjang atau kutub.
Sebagaimana titik-titik pada garis dapat ditempatkan dalam korespondensi satu-satu dengan garis bilangan real, demikian pula titik-titik pada bidang dapat ditempatkan dalam korespondensi satu-satu dengan pasangan garis bilangan real dengan menggunakan dua garis koordinat. Untuk melakukan ini, kami membangun dua garis koordinat tegak lurus yang berpotongan di titik asalnya; untuk kenyamanan. Tetapkan satu set gradasi ruang yang sama ke sumbu x dan y mulai dari titik asal dan menuju ke dua arah, titik kiri dan kanan (sumbu x) dan atas dan bawah (sumbu y) sepanjang setiap sumbu dapat ditetapkan. Kami membuat salah satu garis bilangan vertikal dengan arah positif ke atas dan arah negatif ke bawah. Garis bilangan lainnya mendatar dengan arah positif ke kanan dan arah negatif ke kiri. Dua garis bilangan disebut sumbu koordinat; garis horizontal adalah sumbu x, garis vertikal adalah sumbu y, dan sumbu koordinat bersama-sama membentuk sistem koordinat Cartesian atau sistem koordinat persegi panjang. Titik potong sumbu koordinat dilambangkan dengan O dan merupakan titik asal sistem koordinat. Lihat Gambar 1.
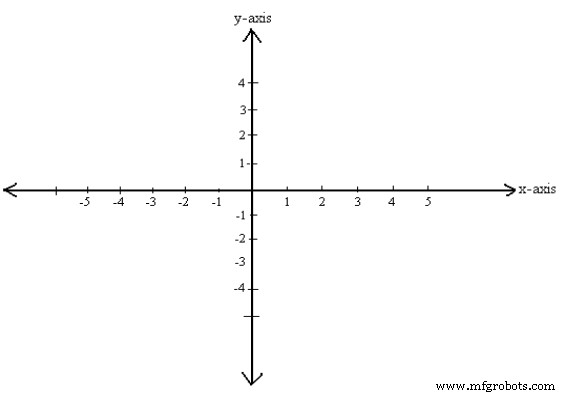
Gambar 1
Pada dasarnya, Dua Garis Bilangan Nyata Disatukan, satu ke kiri-kanan, dan yang lainnya naik-turun. Garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y.
Asal usul
Titik (0,0) diberi nama khusus “The Origin”, dan terkadang diberi huruf “O”.
Garis Bilangan Nyata
Dasar dari sistem ini adalah garis bilangan real yang ditandai pada interval yang sama. Sumbu diberi label (X, Y atau Z). Satu titik pada garis ditetapkan sebagai Asal. Angka-angka di satu sisi garis ditandai sebagai positif dan angka-angka di sisi lain ditandai negatif. Lihat Gambar 2.
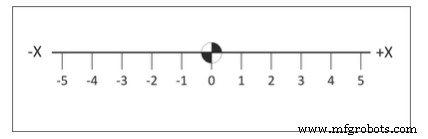
Gambar 2. Garis bilangan sumbu X
Koordinat Cartesian bidang
Sebuah bidang di mana sistem koordinat persegi panjang telah diperkenalkan adalah bidang koordinat atau bidang xy. Kami sekarang akan menunjukkan bagaimana membangun korespondensi satu-satu antara titik-titik dalam bidang koordinat dan pasangan bilangan real. Jika A adalah titik pada bidang koordinat, maka kita menggambar dua garis melalui A, satu tegak lurus terhadap sumbu x dan satu tegak lurus terhadap sumbu y. Jika garis pertama memotong sumbu x di titik dengan koordinat x dan garis kedua memotong sumbu y di titik dengan koordinat y, maka kita kaitkan pasangan (x,y) dengan A( Lihat Gambar 2). Angka a adalah koordinat x atau absis dari P dan angka b adalah koordinat y atau koordinat p; kita katakan bahwa A adalah titik dengan koordinat (x,y) dan dilambangkan dengan A(x,y). Titik (0,0) diberi nama khusus “The Origin”, dan terkadang diberi huruf “O”.
Absis dan Ordinasi:
Kata-kata “Abscissa” dan “Ordinate” … hanyalah nilai-nilai xandy:
- Abscissa:nilai horizontal (“x”) dalam sepasang koordinat:seberapa jauh titik tersebut.
- Ordinate:nilai vertikal (“y”) dalam sepasang koordinat:seberapa jauh titik naik atau turun.
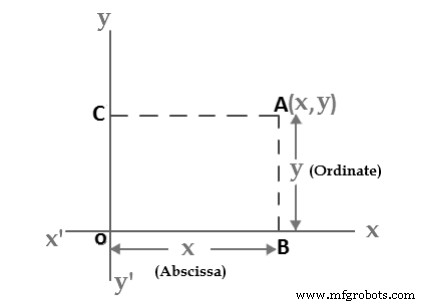
Gambar 3
Nilai Negatif X dan Y:
Garis Bilangan Riil, Anda juga dapat memiliki nilai negatif.
Negatif:mulai dari nol dan menuju ke arah yang berlawanan; Lihat Gambar 4
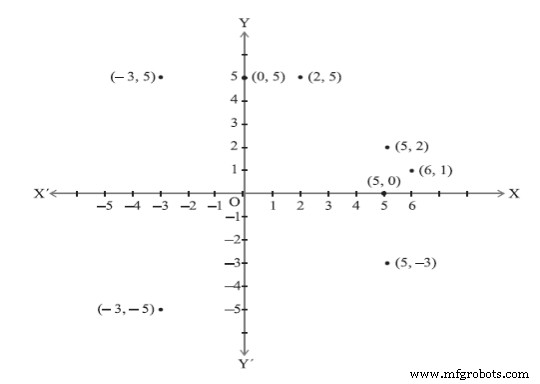
Gambar 4
Jadi, untuk bilangan negatif:
- ke kiri untuk x
- turun untuk y
Misal(-3,5)berarti:
ke kiri sepanjang sumbu x 3 lalu naik 5 pada sumbu y. (Kuadran II x negatif ,y positif)Dan(-3,-5)artinya:
ke kiri sepanjang sumbu x 3 lalu turun 5 pada sumbu y. (Kuadran III x negatif ,y negatif)Dengan menggunakan Koordinat Cartesian, tandai titik pada grafik dengan seberapa jauh dan seberapa jauh ke atas; Lihat gambar 5. Titik (12,5) adalah 12 satuan sepanjang sumbu x, dan 5 satuan di atas sumbu y.
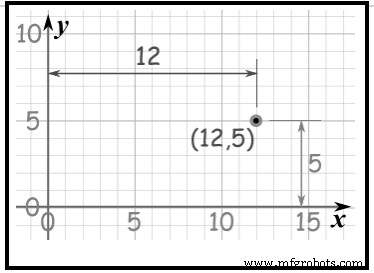
Gambar 5
Sumbu X dan Y: 
Garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y; kedua garis berjalan melalui nol(Asal, (0,0)).

Garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y; kedua garis melewati nol(Asal, (0,0)). Letakkan keduanya pada grafik …Lihat gambar 6
Gambar 6
Ini pada dasarnya, satu set dua baris Bilangan Riil.
Sumbu:Garis referensi dari mana jarak diukur.
Contoh:
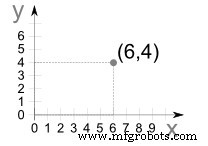
Titik(6,4)adalah
Lanjutkan ke arah x 6 satuan lalu naik 4 satuan ke arah atas lalu “plot titik”.
Dan Anda dapat mengingat sumbu mana dengan:
Koordinat selalu ditulis dalam urutan tertentu:
- jarak horizontal dulu,
- lalu jarak vertikal.
Pasangan yang dipesan:
Angka-angka dipisahkan dengan koma, dan tanda kurung diletakkan di sekelilingnya seperti ini: (7,4)
Contoh:(7,4) berarti 7 satuan ke kanan (sumbu x), dan 4 satuan ke atas (sumbu y)
Koordinat kartesius ruang tiga dimensi
Dalam ruang tiga dimensi (ruang xyz), berorientasi tegak lurus terhadap bidang xy. Sumbu z, melewati titik asal bidang xy. Koordinat ditentukan menurut timur-barat untuk sumbu x utara-selatan untuk sumbu y, dan atas-bawah untuk perpindahan sumbu z dari titik asal. Sistem koordinat kartesius didasarkan pada tiga sumbu koordinat yang saling tegak lurus:sumbu-x, sumbu-mereka, dan sumbu-thez, Lihat Gambar 6 di bawah. Ketiga sumbu tersebut berpotongan pada titik yang disebut titik asal. Anda bisa membayangkan asalnya menjadi titik di mana dinding di sudut ruangan bertemu dengan lantai. Sumbu-x adalah garis horizontal di mana dinding di sebelah kiri Anda dan lantai berpotongan. Sumbu mereka adalah garis horizontal di mana dinding di sebelah kanan Anda dan lantai berpotongan. Sumbu Thez adalah garis vertikal di mana dinding berpotongan. Bagian dari garis yang Anda lihat saat berdiri di dalam ruangan adalah bagian positif dari masing-masing sumbu. Bagian negatif dari sumbu ini adalah kelanjutan dari garis di luar ruangan.
Gambar 7. Sistem Koordinat Kartesius 3D
Sumbu koordinat kartesius tiga dimensi. Representasi dari tiga sumbu sistem koordinat Cartesian tiga dimensi. Sumbu x positif, sumbu positif, dan sumbu z positif adalah sisi-sisi yang diberi label byx,yandz. Asal adalah perpotongan semua sumbu. Cabang setiap sumbu di sisi berlawanan dari titik asal (sisi yang tidak berlabel) adalah bagian negatif.
Ketika berhadapan dengan gerak 3 dimensi, adalah mengatur sistem koordinat yang sesuai. Jenis sistem koordinat yang paling lurus disebut sistem kartesius. Sistem koordinat kartesius terdiri dari tiga sumbu yang saling tegak lurus, yaitu sumbu X, Y, dan Z. Berdasarkan kesepakatan, orientasi sumbu-sumbu ini sedemikian rupa sehingga ketika jari telunjuk, jari tengah, dan ibu jari tangan kanan diatur sedemikian rupa sehingga saling tegak lurus, jari telunjuk, jari tengah, dan ibu jari dapat saling tegak lurus. disejajarkan di sepanjang sumbu X, Y, dan Z, masing-masing. Sistem koordinat seperti itu disebut tangan kanan. Lihat Gambar 7. Titik perpotongan ketiga sumbu koordinat disebut asal usul sistem koordinat.
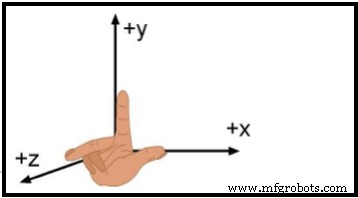
Gambar 8. Sistem Kartesius Tangan Kanan
Koordinat Cartesian dari suatu titik dalam tiga dimensi adalah triplet bilangan (x,y,z). Tiga angka, atau koordinat, masing-masing menentukan jarak bertanda dari titik asal sepanjang sumbu x, y, dan z. Mereka dapat divisualisasikan dengan membentuk kotak dengan tepi sejajar dengan sumbu koordinat dan sudut yang berlawanan pada titik asal dan titik yang diberikan.
Titik-titik sekarang dapat didefinisikan dalam volume ruang tiga dimensi. Hal ini memungkinkan untuk menentukan titik-titik dalam tiga dimensi dari titik asal. Koordinat Cartesian (x,y,z) dari suatu titik dalam tiga dimensi masing-masing menentukan jarak bertanda dari titik asal di sepanjang sumbu x,y, dan z. Titik sumbu Z menjadi entri ketiga saat menentukan lokasi koordinat.
Dengan analogi sudut ruangan di atas, kita dapat membentuk koordinat Cartesian dari titik di atas kepala Anda, sebagai berikut. Bayangkan Anda setinggi lima meter pada sumbu z, dan Anda berjalan dua meter dari titik asal sepanjang sumbu x, lalu belok kiri dan berjalan sejajar dengan sumbu mereka empat meter ke dalam ruangan. Koordinat Cartesian dari titik di atas kepala Anda adalah (2,4,5).
Misalnya, notasi (2,4,5) sesuai dengan nilai X2, Y4, dan Z5. Lihat Gambar 8.
3 Dimensi
Koordinat kartesius dapat digunakan untuk mencari titik dalam 3 dimensi seperti pada contoh ini:

Gambar 9. Intinya(2, 4, 5 ) ditampilkan dalam koordinat kartesius tiga dimensi.
Kuadran
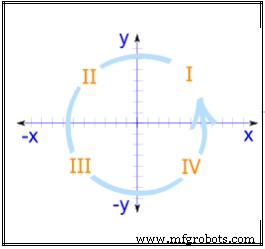
Sumbu koordinat membagi bidang menjadi empat bagian, yang disebut kuadran (Lihat Gambar 9). Kuadran adalah angka berlawanan arah jarum jam, dimulai dari kanan atas, berlabel I, II, III dan IV dengan penunjukan sumbu seperti yang ditunjukkan pada ilustrasi di bawah ini.
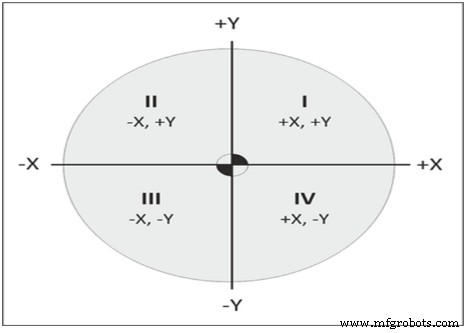
Gambar 10
Empat Kuadran:
Saat kita memasukkan nilai negatif, sumbu x dan y membagi ruang menjadi 4 bagian:
Kuadran I, II, III dan IV
(Mereka diberi nomor berlawanan arah jarum jam)

Dalam Kuadran I:x dan y keduanya positif
InQuadrant II :x negatif(y masih positif)
Dalam Kuadran III :x dan y keduanya negatif
Dalam Kuadran IV :x positif lagi, sedangkan y negatif
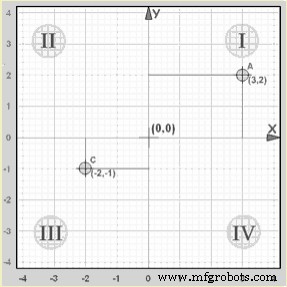
| Kuadran | X (Horisontal) | Y (Vertikal) | Contoh |
| Saya | Positif | Positif | (3,2) |
| II | Negatif | Positif | (-5, 2) |
| III | Negatif | Negatif | (-2, -1) |
| IV | Positif | Negatif | (2, -5) |
Contoh:Titik “A” (3,2) adalah 3 satuan di sepanjang sumbu x, dan 2 satuan di atas sumbu y.
Baik x maupun y keduanya positif, sehingga titik tersebut berada di “Kuadran I”
Contoh:Titik “C” (-2,-1) adalah 2 satuan sepanjang sumbu x dalam arah negatif, dan 1 satuan di bawah sumbu y dalam arah negatif.
Baik x maupun y keduanya negatif, sehingga titik tersebut berada di “Kuadran III”
Dimensi:1, 2, 3, dan lainnya …
1. Garis Bilangan Riil hanya dapat digunakan:
- kiri-kanan
- jadi posisi apapun hanya membutuhkan satu nomor
2. Koordinat kartesius dapat berupa:
- kiri-kanan, dan
- naik-turun
- jadi setiap posisi membutuhkan dua angka
3. 3 dimensi
- kiri-kanan,
- naik-turun, dan
- maju-mundur
UJI UNIT
1. Apa itu CNC?
2. Jelaskan sistem koordinat kartesius.
3. Apa Asal Mulanya?
4. Garis horizontal disebut apa?
5. Garis Vertikal disebut apa?
6. Gambarkan garis bilangan real.
7. Menjelaskan Absis dan Ordinasi.
8. Apa representasi dari tiga sumbu sistem koordinat kartesius tiga dimensi.
9. Sumbu koordinat membagi bidang menjadi empat bagian, disebut apa?
10. Di Kuadran IV, sumbu X dan sumbu Y adalah apa?








 Gambar 5Sumbu X dan Y:
Gambar 5Sumbu X dan Y:  Garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y; kedua garis berjalan melalui nol(Asal, (0,0)).
Garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y; kedua garis berjalan melalui nol(Asal, (0,0)).  Garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y; kedua garis melewati nol(Asal, (0,0)). Letakkan keduanya pada grafik …Lihat gambar 6
Garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y; kedua garis melewati nol(Asal, (0,0)). Letakkan keduanya pada grafik …Lihat gambar 6 
 Titik(6,4)adalah
Titik(6,4)adalah 


