Algoritma Pengoptimalan Variabel Ortogonal yang Efisien untuk Sistem Komunikasi
Artikel ini membahas algoritma untuk menemukan titik penyesuaian optimal dalam ruang dua dimensi dengan vektor input ortogonal. Algoritme menyelesaikan persamaan untuk lingkaran berpotongan berdasarkan titik data terukur.
Beberapa metrik kinerja sistem utama ditentukan oleh parameter input ortogonal yang sesuai dengan amplitudo dan fase; dua contoh adalah feedthrough pembawa modulator quadrature dan penekanan sideband. Parameter ini ditingkatkan dengan mengoptimalkan keseimbangan offset DC serta keseimbangan amplitudo dan fase antara input pita dasar kuadratur dari modulator.
Karena menemukan penyesuaian optimal dari parameter ini bukanlah tugas sepele mengingat ruang dua dimensi, dalam artikel ini saya akan membahas algoritma Python untuk menemukan titik penyesuaian optimal dalam ruang dua dimensi dengan vektor input ortogonal. Algoritme memecahkan persamaan untuk lingkaran yang berpotongan berdasarkan titik data terukur dan menemukan titik optimal hanya dalam empat iterasi. Untuk mencontohkan teknik ini, saya menggunakan Texas Instruments (TI) AFE7070 terintegrasi digital-to-analog converter (DAC) ditambah parameter feedthrough pembawa modulator quadrature.
Mengoptimalkan Emisi Palsu
Sistem komunikasi berusaha untuk meminimalkan emisi palsu. Beberapa emisi palsu ini berasal dari ketidakcocokan sinyal input ortogonal. Misalnya, ketidakcocokan offset DC dan ketidakseimbangan amplitudo/fase masing-masing akan mempengaruhi feedthrough carrier dan parameter penekanan sideband, dalam modulator kuadratur analog. Menyesuaikan variabel input ke setpoint optimal meminimalkan output palsu.
Gambar 1 merepresentasikan parameter terukur sebagai magnitudo (r) vektor dari titik yang dioptimalkan, [x0,y0], ke titik sebenarnya pada bidang dua dimensi. Nilai parameter dibatasi oleh [0,1], sebuah lingkaran satuan. Angka 0 menunjukkan pembatalan total atau tidak ada sinyal dan angka 1 menunjukkan tidak ada pembatalan atau sinyal penuh. Dalam skala desibel, fungsi dibatasi oleh [-inf,0]. Lingkaran dengan jari-jari r mewakili semua kemungkinan titik x,y yang mencapai besaran yang sama.
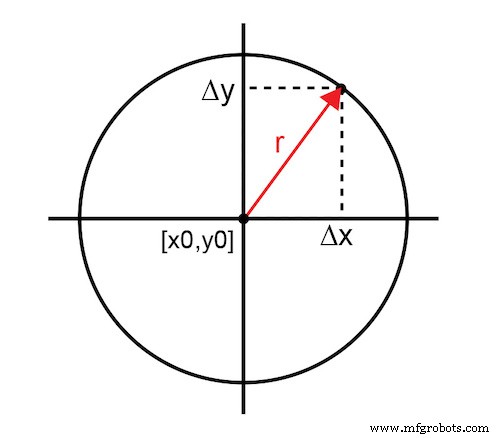
Gambar 1. Vektor dari titik yang dioptimalkan ke titik sebenarnya
Persamaan 1 mewakili fungsi dalam bentuk paling sederhana:
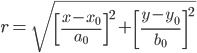 (1)
(1)
Konstanta [a0,b0] mewakili faktor normalisasi yang bergantung pada sistem untuk menjaga hasil maksimum kurang dari 1. Secara teknis, Persamaan 1 menggambarkan elips, karena faktor penskalaan untuk setiap variabel independen tidak harus sama. Untuk mempermudah dalam analisis ini, a0 sama dengan b0 sehingga kurva benar-benar lingkaran.
Tujuannya adalah untuk menemukan titik optimal [x0,y0] yang meminimalkan parameter pengukuran (r) secepat mungkin. Menemukan titik itu secara efisien dengan parameter input yang bervariasi secara statistik itu menantang. Pendekatan berburu dan mematuk tradisional menggunakan percobaan berturut-turut untuk mempersempit ke titik optimal. Meskipun ini menghasilkan solusi yang diinginkan, dibutuhkan terlalu banyak iterasi ketika waktu konvergensi sangat penting, sehingga memerlukan metode baru.
Lingkaran Berpotongan
Idealnya, tepat tiga iterasi pengukuran menggunakan lingkaran berpotongan menentukan titik optimal. Hasil pengukuran pertama pada titik input arbitrer [x1,y1] mendefinisikan kemungkinan tak terbatas untuk titik optimal yang diwakili oleh lingkaran A dengan jari-jari r1. Menambahkan titik data kedua menghasilkan kumpulan data tak terbatas lainnya yang diwakili oleh lingkaran B; namun, perpotongan dua lingkaran mempersempit solusi menjadi dua titik. Titik data ketiga dan lingkaran C yang sesuai memberikan kurva ketiga di mana hanya ada satu titik perpotongan timbal balik. Titik potong tersebut merupakan titik optimal. Gambar 2 menunjukkan perkembangan lingkaran berpotongan yang berpuncak pada titik optimal definitif.
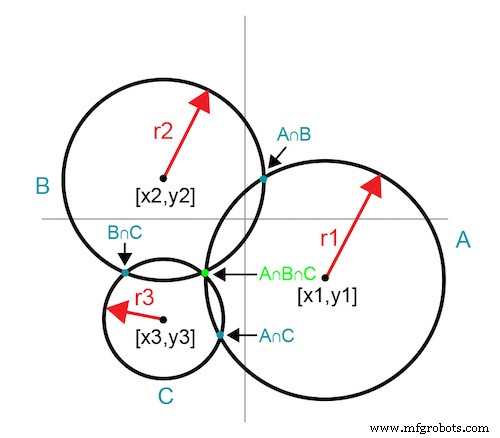
Gambar 2. Lingkaran yang berpotongan mengungkapkan titik persimpangan yang sama
Teknik ini mengungkapkan titik optimal dalam tepat tiga iterasi. Iterasi keempat mengukur titik optimal untuk mengonfirmasi dan mendokumentasikan hasilnya.
Gambar 3 mengilustrasikan teknik untuk menghilangkan satu iterasi dengan menggunakan informasi batas yang diketahui secara empiris dalam bidang xy. Pilih titik awal pada salah satu titik batas sehingga kurva pertama (A) adalah busur 90 derajat. Pilih titik kedua pada busur pertama dengan bergerak baik dalam arah x atau y.
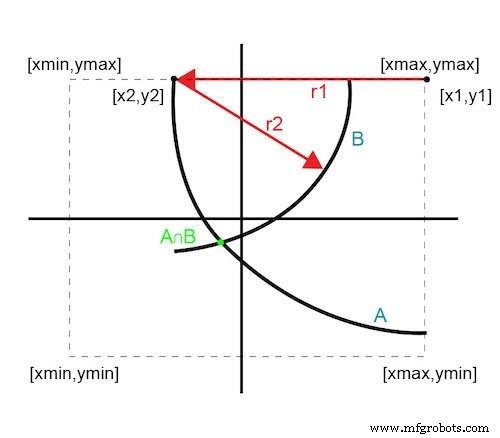
Gambar 3. Solusi dua iterasi
Karena titik kedua masih di tepi batas, kurvanya adalah busur sub-180 derajat. Perpotongan kedua kurva ini memberikan satu titik optimal. Pendekatan ini mengungkapkan titik optimal hanya dalam dua iterasi dan menegaskannya dengan tiga.
Pendekatan Lingkaran Berturut-turut
Solusi optimal tergantung pada keakuratan persamaan matematika. Dalam situasi pengukuran nyata, beberapa asumsi atau kesalahan akan mempengaruhi hasil. Sinyal yang diukur sangat kecil; kebisingan dan toleransi pengukuran menimbulkan kesalahan. Menggunakan lingkaran sempurna alih-alih elips menimbulkan beberapa ketidakpastian. Asumsi faktor penskalaan yang diperlukan untuk menyelesaikan banyak persamaan juga menimbulkan ketidakpastian. Kesalahan dan asumsi ini diterjemahkan menjadi ketidakjelasan di kurva.
Gambar 4 mengilustrasikan bagaimana kurva fuzzy tidak menjamin titik perpotongan yang tepat; sebaliknya, mereka mendefinisikan area konvergensi.
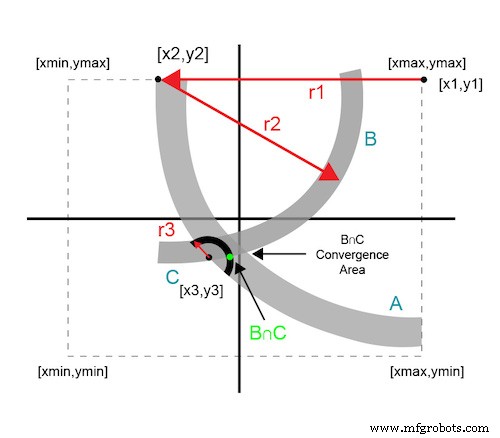
Gambar 4. Perkiraan persimpangan lingkaran yang berurutan
Setiap titik data tambahan menggunakan data dari iterasi sebelumnya. Lingkaran yang berurutan menyatu ke area solusi yang berada dalam ambang minimum sistem.
Contoh Pengukuran
Contoh ini menggunakan AFE7070 DAC dan mengoptimalkan parameter feedthrough carrier. AFE7070 adalah platform yang nyaman, karena DAC dan modulator terintegrasi. Ketidakseimbangan offset DC pada input quadrature modulator menentukan kinerja feedthrough pembawa. AFE7070 memiliki fitur penyetelan digital internal untuk mengontrol keseimbangan offset DC dengan cermat. Tidak perlu banyak; resolusinya dalam skala mikrovolt.
Parameter x,y sebagai contoh adalah nilai langkah digital integer yang mengontrol level DC pada input kuadratur. Pengambilan sampel statistik perangkat sebelumnya memberikan batas x,y dari variabel input serta tabel langkah yang digunakan dalam perhitungan. Tabel langkah memberikan "konversi" dari umpan pembawa terukur dalam miliwatt desibel ke faktor delta-x (atau delta-y).
Nilai terukur yang tinggi (atau dengan kata lain, buruk) berarti pengaturannya jauh dan membutuhkan delta yang lebih besar untuk mencapai titik optimal. Sebaliknya, nilai yang rendah berarti setpoint sudah dekat dan perlu koreksi kecil. Sedikit "pekerjaan rumah" ini diperlukan untuk memastikan bahwa poin tebakan awal tidak terlalu jauh, dan untuk mengurangi waktu iterasi seminimal mungkin.
Gambar 5 menunjukkan algoritma Python yang menemukan variabel input optimal dalam empat iterasi atau kurang.

Gambar 5. Algoritme pengoptimalan python
Fungsi "Get_r" dan "GetCFi" adalah pengukuran khusus perangkat. Saya telah menghilangkan kode untuk singkatnya, karena tidak penting untuk mendemonstrasikan algoritme pengoptimalan. Dalam aplikasi Anda, fungsi-fungsi ini berkaitan dengan pemrograman dan pengukuran parameter perangkat di sistem Anda.
Kesimpulan
Untuk AFE7070 DAC, dalam banyak kasus, algoritme mengoptimalkan umpan pembawa dalam tiga iterasi dan dalam waktu kurang dari 1,7 detik, terutama dipagari oleh penganalisis spektrum waktu penyelesaian dan penyapuan. Metode langkah sebelumnya membutuhkan hampir 20 iterasi dan lebih dari 20 detik untuk diselesaikan. Algoritma ini mewakili peningkatan kecepatan lebih dari 10 kali dibandingkan dengan pendekatan tradisional. Parameter sistem komunikasi lain yang bergantung pada variabel input ortogonal penguatan dan fase juga dapat menggunakan algoritme ini untuk secara efisien memasukkan solusi optimal.
Artikel Industri adalah bentuk konten yang memungkinkan mitra industri untuk berbagi berita, pesan, dan teknologi yang bermanfaat dengan pembaca All About Circuits dengan cara yang tidak sesuai dengan konten editorial. Semua Artikel Industri tunduk pada pedoman editorial yang ketat dengan tujuan menawarkan kepada pembaca berita, keahlian teknis, atau cerita yang bermanfaat. Sudut pandang dan pendapat yang diungkapkan dalam Artikel Industri adalah dari mitra dan belum tentu dari All About Circuits atau penulisnya.





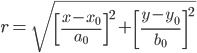 (1)
(1)


