Untuk referensi, bagian ini memperkenalkan terminologi yang digunakan dalam beberapa teks untuk menggambarkan minterms dan maxterms yang ditetapkan untuk peta Karnaugh. Jika tidak, tidak ada materi baru di sini.
(sigma) menunjukkan jumlah dan huruf kecil "m" menunjukkan minterms. m menunjukkan jumlah minterms. Contoh berikut ditinjau kembali untuk mengilustrasikan poin kami. Alih-alih deskripsi persamaan Boolean dari logika yang tidak disederhanakan, kami mencantumkan mintermnya.
f(A,B,C,D) =m(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15) atau f(A,B,C,D) =(m1 ,m2 ,m3 ,m4 ,m5 ,m7 ,m8 ,m9 ,m11 ,m12 ,m13 ,m15 )
Angka-angka menunjukkan lokasi sel, atau alamat, dalam peta Karnaugh seperti yang ditunjukkan di bawah ini. Ini tentu saja merupakan cara yang ringkas untuk mendeskripsikan daftar minterm atau sel dalam peta-K.
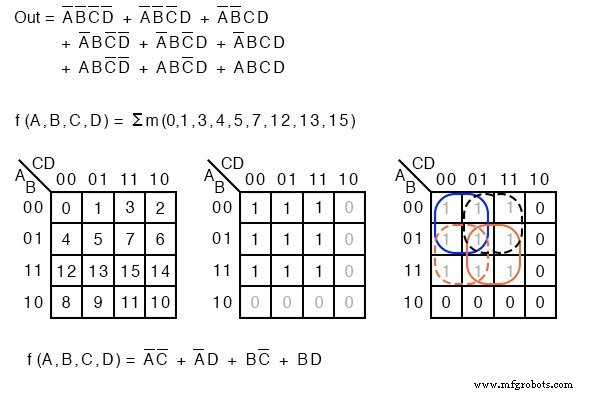
Solusi Sum-Of-Products tidak terpengaruh oleh terminologi baru. Minterm, 1 s, di peta telah dikelompokkan seperti biasa dan solusi Sum-OF-Products ditulis.
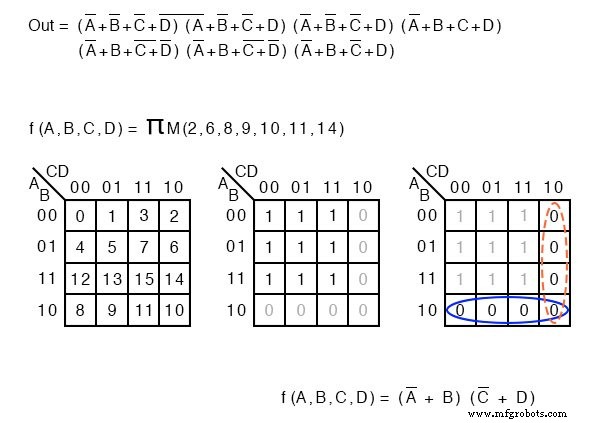
Di bawah ini, kami menunjukkan terminologi untuk menggambarkan daftar maxterms. Produk ditunjukkan oleh bahasa Yunani (pi), dan huruf besar "M" menunjukkan maxterms. M menunjukkan produk dari maxterms. Contoh yang sama mengilustrasikan poin kami.
Deskripsi persamaan Boolean dari logika yang tidak disederhanakan, diganti dengan daftar maxterms.
f(A,B,C,D) =M(2, 6, 8, 9, 10, 11, 14) atau f(A,B,C,D) =(M2 , M6 , M8 , M9 , M10 , M11 , M14 )
Sekali lagi, angka menunjukkan lokasi alamat sel K-map. Untuk maxterms ini adalah lokasi 0 s, seperti yang ditunjukkan di bawah ini. Solusi Product-OF-Sums diselesaikan dengan cara biasa.
$$Keluar =(A + B + \bar{C} + D)(A + \bar{B} + \bar{C} + D) + (\bar{A} + B + C + \bar{D }) + (\bar{A} + B + \bar{C} + D)$$
$$(\bar{A} + B + \bar{C} +\bar{D})(\bar{A} + \bar{B} + \bar{C} + D)$$
LEMBAR KERJA TERKAIT:
Teknologi Industri
Pengobatan modern bergantung pada berbagai alat dan instrumen yang berbeda. Mulai dari pipa fleksibel hingga kain kasa hingga klem logam tahan lama dan kaki palsu, perangkat ini memiliki banyak bentuk. Sama seperti FDA yang mengatur bahan mana yang dapat digunakan dalam rantai pasokan makanan dan ob
Industri permesinan presisi berkumpul secara langsung untuk pertama kalinya dalam lebih dari dua tahun di Precision Machining Technology Show (PMTS) 2021 yang ditetapkan pada 10-12 Agustus 2021, di Cleveland, Ohio, di Huntington Convention Center. Seiring dengan momentum ekonomi yang terus meningka
Pada akhir abad ke-15, Leonardo Da Vinci membuat sketsa rolling mill sederhana yang menunjukkan kemungkinan membengkokkan lembaran logam. Namun, baru pada tahun 1590 sketsa ini menjadi kenyataan ketika pekerja logam mulai menggunakan dua silinder berat untuk menekan logam, mengubah ketebalan dan ben
Saat ini, istilah keramik terdiri dari bahan yang jauh lebih luas, termasuk oksida logam, nitrida, dan karbida. Bahan-bahan ini digunakan di area aplikasi mulai dari barang-barang rumah tangga hingga alat berperforma tinggi untuk keperluan industri. Selain kekerasannya yang hebat , keramik juga tah
